Методические указания по выполнению задания
Статистический анализ совокупности (включает темы №№ 3, 4, 5, 6, 7).
Задание должно быть выполнено на основе информации, приведенной в Приложении 1 «Основные технико-экономические показатели работы предприятия». Для этого:
1. По данным приложения 1 следует произвести методом случайного бесповторного отбора выборку 30 предприятий по одному из показателей работы. Показатели распределены между студентами в зависимости от начальной буквы их фамилий:
| номер колонки табл.1 прилож.1 | начальная буква фамилии студента | номер колонки табл.1прилож.1 | начальная буква фамилии студента |
| А, Б | М | ||
| В, Г | Н, Р | ||
| Д, Е | П | ||
| Ж, З | Щ, Ю | ||
| И, Я | У, Ф, Х | ||
| К | Ц, Ч, Ш | ||
| Л, О | С, Т |
Отбор производится следующим образом: из таблицы случайных чисел (Таблица 1 Приложение 2) наугад выберите колонку случайных чисел и выпишите из них 30 чисел, т.к. в выборке должны встречаться только двузначные числа, то в указанных случайных числах можно отбросить или две первые цифры, или две последние, или первую и последнюю. Например, случайное число 2056, отбросим две первые цифры, остается 56, следовательно, из исходных данных необходимо отобрать предприятие с номером 56. После этого из генеральной совокупности (прил.1) отберите 30 единиц с номерами, которые попали в выборку.
2. По выборочной совокупности рассмотрите закономерность распределения исследуемого признака. Для этого:
а. постройте интервальный ряд распределения и изобразите его графически в виде гистограммы, полигона и кумуляты;
б. рассчитайте характеристики распределения: среднюю арифметическую, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации и коэффициенты асимметрии и эксцесса. Проанализируйте исчисленные показатели и сделайте выводы.
3. По кривым распределения произведите выравнивание эмпирического ряда распределения. Для этого рассмотрите уравнение нормальной кривой, рассчитайте ординаты и теоретические частоты нормального распределения. Постройте график. Сделайте выводы.
4. Сделайте проверку гипотезы о соответствии эмпирического распределения закону нормального распределения при помощи критерия c2 (хи-квадрат) К.Пирсона. Сделайте заключение о случайности или существенности расхождений эмпирических и теоретических частот.
5. С вероятностью 0,954 (confidence probability) определите ошибку выборки средней и границы генеральной средней. Сделайте выводы.
Методические указания по выполнению задания
Для выравнивания рядов распределения применяют кривую нормального распределения, логнормальную кривую, распределение Пуассона и др.
Уравнение нормальной кривой имеет следующий вид:
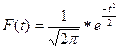
где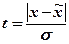 
– нормированное отклонение
Кривые нормального распределения строятся по двум параметрам - x и s.
Для определения ординат (F(t)) и теоретических частот нормального распределения (f’) постройте следующую расчетную таблицу (табл.2). Для определения F(t) используйте таблицу 2 приложения 2, в которой в заголовках строк указаны целые и десятые доли значения t, а в заголовках столбцов указаны сотые доли t. Например, чтобы определить значение F(t) для t=1,74, необходимо, в заголовках строк найти значение 1,7, а в заголовках столбиков – значение 4. На пересечении строки и столбца располагается значение F(t).
Таблица 2
| рассматриваемый признак (середина интервала) (xi) | число предприятий (fi) | 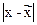 | 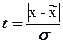 | F(t) | теоретические частоты (число предприятий)  |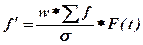
| ......... | ........... | ........... | ............. | ............ | ............. |
| сумма | ........... | ........... | ............ | ............ | ............ |
Для проверки гипотезы о соответствии фактического распределения закону нормального распределения (теоретическому распределению) применяется критерий согласия c2 (хи - квадрат) К. Пирсона.
Расчетное значение c2 (хи-квадрат) определяется по формуле:
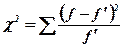
Теоретическое значение c2табл (хи-квадрат) определяется по таблицам критических значений (таблица 3 приложения 2) в зависимости от числа степеней свободы k:
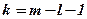
где m – число интервальных групп ряда распределений;
l – число параметров кривой нормального распределения при заданной доверительной вероятности P.
Так как вы рассматриваете выборочную совокупность, то целесообразно вычислить ошибку выборки и определить границы генеральной средней с заданной вероятностью.
Предельная ошибка выборки (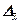 
) для бесповторного случайного отбора определяется по формуле:
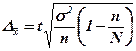
где t – коэффициент доверия (confidence coefficient), определенный таблично по доверительной вероятности (Р), при этом для Р=0.997 коэффициент доверия t=3, для Р=0.954 t=2, для Р=0.683 t=1;
n – численность выборки (30);
N – численность генеральной совокупности (100).
Границы генеральной средней (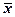 
) определяются по формуле:
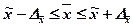
ПРИЛОЖЕНИЕ 1
| № предприятия | Продукция, млрд.руб. | Численность ППП, чел. | Среднегодовая стоимость ОФ, млрд.руб. | Потери рабочего времени на 1 рабочего, чел.-дн. | Износ ОФ, % | Фондоотдача, руб. | Фондовооруженность труда, млрд.руб. | Электровооруженность, 1чел.-ч., кВт.ч. | Техническая вооруженность 1 рабочего, млн.руб. | Выработка товарной продукции на 1 работающего, млн.руб. | Удельный вес активной части ОФ, % | Балансовая прибыль, млн.руб. | Прибыль от реализации продукции, млн.руб. | |
| 1 работающего | 1 рабочего | |||||||||||||
| А | ||||||||||||||
| 1,32 | 0,22 | 12,2 | 46,5 | 5,97 | 0,44 | 0,52 | 63,4 | 18,2 | 2,6 | 44,3 | 3,31 | 3,27 | ||
| 3,32 | 0,54 | 51,5 | 6,15 | 5,29 | 0,62 | 74,5 | 21,5 | 32,5 | 45,5 | 1,03 | 1,03 | |||
| 9,78 | 0,14 | 11,6 | 48,1 | 70,87 | 0,33 | 0,41 | 69,5 | 12,2 | 23,3 | 35,9 | 1,90 | 1,87 | ||
| 3,92 | 0,54 | 10,2 | 54,5 | 7,22 | 0,56 | 0,65 | 98,5 | 26,1 | 4,0 | 51,9 | 1,66 | 1,64 | ||
| 2,85 | 0,48 | 11,2 | 44,1 | 5,89 | 3,10 | 0,37 | 48,1 | 18,9 | 18,3 | 55,5 | 2,16 | 2,63 | ||
| 4,78 | 0,34 | 13,8 | 51,1 | 14,10 | 1,22 | 0,15 | 19,1 | 4,9 | 17,2 | 38,7 | 1,95 | 0,92 | ||
| 8,76 | 0,92 | 12,6 | 49,8 | 9,53 | 1,34 | 0,16 | 12,9 | 5,6 | 12,8 | 40,5 | 1,60 | 1,54 | ||
| 2,89 | 0,69 | 15,4 | 70,4 | 4,18 | 1,27 | 0,15 | 16,9 | 5,3 | 5,3 | 48,9 | 1,17 | 0,98 | ||
| 2,37 | 0,27 | 14,1 | 34,4 | 8,64 | 0,78 | 0,08 | 13,9 | 3,2 | 6,7 | 43,3 | 1,82 | 1,12 | ||
| 1,06 | 0,12 | 15,7 | 59,9 | 8,87 | 0,69 | 0,09 | 14,4 | 3,5 | 6,1 | 39,8 | 2,13 | 1,13 | ||
| 1,04 | 0,29 | 11,5 | 40,8 | 3,62 | 0,84 | 0,99 | 83,1 | 24,2 | 3,0 | 37,6 | 1,09 | 1,09 | ||
| 5,50 | 1,64 | 16,1 | 25,5 | 3,36 | 6,47 | 0,77 | 65,5 | 19,9 | 21,7 | 32,2 | 3,55 | 2,94 | ||
| 8,21 | 0,27 | 14,7 | 37,3 | 30,18 | 0,75 | 0,92 | 82,4 | 26,4 | 22,6 | 34,8 | 1,76 | 1,43 | ||
| 8,91 | 0,78 | 51,9 | 11,49 | 1,74 | 0,21 | 30,5 | 10,8 | 19,9 | 59,3 | 1,14 | 1,08 | |||
| 9,46 | 0,86 | 12,4 | 49,8 | 10,98 | 1,73 | 0,2 | 35,9 | 12,1 | 19,0 | 60,9 | 1,19 | 1,09 | ||
| 3,34 | 0,83 | 13,3 | 32,7 | 4,03 | 2,28 | 0,31 | 6,6 | 6,5 | 9,2 | 28,1 | 1,88 | 0,89 | ||
| 1,40 | 0,20 | 11,2 | 44,8 | 6,91 | 0,36 | 0,43 | 76,5 | 2,5 | 53,5 | 2,51 | 2,52 | |||
| 6,17 | 1,28 | 10,8 | 47,6 | 4,84 | 1,91 | 0,22 | 31,9 | 8,1 | 9,2 | 45,8 | 1,85 | 1,83 | ||
| 1,94 | 0,22 | 16,8 | 8,71 | 2,86 | 0,15 | 31,5 | 6,4 | 24,9 | 61,7 | 1,91 | 1,49 | |||
| 1,89 | 0,33 | 10,6 | 34,6 | 5,72 | 3,45 | 0,76 | 167,9 | 38,9 | 19,7 | 54,7 | 4,08 | 4,05 | ||
| 2,12 | 0,56 | 11,6 | 32,2 | 3,76 | 0,88 | 1,06 | 120,3 | 34,8 | 3,3 | 43,9 | 2,66 | 2,76 | ||
| 1,40 | 0,15 | 10,6 | 9,39 | 1,66 | 0,45 | 141,5 | 25,6 | 15,5 | 63,5 | 3,20 | 3,21 | |||
| 5,44 | 2,20 | 8,7 | 67,1 | 2,47 | 91,63 | 0,21 | 28,8 | 10,5 | 226,7 | 52,8 | 4,80 | 4,58 | ||
| 6,18 | 4,57 | 9,6 | 62,2 | 1,35 | 16,44 | 0,19 | 29,6 | 8,6 | 22,2 | 53,5 | 1,61 | 1,62 | ||
| 1,13 | 0,36 | 12,2 | 45,8 | 3,11 | 3,67 | 0,15 | 11,5 | 11,4 | 27,5 | 2,12 | 2,11 | |||
| 6,71 | 0,86 | 6,9 | 54,5 | 7,84 | 9,62 | 0,26 | 13,1 | 75,4 | 1,45 | 1,48 | ||||
| 8,37 | 5,15 | 10,3 | 27,2 | 1,62 | 12,72 | 0,16 | 3,3 | 1,6 | 20,7 | 2,12 | 1,99 | |||
| 3,62 | 1,49 | 13,1 | 46,1 | 2,43 | 13,06 | 0,15 | 20,8 | 7,5 | 31,8 | 51,6 | 2,85 | 2,85 | ||
| 7,48 | 0,95 | 14,9 | 50,1 | 7,88 | 7,36 | 0,09 | 9,8 | 2,5 | 57,9 | 34,2 | 1,10 | 1,46 | ||
| 5,42 | 2,23 | 11,8 | 37,7 | 2,43 | 7,26 | 0,09 | 5,2 | 4,4 | 17,7 | 38,6 | 2,01 | 1,10 | ||
| 1,01 | 0,52 | 8,8 | 36,3 | 1,95 | 10,38 | 0,12 | 14,5 | 7,7 | 20,3 | 71,9 | 2,18 | 1,18 | ||
| 4,75 | 0,21 | 58,6 | 22,85 | 3,92 | 0,46 | 139,4 | 29,7 | 89,7 | 65,6 | 4,02 | 3,97 | |||
| 1,18 | 0,14 | 10,9 | 48,6 | 8,38 | 2,88 | 0,33 | 61,6 | 17,9 | 24,1 | 56,4 | 1,15 | 1,26 | ||
| 2,60 | 2,03 | 13,5 | 62,7 | 1,28 | 10,52 | 0,12 | 18,9 | 13,5 | 52,1 | 1,29 | 1,26 | |||
| 6,75 | 0,71 | 12,6 | 55,4 | 9,56 | 2,57 | 0,3 | 60,2 | 16,4 | 24,5 | 57,2 | 1,22 | 1,16 | ||
| 2,73 | 0,31 | 15,1 | 41,8 | 8,75 | 2,07 | 0,25 | 5,1 | 17,9 | 18,1 | 54,2 | 1,96 | 0,96 | ||
| 9,80 | 1,70 | 60,4 | 5,77 | 4,47 | 0,53 | 75,9 | 27,2 | 25,8 | 73,4 | 2,63 | 1,66 | |||
| 1,10 | 0,54 | 17,8 | 60,5 | 2,03 | 0,78 | 0,09 | 15,5 | 4,5 | 1,6 | 55,9 | 1,25 | 0,99 | ||
| 2,02 | 0,34 | 13,9 | 58,7 | 5,97 | 0,71 | 0,08 | 3,6 | 4,2 | 50,8 | 1,81 | 1,64 | |||
| 2,37 | 1,97 | 35,4 | 1,20 | 3,77 | 0,44 | 37,3 | 4,5 | 2,01 | 2,04 | |||||
| 6,22 | 3,04 | 2,05 | 10,53 | 0,13 | 13,9 | 21,5 | 58,5 | 1,77 | 1,13 | |||||
| 8,86 | 1,62 | 40,8 | 5,46 | 3,69 | 0,42 | 55,3 | 19,3 | 20,1 | 51,6 | 1,61 | 1,63 | |||
| 3,12 | 2,37 | 13,8 | 26,3 | 1,32 | 11,29 | 0,14 | 5,7 | 3,8 | 14,8 | 32,6 | 1,26 | 1,25 | ||
| 1,86 | 0,80 | 9,4 | 19,4 | 2,32 | 1,48 | 1,75 | 87,2 | 66,4 | 3,4 | 42,8 | 2,79 | 1,83 | ||
| 5,63 | 0,48 | 17,5 | 63,6 | 11,72 | 3,10 | 0,36 | 56,2 | 17,1 | 36,3 | 57,8 | 1,55 | 1,78 | ||
| 1,92 | 0,19 | 10,22 | 2,00 | 0,24 | 27,6 | 12,3 | 20,4 | 58,3 | 3,00 | 2,86 | ||||
| 1,66 | 0,20 | 64,4 | 8,45 | 2,25 | 0,19 | 31,1 | 10,4 | 19,0 | 61,6 | 3,57 | 2,73 | |||
| 2,03 | 0,34 | 11,8 | 46,4 | 6,05 | 0,41 | 0,46 | 60,5 | 20,4 | 2,5 | 54,1 | 4,35 | 4,24 | ||
| 1,34 | 0,98 | 9,5 | 45,9 | 1,36 | 21,87 | 0,26 | 33,5 | 13,8 | 29,8 | 55,8 | 4,70 | 4,74 | ||
| 3,12 | 0,44 | 12,4 | 7,05 | 3,16 | 0,37 | 35,1 | 14,6 | 22,3 | 47,2 | 9,92 | 9,47 | |||
| 3,01 | 0,34 | 10,8 | 42,4 | 8,83 | 2,17 | 0,25 | 26,5 | 8,1 | 19,2 | 37,3 | 5,15 | 5,21 | ||
| 1,48 | 0,64 | 13,4 | 48,9 | 2,31 | 6,68 | 0,08 | 4,4 | 15,4 | 42,5 | 3,17 | 3,14 | |||
| 4,11 | 3,92 | 9,1 | 43,7 | 1,05 | 21,08 | 0,24 | 24,9 | 9,5 | 22,1 | 42,9 | 2,99 | 2,99 | ||
| 6,92 | 8,07 | 12,9 | 32,9 | 0,86 | 18,30 | 0,21 | 13,2 | 11,5 | 15,7 | 56,5 | 2,86 | 2,91 | ||
| 1,02 | 0,67 | 11,2 | 43,4 | 1,52 | 8,39 | 0,09 | 14,9 | 3,1 | 12,8 | 40,2 | 3,08 | 3,09 | ||
| 7,53 | 2,81 | 14,1 | 33,6 | 2,68 | 10,82 | 0,13 | 2,4 | 8,5 | 29,0 | 56,8 | 1,28 | 1,27 | ||
| 4,70 | 1,19 | 17,3 | 52,1 | 3,96 | 10,68 | 0,14 | 5,8 | 9,7 | 42,4 | 73,8 | 2,86 | 2,89 | ||
| 5,73 | 6,33 | 35,7 | 0,91 | 55,50 | 0,66 | 50,4 | 34,7 | 50,3 | 1,53 | 1,55 | ||||
| 3,29 | 1,61 | 14,9 | 39,5 | 2,04 | 1,87 | 0,23 | 4,9 | 3,2 | 3,8 | 47,7 | 1,79 | 1,80 | ||
| 1,81 | 0,15 | 9,2 | 53,5 | 12,33 | 0,19 | 0,23 | 25,9 | 13,4 | 2,4 | 63,6 | 2,24 | 1,25 | ||
| 2,96 | 0,28 | 13,7 | 55,9 | 10,72 | 2,76 | 0,33 | 43,5 | 20,2 | 29,6 | 63,1 | 3,45 | 3,44 | ||
| 2,26 | 0,24 | 10,3 | 17,5 | 9,46 | 1,42 | 0,18 | 3,1 | 4,7 | 13,5 | 31,7 | 2,35 | 2,33 | ||
| 1,88 | 0,25 | 19,1 | 53,9 | 7,51 | 3,25 | 0,04 | 0,6 | 2,2 | 24,4 | 56,8 | 3,02 | 3,02 | ||
| 4,94 | 0,85 | 13,1 | 63,8 | 5,80 | 3,40 | 0,4 | 43,1 | 18,1 | 19,7 | 51,4 | 2,63 | 2,63 | ||
| 6,90 | 1,26 | 44,9 | 5,47 | 8,14 | 0,1 | 0,7 | 44,5 | 52,2 | 2,17 | 2,17 | ||||
| 3,19 | 0,48 | 12,7 | 43,2 | 6,67 | 1,08 | 0,01 | 0,2 | 0,6 | 7,2 | 51,8 | 4,01 | 4,01 | ||
| 5,38 | 3,67 | 5,4 | 52,1 | 1,47 | 12,02 | 0,14 | 6,6 | 5,9 | 17,7 | 47,8 | 2,12 | 2,12 | ||
| 1,77 | 1,63 | 14,6 | 20,3 | 1,09 | 1,86 | 0,23 | 4,8 | 8,4 | 2,0 | 39,1 | 2,47 | 2,47 | ||
| 2,41 | 0,28 | 20,5 | 63,3 | 8,55 | 2,47 | 0,3 | 48,7 | 16,5 | 21,1 | 65,6 | 2,53 | 2,53 | ||
| 1,66 | 0,82 | 13,4 | 37,5 | 2,02 | 11,58 | 0,15 | 17,8 | 5,6 | 23,4 | 42,5 | 2,54 | 2,54 | ||
| 6,93 | 1,48 | 14,1 | 40,1 | 4,68 | 9,14 | 0,12 | 3,3 | 42,7 | 32,9 | 2,21 | 2,22 | |||
| 5,39 | 3,80 | 14,9 | 36,8 | 1,42 | 11,47 | 0,14 | 20,8 | 6,5 | 16,3 | 49,5 | 2,15 | 2,15 | ||
| 4,33 | 2,95 | 10,7 | 1,47 | 13,59 | 0,17 | 23,9 | 5,9 | 20,0 | 38,3 | 3,18 | 3,18 | |||
| 8,87 | 4,20 | 12,3 | 2,11 | 9,12 | 0,25 | 27,5 | 10,8 | 19,2 | 51,4 | 1,62 | 1,63 | |||
| 2,84 | 0,27 | 14,7 | 58,1 | 10,44 | 2,62 | 0,31 | 33,2 | 10,3 | 27,3 | 47,5 | 2,55 | 2,75 | ||
| 3,63 | 0,27 | 9,5 | 44,5 | 13,60 | 1,67 | 0,2 | 23,1 | 8,7 | 22,7 | 50,8 | 7,31 | 7,28 | ||
| 1,62 | 0,13 | 12,3 | 48,1 | 12,67 | 0,21 | 0,25 | 35,1 | 12,4 | 2,6 | 55,4 | 3,61 | 3,52 | ||
| 9,71 | 1,09 | 13,2 | 53,6 | 8,95 | 2,38 | 0,29 | 32,5 | 13,2 | 21,3 | 53,9 | 9,78 | 1,00 | ||
| 5,54 | 0,60 | 15,8 | 57,1 | 9,20 | 2,16 | 0,27 | 37,2 | 13,1 | 19,9 | 3,41 | 3,10 | |||
| 3,27 | 0,61 | 14,3 | 54,8 | 5,39 | 3,16 | 0,37 | 33,8 | 17,0 | 59,3 | 2,53 | 2,52 | |||
| 3,19 | 2,21 | 12,2 | 46,5 | 1,44 | 4,40 | 0,52 | 63,4 | 18,2 | 6,3 | 44,3 | 3,31 | 3,27 | ||
| 9,78 | 0,14 | 11,6 | 48,1 | 70,86 | 0,33 | 0,37 | 69,5 | 12,2 | 23,3 | 35,9 | 1,90 | 1,87 | ||
| 2,85 | 0,48 | 11,2 | 44,1 | 5,89 | 3,10 | 0,37 | 48,1 | 18,9 | 18,3 | 55,5 | 3,22 | 3,26 | ||
| 8,76 | 0,92 | 12,6 | 49,8 | 9,54 | 1,34 | 0,16 | 12,9 | 5,6 | 12,8 | 40,5 | 1,16 | 3,15 | ||
| 2,37 | 0,27 | 14,1 | 34,4 | 8,64 | 0,78 | 0,08 | 13,9 | 3,2 | 6,7 | 43,3 | 2,18 | 2,11 | ||
| 10,39 | 2,87 | 11,5 | 40,8 | 3,62 | 8,37 | 0,99 | 83,1 | 24,2 | 30,3 | 37,6 | 1,09 | 1,09 | ||
| 8,21 | 2,73 | 14,7 | 37,3 | 3,01 | 7,51 | 0,92 | 82,4 | 26,4 | 22,6 | 34,8 | 1,76 | 1,43 | ||
| 9,46 | 0,86 | 12,4 | 49,8 | 10,98 | 1,73 | 0,2 | 35,9 | 12,1 | 19,0 | 60,9 | 1,19 | 1,09 | ||
| 1,40 | 0,20 | 11,2 | 44,8 | 6,91 | 3,69 | 0,43 | 76,5 | 25,5 | 53,5 | 2,51 | 2,52 | |||
| 1,94 | 0,22 | 16,8 | 8,71 | 13,12 | 0,15 | 31,5 | 6,4 | 114,3 | 61,7 | 3,09 | 3,05 | |||
| 2,12 | 0,56 | 11,6 | 32,2 | 3,76 | 0,88 | 1,06 | 120,3 | 34,8 | 3,3 | 43,9 | 2,66 | 2,76 | ||
| 2,44 | 0,22 | 8,7 | 67,1 | 11,15 | 1,77 | 0,2 | 28,8 | 10,5 | 19,7 | 52,8 | 2,48 | 2,46 | ||
| 1,13 | 0,36 | 12,2 | 45,8 | 3,12 | 3,67 | 0,15 | 11,5 | 11,4 | 27,5 | 2,12 | 2,11 | |||
| 8,37 | 0,52 | 10,3 | 27,2 | 16,25 | 1,27 | 0,16 | 3,3 | 1,6 | 20,7 | 2,12 | 2,13 | |||
| 7,48 | 0,95 | 14,9 | 50,1 | 7,88 | 7,36 | 0,09 | 9,8 | 2,5 | 57,9 | 34,2 | 3,10 | 3,07 | ||
| 1,01 | 0,52 | 8,8 | 36,3 | 1,95 | 9,98 | 0,12 | 14,5 | 7,7 | 19,5 | 71,9 | 3,18 | 3,18 | ||
| 1,18 | 0,14 | 10,9 | 48,6 | 8,38 | 1,42 | 0,33 | 61,6 | 17,9 | 11,9 | 56,4 | 1,15 | 1,26 | ||
| 6,75 | 0,71 | 12,6 | 55,4 | 9,56 | 2,57 | 0,3 | 60,2 | 16,4 | 24,5 | 57,2 | 1,22 | 1,16 | ||
| 9,80 | 1,70 | 60,4 | 5,77 | 4,47 | 0,53 | 75,9 | 27,2 | 25,8 | 73,4 | 2,63 | 2,66 | |||
| 2,02 | 3,39 | 13,9 | 58,7 | 0,60 | 7,12 | 0,08 | 3,6 | 4,2 | 50,8 | 1,81 | 2,64 |
ПРИЛОЖЕНИЕ 2
Таблица 1
ТАБЛИЦА СЛУЧАЙНЫХ ЧИСЕЛ
Таблица 2
ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ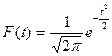 
| 0.0 | 0,3989 | |||||||||
| 0.1 | ||||||||||
| 0.2 | ||||||||||
| 0.3 | ||||||||||
| 0.4 | ||||||||||
| 0.5 | ||||||||||
| 0.6 | ||||||||||
| 0.7 | ||||||||||
| 0.8 | ||||||||||
| 0.9 | ||||||||||
| 1.0 | ||||||||||
| 1.1 | ||||||||||
| 1.2 | ||||||||||
| 1.3 | ||||||||||
| 1.4 | ||||||||||
| 1.5 | ||||||||||
| 1.6 | ||||||||||
| 1.7 | ||||||||||
| 1.8 | ||||||||||
| 1.9 | ||||||||||
| 2.0 | ||||||||||
| 2.1 | ||||||||||
| 2.2 | ||||||||||
| 2.3 | ||||||||||
| 2.4 | ||||||||||
| 2.5 | ||||||||||
| 2.6 | ||||||||||
| 2.7 | ||||||||||
| 2.8 | ||||||||||
| 2.9 | ||||||||||
| 3.0 | ||||||||||
| 4.0 |
Таблица 3
ЗНАЧЕНИЯ χ2 В ЗАВИСИМОСТИ ОТ ЧИСЛА СТЕПЕНЕЙ СВОБОДЫ k И ВЕРОЯТНОСТИ Р
| k | Р | k | Р | ||||
| 0.95 | 0.99 | 0.999 | 0.95 | 0.99 | 0.999 | ||
| 0.00393 | 0.03157 | 0.05157 | 7.962 | 5.812 | 3.942 | ||
| 0.103 | 0.0201 | 0.00200 | 8.672 | 6.408 | 4.416 | ||
| 0.352 | 0.115 | 0.0243 | 9.390 | 7.015 | 4.905 | ||
| 0.711 | 0.297 | 0.0908 | 10.117 | 7.633 | 5.407 | ||
| 1.145 | 0.554 | 0.210 | 10.871 | 8.260 | 5.921 | ||
| 1.635 | 0.872 | 0.381 | 11.591 | 8.897 | 6.447 | ||
| 2.167 | 1.239 | 0.598 | 12.338 | 9.542 | 6.983 | ||
| 2.733 | 1.646 | 0.857 | 13.091 | 10.196 | 7.529 | ||
| 3.325 | 2.088 | 1.152 | 13.848 | 10.856 | 8.035 | ||
| 3.740 | 2.558 | 1.479 | 14.611 | 11.524 | 8.649 | ||
| 4.575 | 3.053 | 1.834 | 15.379 | 12.198 | 9.222 | ||
| 5.226 | 3.571 | 2.214 | 16.151 | 12.879 | 9.803 | ||
| 5.892 | 4.107 | 2.617 | 16.928 | 13.565 | 10.391 | ||
| 6.571 | 4.660 | 3.041 | 17.707 | 14.256 | 10.986 | ||
| 7.261 | 5.229 | 3.483 | 18.493 | 14.953 | 11.588 |