Коэффициент корреляции и его свойства

Из определения ковариации следует, что она имеет размерность, равную произведению размерностей величин X и Y. Другими словами, величина ковариации зависит от единиц измерения случайных величин. По этой причине для одних и тех же двух величин ковариация имеет различные значения в зависимости от того, в каких единицах были измерены величины. Такая особенность ковариации является недостатком этой числовой характеристики, поскольку сравнение ковариаций различных систем случайных величин становится затруднительным. В связи с этим, чтобы устранить указанный недостаток, вводят новую числовую характеристику – коэффициент корреляции:

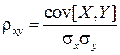. (4.10)

Рассмотрим теперь свойства коэффициента корреляции.

1⁰. Коэффициент корреляции двух независимых случайных величин равен нулю.

Отметим, что обратное утверждение неверно. Например, пусть Y=X² и распределение X симметрично относительно начала координат, т.е. M[X]=0, то M[XY]=M[X³]=0 и M[X]M[Y]=0. Следовательно, K_xy=0 и r_xy=0, несмотря на то, что между X и Y имеется функциональная зависимость.

Таким образом, если коэффициент корреляции между двумя случайными величинами равен нулю, то утверждение, что эти случайные величины независимы – не всегда справедливо. Это значит, что может существовать система зависимых случайных величин, коэффициент корреляции которых равен нулю. Поэтому вводится понятие коррелированности.

Две случайные величины называются коррелированными, если их коэффициент корреляции отличен от нуля; если он равен нулю, то эти величины называются некоррелированными.

Итак, из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин. Заранее отметим, что некоррелированность и независимость совпадают только в одном случае, когда случайные величины подчинены нормальному закону распределения.

2⁰. Коэффициент корреляции r_xy двух случайных величин X и Y не превосходит по абсолютной величине единицы, т.е.

.

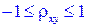3⁰. Коэффициент корреляции двух случайных величин X и Y равен r_xy=±1 тогда и только тогда, когда между величинами X и Y существует линейная функциональная зависимость.

Итак, при возрастании |r_xy| от 0 до 1 корреляционная связь увеличивается, а при |r_xy|=1 она становится линейной функциональной зависимостью. Другими словами, коэффициент корреляции можно рассматривать как меру линейной зависимости между двумя случайными величинами X и Y.

Функция регрессии

Если случайные величины X и Y независимы, то функция распределения двумерной случайной величины {X,Y} равна произведению функций распределения случайных величин, входящих в систему:

F(x,y) = F₁(x)×F₂(y). (4.11)

Выполнение данного равенства является необходимым и достаточным условием независимости двух случайных величин.

В случае ДСВ каждый элемент матрицы распределения равен произведению вероятностей соответствующих величин

p_ij = P(X=x_i)×P(Y=y_j). (4.12)

В случае НСВ плотность распределения равна произведению двух плотностей соответствующих величин

f(x,y) = f₁(x)×f₂(y). (4.13)

Для описания зависимых случайных величин используют т.н. условные распределения, под которыми понимают распределение одно из случайных величин при условии, что другая приняла вполне определенное значение.

Для ДСВ {X,Y}:

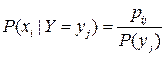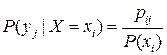, . (4.14)

Условным математическим ожиданием одной из случайных величин, входящих в систему {X,Y}, называется ее математическое ожидание, вычисленное на основе условного распределения:

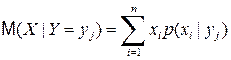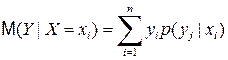, . (4.16)

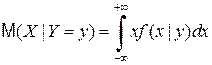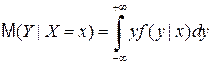, (4.17)

Условное математическое ожидание M[X | y] есть функция от y:

M[X | y] = f(y) (4.18)

и называют регрессией X на Y.

Условное математическое ожидание M[Y | x] есть функция от x:

M[X | y] = f(y) (4.19)

и называют регрессией Y на X.

График функций регрессии называют линиями (кривыми) регрессии. Если случайные величины X и Y независимы, то линии регрессии X на y и Y на x параллельны координатным осям, т.к. математическое ожидание каждой из них не зависят от того, какое значение приняла другая.