Интегрирование сложных дробей
Продолжаем рассматривать интегралы от дробей и корней. Не все они суперсложные, просто по тем или иным причинам примеры были немного «не в тему» в других статьях.
Пример 9
Найти неопределенный интеграл
.
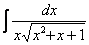В знаменателе под корнем находится квадратный трехчлен плюс за пределами корня «довесок» в виде «икса». Интеграл такого вида решается с помощью стандартной замены.
Решаем:
.
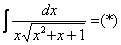Замена тут простая:
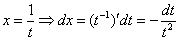
Смотрим на жизнь после замены:
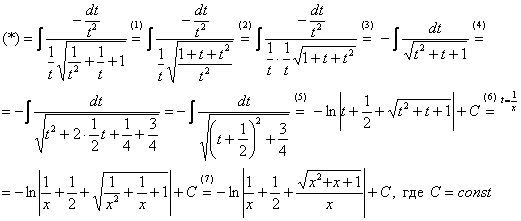
(1) После подстановки приводим к общему знаменателю слагаемые под корнем.
(2) Выносим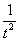 
из-под корня.
(3) Числитель и знаменатель сокращаем на 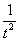. Заодно под корнем мы переставили слагаемые в удобном порядке. При определенном опыте шаги (1), (2) можно пропускать, выполняя прокомментированные действия устно.
(4) Полученный интеграл, как вы помните, решается методом выделения полного квадрата. Выделяем полный квадрат.
(5) Интегрированием получаем заурядный «длинный» логарифм.
(6) Проводим обратную замену. Если изначально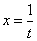 
, то обратно: 
.
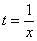(7) Заключительное действие направлено на прическу результата: под корнем снова приводим слагаемые к общему знаменателю и выносим из-под корня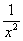 
.
Пример 10
Найти неопределенный интеграл
.
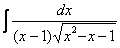Это пример для самостоятельного решения. Здесь к одинокому «иксу» добавлена константа, и замена почти такая же:
.
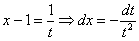Единственное, что нужно, - это дополнительно выразить «икс» из проводимой замены:
.
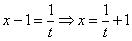Полное решение и ответ в конце урока.
Иногда в таком интеграле под корнем может находиться квадратный двучлен, это не меняет способ решения, оно будет даже еще проще. Почувствуйте разницу:
Пример 11
Найти неопределенный интеграл
.
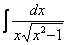Пример 12
Найти неопределенный интеграл
.
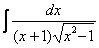Краткие решения и ответы в конце урока. Следует отметить, что Пример 11 является в точности биномиальным интегралом, решение которого рассматривалось на уроке Интегралы от иррациональных функций.
Интеграл от неразложимого в знаменателе многочлена 2-ой степени в степени
Более редкий, но, тем не менее, встречающий в практических примерах вид интеграла.
Пример 13
Найти неопределенный интеграл
.
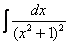В знаменателе подынтегральной функции находится неразложимый на множители квадратный двучлен. Подчеркиваем, что неразложимость на множители является существенной особенностью. Если многочлен раскладывается на множители, то всё намного понятнее, например:
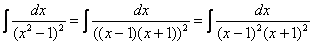– и далее применяется стандартный метод неопределенных коэффициентов.
Вернёмся к примеру со счастливым номером 13. Этот интеграл тоже из разряда тех, с которыми можно изрядно промучиться, если не знаешь, как решать.
Решение начинается с искусственного преобразования:
Как почленно разделить числитель на знаменатель, думаю, уже все понимают.
Полученный интеграл берётся по частям:
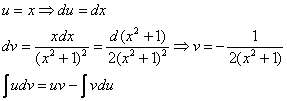
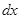
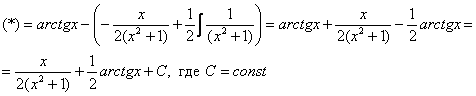
Готово.
Для интеграла вида
,
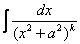где (k ≥ 2) – натуральное число, выведена рекуррентная формула понижения степени:
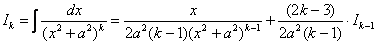, где
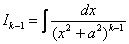; – это интеграл степенью ниже на 1.
Убедимся в справедливости данной формулы для интеграла из Примера 13:
.
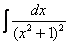В данном случае: k = 2; a2 = 1; используем формулу:
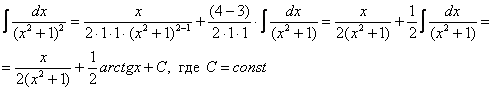
Как видите, ответы совпадают.
Пример 14
Найти неопределенный интеграл
.
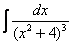Это пример для самостоятельного решения. В образце решения дважды последовательно использована вышеупомянутая формула.
Если под степенью находится неразложимый на множители квадратный трехчлен, то решение сводится к двучлену путем выделения полного квадрата, например:
.
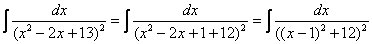Далее следует «безболезненная» линейная замена
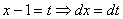и получается знакомый интеграл
.
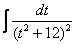Что делать, если дополнительно в числителе есть многочлен? В этом случае используется метод неопределенных коэффициентов, и подынтегральная функция раскладывается в сумму дробей. Если такой интеграл встретится, смотрите учебник – там всё просто.