Глава 5 Затухающие колебания
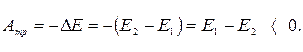 |
В реальных механических колебательных системах при выведении их из положения равновесия кроме квазиупругой силы действует сила трения.
Поскольку она направлена против скорости, работа силы трения отрицательна. Эта работа приводит к уменьшению полной механической энергии колебательной системы.
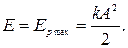 |
Уменьшение энергии колебательной системы приводит к постепенному уменьшению амплитуды колебаний, ибо
В этом случае говорят, что колебания затухают.
Аналогичная ситуация складывается в колебательном контуре. Реальная катушка, входящая в состав контура, всегда обладает активным сопротивлением 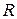 . При протекании тока на активном сопротивлении катушки будет выделяться джоулево тепло
. При протекании тока на активном сопротивлении катушки будет выделяться джоулево тепло 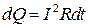 . Энергия контура при этом будет уменьшаться, что будет приводить к уменьшению амплитуды колебаний заряда, напряжения и силы тока.
. Энергия контура при этом будет уменьшаться, что будет приводить к уменьшению амплитуды колебаний заряда, напряжения и силы тока.
Наша задача – выяснить по какому закону происходит уменьшение амплитуды колебаний, по какому закону изменяется сама колеблющаяся величина, с какой частотой происходят затухающие колебания, как долго колебания «затухают».
§1 Затухание колебаний в системах с вязким трением
Рассмотрим колебательную систему, в которой действует сила вязкого трения. Примером такой колебательной системы может служить математический маятник, совершающий колебания в воздушной среде.
В этом случае при выведении системы из положения равновесия на
маятник будут действовать две силы: квазиупругая сила и сила сопротивления (сила вязкого трения).
Второй закон Ньютона запишется следующим образом:
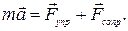 (1)
(1)
Мы знаем, что при малых скоростях сила вязкого трения пропорциональна скорости движения:
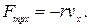 |
Знак «-» указывает на то, что сила вязкого трения всегда направлена против скорости движения тела.
Тогда выражение (1) в проекции на ось ОХ, вдоль которой происходят колебания, будет выглядеть следующим образом:
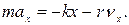 (2)
(2)
 |
Учтем, что проекция скорости есть первая производная от координаты тела, а проекция ускорения – вторая производная от координаты:
Тогда уравнение (2) примет вид:
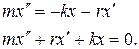 |
Разделив все члены уравнения на m и обозначив
 |
получим уравнение движения в следующем виде:
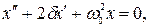 (3)
(3)
где d - коэффициент затухания, он зависит от коэффициента трения r,
w0 - циклическая частота идеальных колебаний (в отсутствие трения).
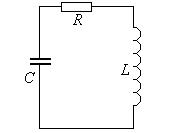 Прежде чем решать уравнение (3), рассмотрим колебательный контур. Активное сопротивление катушки
Прежде чем решать уравнение (3), рассмотрим колебательный контур. Активное сопротивление катушки  включено последовательно с емкостью С и индуктивностью L.
включено последовательно с емкостью С и индуктивностью L.
Запишем второй закон Кирхгофа
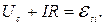
Учтем, что 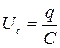 ,
, 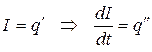 ,
, 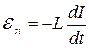 .
.
Тогда второй закон Кирхгофа примет вид:
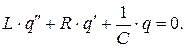
Разделим обе части уравнения на 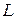 :
:
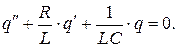
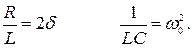 Введем обозначения
Введем обозначения
Окончательно получаем
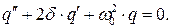 (3')
(3')
Обратите внимание на математическую тождественность дифференциальных уравнений (3) и (3’). В этом нет ничего удивительного. Мы уже показывали абсолютную математическую тождественность процесса колебания маятника и электромагнитных колебаний в контуре. Очевидно, процессы затухания колебаний в контуре и в системах с вязким трением тоже происходят одинаково.
Решив уравнение (3), мы получим ответы на все поставленные выше вопросы.
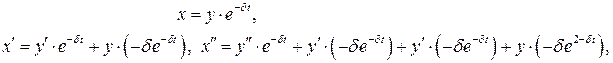 |
Уравнение (3) можно привести к уравнению гармонических колебаний, применив подстановку
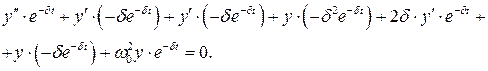 |
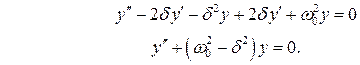 |
Тогда уравнение (3) примет вид
Если d2 < w02, то величина w02 - d2 > 0, ее можно обозначить w2 = w02 - d2 .
Получаем знакомое уравнение гармонических колебаний 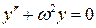 .
.
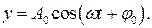 |
Решение этого уравнения нам известно
Тогда для искомого уравнения (3) получаем окончательный результат
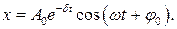 |
Нетрудно видеть, что заряд конденсатора в реальном колебательном контуре будет изменяться по закону
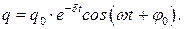
Анализ полученного результата:
1 В результате совместного действия квазиупругой силы и силы сопротивления система может совершать колебательное движение. Для этого должно выполняться условие w02 - d2 > 0. Иными словами, трение в системе должно быть невелико.
2 Частота затухающих колебаний w не совпадает с частотой колебаний системы в отсутствие трения w2 = w02 - d2 < w02. С течение времени частота затухающих колебаний остается неизменной.
Если коэффициент затухания d мал, то частота затухающих колебаний близка к собственной частоте w0 .
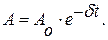 |
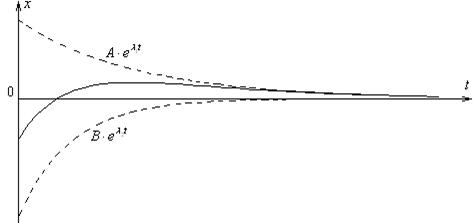
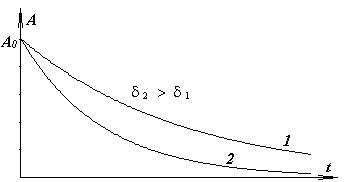
3 Амплитуда затухающих колебаний, как это и было предсказано ранее, уменьшается с течением времени.
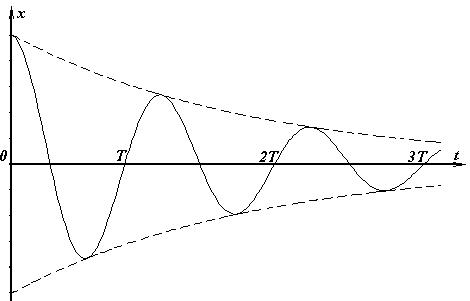 |
Это убывание амплитуды происходит по экспоненциальному закону.
4 Если w02 - d2 < 0, то есть трение в системе велико, то уравнение (3) имеет решение вида
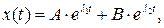 (4)
(4)
где 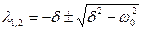 .
.
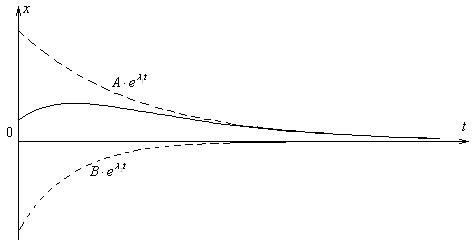 Непосредственной подстановкой легко убедиться, что функция (4) действительно является решением уравнения (3). Очевидно, что сумма двух экспоненциальных функций не является периодической функцией. С физической точки зрения это означает, что колебания в системе не возникнут. После выведения системы из положения равновесия она будет медленно в него возвращаться. Такой процесс называется апериодическим.
Непосредственной подстановкой легко убедиться, что функция (4) действительно является решением уравнения (3). Очевидно, что сумма двух экспоненциальных функций не является периодической функцией. С физической точки зрения это означает, что колебания в системе не возникнут. После выведения системы из положения равновесия она будет медленно в него возвращаться. Такой процесс называется апериодическим.
или
§2 Как быстро затухают колебания в системах с вязким трением?
Декремент затухания
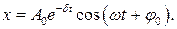 |
Мы показали, что при наличии вязкого трения в системе она совершает колебания, амплитуда которых убывает по экспоненциальному закону:
Быстрота затухания (убывания амплитуды) 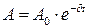 зависит от трения в системе: чем больше коэффициент сопротивления
зависит от трения в системе: чем больше коэффициент сопротивления 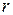 , тем больше
, тем больше
 |
значение величины
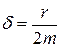 . Видно, что величина d характеризует быстроту затухания колебаний. По этой причине d называют коэффициентом затухания.
. Видно, что величина d характеризует быстроту затухания колебаний. По этой причине d называют коэффициентом затухания. Для электрических колебаний в контуре коэффициент затухания 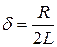 зависит от параметров катушки: чем больше активное сопротивление катушки, тем быстрее убывают амплитуды заряда на конденсаторе, напряжения, силы тока.
зависит от параметров катушки: чем больше активное сопротивление катушки, тем быстрее убывают амплитуды заряда на конденсаторе, напряжения, силы тока.
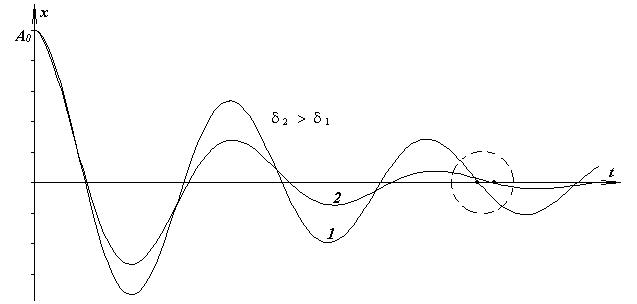 Функция
Функция 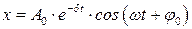 является произведением убывающей показательной функции
является произведением убывающей показательной функции 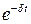 и гармонической функции
и гармонической функции 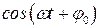 , поэтому функция
, поэтому функция 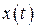 не является гармонической. Но
не является гармонической. Но 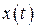 обладает определенной степенью «повторяемости», заключающейся в том, что максимумы, минимумы, нули функции наступают через равные промежутки времени. График функции
обладает определенной степенью «повторяемости», заключающейся в том, что максимумы, минимумы, нули функции наступают через равные промежутки времени. График функции 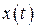 представляет собой синусоиду, ограниченную двумя экспонентами.
представляет собой синусоиду, ограниченную двумя экспонентами.
 |
Найдем отношение двух последовательных амплитуд, разделенных промежутком времени в один период. Это отношение называют декрементом затухания
Обратите внимание, что результат не зависит от того, какие два последовательных периода вы рассматриваете – в начале колебательного движения или по прошествии какого-то времени. За каждый период амплитуда колебаний меняется не на одинаковую величину, а в одинаковое количество раз!!
Нетрудно видеть, что за любые разные промежутки времени амплитуда затухающих колебаний уменьшается в одинаковое количество раз.
Время релаксации
Временем релаксации называется время 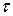 , за которое амплитуда затухающих колебаний уменьшается в е раз:
, за которое амплитуда затухающих колебаний уменьшается в е раз:
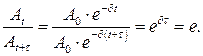
Тогда 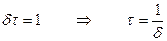 .
.
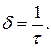 Отсюда нетрудно установить физический смысл коэффициента затухания:
Отсюда нетрудно установить физический смысл коэффициента затухания:
Таким образом, коэффициент затухания 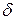 есть величина, обратная времени релаксации
есть величина, обратная времени релаксации 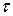 . Пусть, например, в колебательном контуре коэффициент затухания равен
. Пусть, например, в колебательном контуре коэффициент затухания равен 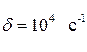 . Это значит, что через время
. Это значит, что через время 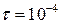 с амплитуда колебаний уменьшится в е раз.
с амплитуда колебаний уменьшится в е раз.
Логарифмический декремент затухания
Часто быстроту затухания колебаний характеризуют логарифмическим декрементом затухания. Для этого берут натуральный логарифм от отношения амплитуд, разделенных промежутком времени в период.
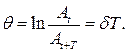 |
Выясним физический смысл логарифмического декремента затухания.
Пусть N – число колебаний, совершаемых системой за время релаксации, то есть число колебаний, за которое амплитуда колебаний уменьшается в е раз. Очевидно, 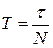 .
.
Тогда
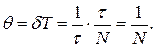
Видно, что логарифмический декремент затухания 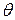 - есть величина, обратная числу колебаний, по прошествии которых амплитуда уменьшается в е раз.
- есть величина, обратная числу колебаний, по прошествии которых амплитуда уменьшается в е раз.
Допустим, 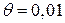 , это значит, что по прошествии 100 колебаний амплитуда уменьшится в е раз.
, это значит, что по прошествии 100 колебаний амплитуда уменьшится в е раз.
Добротность колебательной системы
Кроме логарифмического декремента затухания и времени релаксации, быстроту затухания колебаний можно характеризовать такой величиной, как добротность колебательной системы. Под добротностью
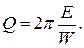 |
понимают увеличенное в 2p раз отношение полной энергии системы Е к энергии W , рассеянной за период:
Очевидно, что чем меньше энергии рассеивается за период за счет работы силы сопротивления, тем больше добротность колебательной системы. В идеальном случае (при отсутствии потерь) добротность колебательной системы стремится к бесконечности.
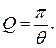 |
Можно показать, что для слабо затухающих колебаний
***
Энергия колебательной системы в произвольный момент времени 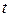 равна
равна 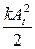 . Потери энергии за период можно найти как разность энергии в момент времени
. Потери энергии за период можно найти как разность энергии в момент времени 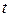 и энергии через время, равное периоду:
и энергии через время, равное периоду:
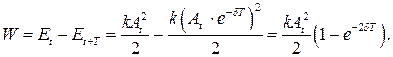
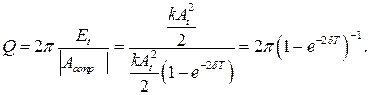 Тогда
Тогда
Показательную функцию можно разложить в ряд 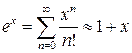 при
при 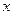 << 1. после подстановки получаем
<< 1. после подстановки получаем 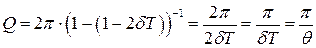 .
.
При выводе нами было наложено ограничение 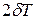 << 1, что верно только для слабо затухающих колебаний. Следовательно, область применения выражения для добротности
<< 1, что верно только для слабо затухающих колебаний. Следовательно, область применения выражения для добротности 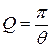 ограничена только слабо затухающими колебаниями. Тогда как выражение
ограничена только слабо затухающими колебаниями. Тогда как выражение 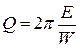 применимо к любой колебательной системе.
применимо к любой колебательной системе.
Формулы, полученные нами для добротности системы, пока ни о чем не говорят. Допустим, расчеты дают значение добротности Q = 10. Что это означает? Как быстро затухают колебания? Это хорошо или плохо?
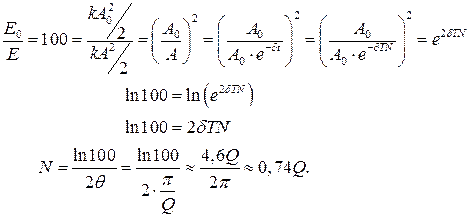 |
Обычно условно считают, что колебания практически прекратились, если их энергия уменьшилась в 100 раз (амплитуда – в 10). Выясним, какое количество колебаний совершила система к этому моменту:
Можем ответить на поставленный ранее вопрос: N = 8.
Какая колебательная система лучше – с большой или малой добротностью? Ответ на этот вопрос зависит от того, что вы хотите получить от колебательной системы.
Если вы желаете, чтобы система совершила как можно больше колебаний до остановки, добротность системы нужно увеличивать. Как? Поскольку добротность определяется параметрами самой колебательной системы, то необходимо правильно эти параметры подобрать.
Например, маятник Фуко, установленный в Исаакиевском соборе, должен был совершать слабо затухающие колебания. Тогда
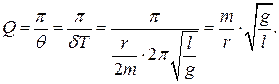
Самый простой способ увеличить добротность маятника – сделать его тяжелее.
В практике нередко возникают и обратные задачи: необходимо по возможности быстрее погасить возникшие колебания (например, колебание стрелки измерительного прибора, колебания кузова автомобиля, колебания судна и т.д.) приспособления, позволяющие увеличить затухание в системе, называются демпферами (или амортизаторами). Например, амортизатор автомобиля в первом приближении представляет собой цилиндр, заполненный маслом (вязкой жидкостью), в котором может двигаться поршень, имеющий ряд мелких отверстий. Шток поршня соединен с кузовом, а цилиндр – с осью колеса. Возникшие колебания кузова быстро затухают, так как движущийся поршень встречает на своем пути большое сопротивление со стороны вязкой жидкости, заполняющей цилиндр.
§3 Затухание колебаний в системах с сухим трением
Принципиально иначе происходит затухание колебаний, если в системе действует сила трения скольжения. Именно она является причиной остановки пружинного маятника, совершающего колебания вдоль какой-либо поверхности.
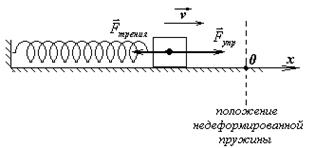 |
Допустим, пружинный маятник, расположенный на горизонтальной поверхности, привели в колебательное движение, сжав пружину и отпустив груз, то есть из крайнего положения. В процессе движения груза из одного крайнего положения в другое на него действуют сила тяжести и сила реакции опоры (по вертикали), сила упругости и сила трения скольжения (вдоль поверхности).
Заметим, что в процессе движения слева направо сила трения неизменна по направлению и модулю.
Этот позволяет утверждать, что в течение первой половины периода пружинный маятник находится в постоянном силовом поле.
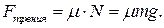 |
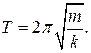 |
В постоянном силовом поле у пружинного маятника изменяется лишь положение равновесия, оно смещается влево, период же остается неизменным
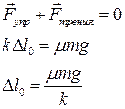 |
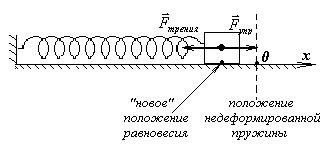
Смещение положения равновесия можно рассчитать из условия равенства равнодействующей нулю в положении равновесия:
 |
Важно, что в течение первой половины периода колебания маятника гармонические!
При движении в обратном направлении – справа налево- сила трения изменит направление, но в течение всего перехода будет оставаться постоянной по модулю и направлению. Эта ситуация опять таки соответствует колебаниям маятника в постоянном силовом поле. Только теперь это поле другое! Оно изменило направление. Следовательно, положение равновесия при движении справа налево тоже изменилось. Теперь оно сместилось вправо на величину Dl0.
Изобразим зависимость координаты тела от времени. Поскольку за каждую половину периода движение представляет собой гармоническое колебание, то график будет представлять собой половинки синусоид, каждая из которых построена относительно своего положения равновесия. Мы будем производить операцию «сшивания решений».
Покажем, как это делается на конкретном примере.
Пусть масса груза, прикрепленного к пружине, равна 200 г, жесткость пружины 20 Н/м, коэффициент трения между грузом и поверхностью стола 0,1. Маятник привели в колебательное движение, растянув пружину на
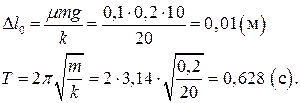 |
6,5 см.
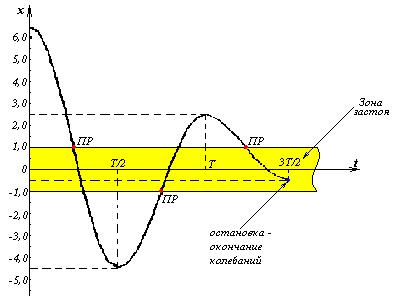
В отличие от колебательных систем с вязким трением в системах с сухим трением амплитуда колебаний убывает с течением времени по линейному закону – за каждый период она уменьшается на две ширины зоны застоя.
Другая отличительная особенность - колебания в системах с сухим трением даже теоретически не могут происходить бесконечно долго. Они прекращаются, как только тело останавливается в «зоне застоя».
§4 Примеры решения задач
Задача 1 Характер изменения амплитуды затухающих колебаний в системах с вязким трением
Амплитуда затухающих колебаний маятника за время t1 = 5 мин уменьшилась в 2 раза. За какое время t2 амплитуда колебаний уменьшится в 8 раз? Через какое время t3 можно считать, что колебания маятника прекратились?
Решение:
Амплитуда колебаний в системах с вязким трением с течением време-
ни уменьшается по экспоненте 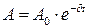 , где
, где 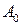 - амплитуда колебаний в начальный момент времени,
- амплитуда колебаний в начальный момент времени, 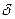 - коэффициент затухания.
- коэффициент затухания.
1 Запишем закон изменения амплитуда два раза
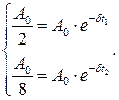
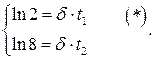 2 Решаем уравнения совместно. Логарифмируем каждое уравнение и получаем
2 Решаем уравнения совместно. Логарифмируем каждое уравнение и получаем
Делим второе уравнение не первое и находим время t2
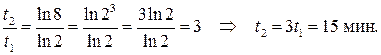
3 Колебания можно считать прекратившимися, когда энергия системы уменьшится в 100 раз:
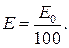
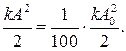 4 Энергия системы равна максимальной потенциальной энергии маятника
4 Энергия системы равна максимальной потенциальной энергии маятника
После преобразований получаем
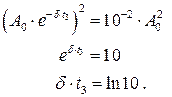
Делим последнее уравнение на уравнение (*)
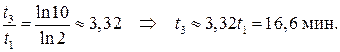
Задача 2 Период затухающих колебаний в системах с вязким трением
Определите период затухающих колебаний системы Т, если период собственных колебаний Т0 = 1 с, а логарифмический декремент затухания 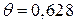 . Сколько колебаний совершит эта система до полной остановки?
. Сколько колебаний совершит эта система до полной остановки?
Решение:
1 Период затухающих колебаний в системе с вязким трением больше периода собственных колебаний ( при отсутствии трения в системе). Частота затухающих колебаний, наоборот, меньше частоты собственных и равна 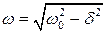 , где
, где 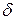 - коэффициент затухания.
- коэффициент затухания.
2 Выразим циклическую частоту через период . 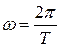 и учтем, что логарифмический декремент затухания равен
и учтем, что логарифмический декремент затухания равен 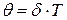 :
:
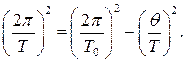
3 После преобразований получаем 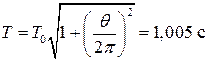 .
.
4 Колебания можно считать прекратившимися, когда энергия системы уменьшится в 100 раз:
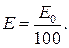
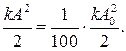 Энергия системы равна максимальной потенциальной энергии маятника
Энергия системы равна максимальной потенциальной энергии маятника
После преобразований получаем
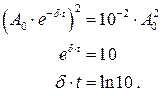
5 Выражаем коэффициент затухания через логарифмический декремент 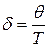 , получаем
, получаем 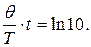
Число колебаний, которое совершит система до остановки, равно 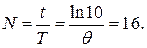
Задача 3 Число колебаний, совершаемых маятником до уменьшения амплитуды в два раза
Логарифмический декремент затухания маятника равен q = 3×10-3. Определите число полных колебаний, которое должен совершить маятник, чтобы амплитуда его колебаний уменьшилась в 2 раза.
Решение:
1 Амплитуда колебаний в системах с вязким трением с течением времени уменьшается по экспоненте 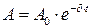 , где
, где 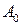 - амплитуда колебаний в начальный момент времени,
- амплитуда колебаний в начальный момент времени, 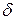 - коэффициент затухания.
- коэффициент затухания.
Поскольку амплитуда колебаний уменьшается в 2 раза, получаем
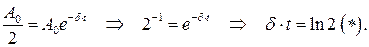
2 Время колебаний 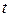 можно представить как произведение периода колебаний
можно представить как произведение периода колебаний 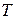 на их количество
на их количество 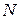 :
:
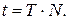
Подставляем полученное значение времени в выражение (*)
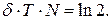
3 Нетрудно видеть, что 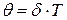 - логарифмический декремент затухания. Получаем
- логарифмический декремент затухания. Получаем 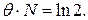
Находим число колебаний 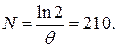
Задача 4 Добротность колебательной системы
Определите добротность маятника, если за время, в течение которого было совершено 10 колебаний, амплитуда уменьшилась в 2 раза. Через какое время маятник остановится?
Решение:
1 Амплитуда колебаний в системах с вязким трением с течением времени уменьшается по экспоненте 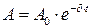 , где
, где 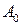 - амплитуда колебаний в начальный момент времени,
- амплитуда колебаний в начальный момент времени, 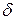 - коэффициент затухания.
- коэффициент затухания.
Поскольку амплитуда колебаний уменьшается в 2 раза, получаем
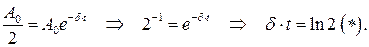
2 Время колебаний 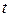 можно представить как произведение периода колебаний
можно представить как произведение периода колебаний 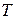 на их количество
на их количество 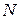 :
:
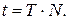
Подставляем полученное значение времени в выражение (*)
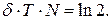
3 Нетрудно видеть, что 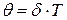 - логарифмический декремент затухания. Получаем
- логарифмический декремент затухания. Получаем 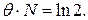 Логарифмический декремент затухания равен
Логарифмический декремент затухания равен
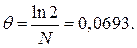
4 Добротность колебательной системы 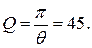
5 Колебания можно считать прекратившимися, когда энергия системы уменьшится в 100 раз:
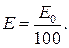
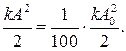 Энергия системы равна максимальной потенциальной энергии маятника
Энергия системы равна максимальной потенциальной энергии маятника
После преобразований получаем
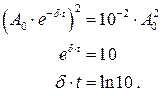
 Находим время, через которое колебания прекратятся
Находим время, через которое колебания прекратятся 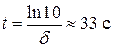 .
.
Задача 5 Колебания магнита
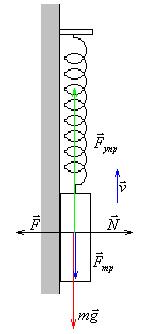 Вася Лисичкин, известный на всю школу экспериментатор, решил заставить колебаться магнитную фигурку любимого литературного героя Колобка по стенке холодильника. Он прикрепил фигурку к пружине жесткостью k = 10 H/м, растянул ее на 10 см и отпустил. Сколько колебаний совершит Колобок, если масса фигурки m = 10 г, коэффициент трения между фигуркой и стенкой равен μ = 0,4 , а оторвать ее от стенки можно силой F = 0,5 Н.
Вася Лисичкин, известный на всю школу экспериментатор, решил заставить колебаться магнитную фигурку любимого литературного героя Колобка по стенке холодильника. Он прикрепил фигурку к пружине жесткостью k = 10 H/м, растянул ее на 10 см и отпустил. Сколько колебаний совершит Колобок, если масса фигурки m = 10 г, коэффициент трения между фигуркой и стенкой равен μ = 0,4 , а оторвать ее от стенки можно силой F = 0,5 Н.
Решение:
1 При движении из крайнего нижнего в крайнее верхнее положение, когда скорость груза направлена вверх, сила трения скольжения направлена вниз и численно равна 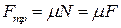 . Таким образом, пружинный маятник находится в постоянном силовом поле, созданном силами тяжести и трения. В постоянном силовом поле у маятника смещается положения равновесия:
. Таким образом, пружинный маятник находится в постоянном силовом поле, созданном силами тяжести и трения. В постоянном силовом поле у маятника смещается положения равновесия:
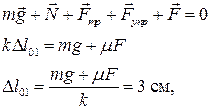
где 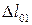 - растяжение пружины в новом «положении равновесия».
- растяжение пружины в новом «положении равновесия».
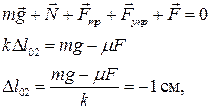
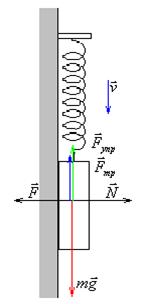 2 При движении из крайнего верхнего в крайнее нижнее положение, когда скорость груза направлена вниз, сила трения скольжения направлена вверх и численно равна
2 При движении из крайнего верхнего в крайнее нижнее положение, когда скорость груза направлена вниз, сила трения скольжения направлена вверх и численно равна 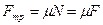 . Таким образом, пружинный маятник опять-таки находится в постоянном силовом поле, созданном силами тяжести и трения. В постоянном силовом поле у маятника смещается положения равновесия:
. Таким образом, пружинный маятник опять-таки находится в постоянном силовом поле, созданном силами тяжести и трения. В постоянном силовом поле у маятника смещается положения равновесия:
где 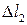 - деформация пружины в новом «положении равновесия», знак «-» говорит, что в этом положении пружина сжата.
- деформация пружины в новом «положении равновесия», знак «-» говорит, что в этом положении пружина сжата.
3 Зона застоя ограничена деформациями пружины от - 1 см до 3 см и составляет 4 см. Середина зоны застоя, в которой деформация пружины равна 1 см, соответствует положению груза, в котором сила трения отсутствует. В зоне застоя сила упругости пружины по модулю меньше равнодействующей максимальной силы трения покоя и силы тяжести. Если маятник останавливается в зоне застоя, колебания прекращаются.
4 За каждый период деформация пружины уменьшается на две ширины зоны застоя, т.е. на 8 см. После одного колебания деформация пружины станет равной 10 см – 8 см = 2 см. Это означает, что после одного колебания фигурка Колобка попадает в зону застоя и ее колебания прекращаются.
§5 Задания для самостоятельного решения
Тест «Затухающие колебания»
1 Под затуханием колебаний понимают…
А) уменьшение частоты колебаний; Б) уменьшение периода колебаний;
В) уменьшение амплитуды колебаний; Г) уменьшение фазы колебаний.
2 Причина затухания свободных колебаний –
А) действие на систему случайных факторов, тормозящих колебания;
Б) действие периодически изменяющейся внешней силы;
В) наличие в системе силы трения;
Г) постепенное уменьшение квазиупругой силы, стремящейся вернуть маятник в положение равновесия.
3 Из приведенных ниже уравнений движения выберите то, которое соответствует затухающим колебаниям в системе с вязким трением.
А) 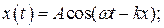 Б)
Б) 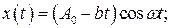
В) 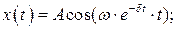 Г)
Г) 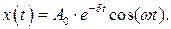
4 Два одинаковых математических маятника колеблются, один в вакууме, другой в сжатом воздухе . Сравните период колебания Т маятника в воздухе с периодом колебания маятника в вакууме 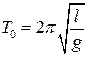 .
.
А) Т > 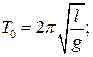 Б) Т <
Б) Т < 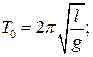 В) Т =
В) Т = 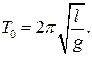
5 Математический маятник начал колебаться с амплитудой 9 см. Через некоторое время 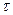 амплитуда колебаний стала равной 6 см. Какой будет амплитуда колебаний через следующий промежуток времени
амплитуда колебаний стала равной 6 см. Какой будет амплитуда колебаний через следующий промежуток времени 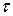 ?
?
А) 5 см ; Б) 4 см ; В) 3 см;
Г) Ответ дать не возможно, поскольку неизвестно время 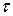 .
.
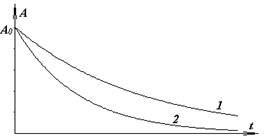 6 Два одинаковых маятника, находясь в разных вязких средах, совершают колебания. Амплитуда этих колебаний меняется с течением времени так, как показано на рисунке. В какой среде трение больше?
6 Два одинаковых маятника, находясь в разных вязких средах, совершают колебания. Амплитуда этих колебаний меняется с течением времени так, как показано на рисунке. В какой среде трение больше?
А) 1; Б) 2;
В) Ответ дать невозможно, поскольку по осям координат не проставлен масштаб и выполнить расчеты нельзя.
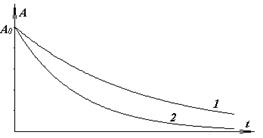 7 Два маятника, находясь в одинаковых средах, совершают колебания. Амплитуда этих колебаний меняется с течением времени так, как показано на рисунке. Какой маятник имеет большую массу?
7 Два маятника, находясь в одинаковых средах, совершают колебания. Амплитуда этих колебаний меняется с течением времени так, как показано на рисунке. Какой маятник имеет большую массу?
А) 1; Б) 2;
В) Ответ дать невозможно, поскольку по осям координат не проставлен масштаб и выполнить расчеты нельзя.
8 На каком рисунке правильно показана зависимость координаты затухающих колебаний в системе с вязким трением от времени?
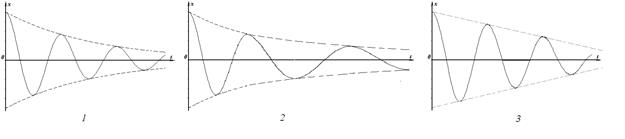
А) 1; Б) 2; В) 3; Г) Все графики верные.
9 Установите соответствие между физическими величинами, характеризующими затухание колебаний в системах с вязким трением, и их определением и физическим смыслом. Заполните таблицу
| Физическая величина | Определение, физический смысл | расчетная формула |
| Время релаксации | ||
| Декремент затухания | ||
| Логарифмический декремент затухания |
А) Это отношение амплитуд колебаний через время, равное периоду;
Б) Это натуральный логарифм отношения амплитуд колебаний через время, равное периоду;
В) Это время, в течение которого амплитуда колебаний уменьшается в е раз;
Г) 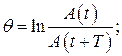 Д)
Д) 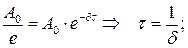 Е)
Е) 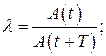
Ж) Эта величина обратна числу колебаний, за которое амплитуда колебаний уменьшается в е раз;
З) Эта величина показывает во сколько раз уменьшается амплитуда колебаний за время, равное периоду колебаний.
10 Составьте правильное утверждение.
Под добротностью понимают…
А) увеличенное в 2p раз отношение полной энергии системы E к энергии W , рассеянной за период;
Б) отношение амплитуд через промежуток времени, равный периоду;
В) количество колебаний, которое совершает система к тому моменту, когда амплитуда уменьшится в е раз.
Добротность рассчитывают по формуле…
А) 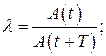 Б)
Б) 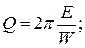 В)
В) 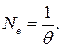
Добротность колебательной системы зависит от…
А) энергии системы;
Б) потерь энергии за период;
В) параметров колебательной системы и трения в ней.
Чем больше добротность колебательной системы, тем …
А) медленнее затухают колебания;
Б) быстрее затухают колебания.
11 Математический маятник приводят в колебательное движение, отклонив подвес от положения равновесия в первом случае на 15°, во втором – на 10°. В каком случае маятник совершит больше колебаний до остановки?
А) Когда подвес отклонили на 15°;
Б) Когда подвес отклонили на 10°;
В) В обоих случаях маятник совершит одинаковое число колебаний.
12 К двум нитям одинаковой длины прикрепили шарики одинакового радиуса – алюминиевый и медный. Маятники приводят в колебательное движение, отклонив их на одинаковые углы. Какой из маятников совершит большее количество колебаний до остановки?
А) Алюминиевый; Б) Медный;
В) Оба маятника совершат одинаковое количество колебаний.
13 Пружинный маятник, расположенный на горизонтальной поверхности, привели в колебания, растянув пружину на 9 см. После совершения трех полных колебаний маятник оказался на расстоянии 6 см от положения недеформированной пружины. На каком расстоянии от положения недеформированной пружины окажется маятник после следующих трех колебаний?
А) 5 см; Б) 4 см; В) 3 см.
