Способы задания графов

Глава II. Теория графов.

(Лекция 3)

История теории графов

Родоначальником теории графов является Леонард Эйлер (1707 – 1782).

В 1736 году Эйлер решил задачу о Кенигсбергских мостах. Задача состояла в следующем:

«Найти маршрут прохождения всех четырех систем (см. рис.), который бы начинался в любом из них, кончался на этой же части и ровно один раз проходил по каждому из них.»

Река «Треголь» Þ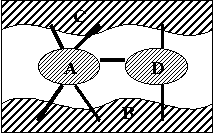

Эйлер доказал невозможность такого маршрута. Он обозначил части суши точками, а мосты – линиями, и получил Граф (мультиграф):

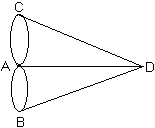
Утверждение о существовании положительного решения задачи о Кенигсбергских мостах эквивалентно утверждению о невозможности обойти этот граф.

Эйлер нашел критерий существования обхода у графа: Граф должен быть связанным и каждая его вершина должна быть инцидентна четному числу ребер.

После этого более ста лет теория графов не развивалась.

В 1847 году Кирхгофф, рассматривая электрические цепи, каждую из них заменял на соответствующий граф.

В 1857 году Келли открыл важный класс графа – деревья. Он стремился перечислить число изомерных предельных углеводородов.

С_nH_2n+2

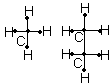
В 1869 Жордан независимо от Келли ввел и изучал деревья, как отдельные математические объекты.

Основные понятия Теории графов

Для описания строения различных систем, состоящих из взаимосвязанных элементов, часто используют графические схемы, изображая сами эти элементы точками, а связи между ними – линиями, соединяющими эти точки.

(Лекция 4)

При этом получаются диаграммы:

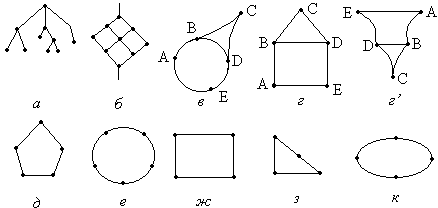
На этих диаграммах ни располож6ение точек на рисунке, ни форма и длина линий не играют никакой роли. Существенно лишь, какие именно пары соединены линиями. Эти диаграммы означают модель связи структурных элементов. Таким образом, диаграммы в, г и г’ обозначают одну и ту же структуру связи элементов A, B, C, D, E. На них обозначены связи между элементами: (A, B), (B, C), (C, D), (D, E), (E, A), (D, B). Порядок элементов в этих парах не важен, поэтому они называются неупорядоченными. Пары элементов, а также рисунки в, г и г’ обозначают одни и тот же математический объект.

Определение. Графом G называется пара множеств V и E (G = (V, E)), где V не пустое множество, а Е – некоторое множество неупорядоченных пар элементов множества V (E = {(V_i, V_j)}, i = 1, 2, 3, …, n, j = 1, 2, 3, …, n, i ¹ j, где n – число вершин графа).

Определение. Элементы множества V называются вершинами, а элементы Е – ребрами.

Пример: На диаграмме в: V = {A, B, C, D, E}, E = {(A, B), (B, C), (C, D), (D, E), (E, A), (D, B)}.

Определение. Две вершины, соединяемые ребром, называются смежными, и каждая из этих вершин называется инцидентной данному ребру.

Определение. Если два различных ребра х и у инцедентны одной и той же вершине, то они называются смежными.

Определение. Число вершин, смежных с данной вершиной U, называются степенью этой вершины. Если степень вершины равна нулю, то такая вершина называется изолированной.

Определение. Граф называется конечным, если множество его вершин конечно, то есть множество V конечно.

Определение. Граф с p вершинами и q ребрами называется (p, q) граф.

Пример: (1, 0) – тривиальный граф.

Определение. Граф G’ = (V’, E’) называется подграфом графа G, если V’ Í V, E’ Í E.

Примеры:

G: 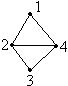V = {1, 2, 3, 4};

G’: 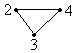V’ = {2, 3, 4}, V’ Í E Þ G’ – подграф графа G.

G’’: 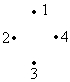V’’ = V, E’’ = Æ Ì E Þ G’’ – подграф графа G.

Геометрическая интерпретация графа (диаграмма)

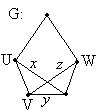
Смежные вершины: U и V, U и W.

Инцидентность: U инцидентно ребру x, V инцидентно ребру y, V инцидентно ребру z, W инцидентно ребру z.

Смежные ребра: x и y, y и z.

Степень: degV = 3.

Виды графов

Существуют различные виды графов:

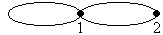
Определение. Если в графе существуют несколько ребер, соединяющих одну и ту же пру вершин, то такие ребра называются кратными.

Определение. Если в графе существуют ребра, соединяющие одну и ту же вершину, то такие ребра называются петлями.

Определение. Если в графе существуют кратные ребра, то такой граф называется мультиграфом. Если в графе существуют еще и петли, то такой граф называется псевдографом.

Будем рассматривать конечные неориентированные графы без петель.

Определение. Граф называется неориентированным, если все его ребра – это неупорядоченные пары его вершин.

Определение. Последовательность ребер p = {(V₀, V₁), (V₁, V₂), …, (V_n-1, V_n)} называется путем, соединяющим V₀ и V_n. Длиной пути называется число ребер в такой плоскости.

Пример:

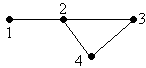(1, 2), (2, 3), (3, 4) – путь, соединяющий вершины 1 и 4. Его длина равна 3.

Определение. Путь называется простым, если все вершины графа, по которым он проходит, различны (более одного раза не проходит по одной вершине).

Определение. Путь называется замкнутым, если он начинается и заканчивается на одной вершине (V₀ = V_n).

Определение. Циклом называется замкнутый путь, не проходящий более одного раза по тому и тому же ребру.

Пример:

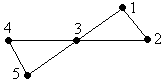
Циклы: 1) (1, 2), (2, 3), (3, 1).

2) (5, 4), (4, 3), (3, 5).

3) (1, 3), (3, 4), (4, 5), (5, 3), (3, 2), (2, 1).

(1-й и 3-й циклы различаются только длиной пути)

Определение. Цикл называется простым, если он более одного раза не проходит через одну и ту же вершину, то есть V₀, …, V_n-1 – различные.

Определение. Граф называется связанным, если для любых двух вершин в нем существует путь, соиденяющий эти вершины.

Примеры:

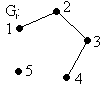Граф G₁ не связанный, так как 5 – изолированная вершина.

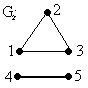Граф G₂ не связанный, так как не существует путей, соединяющих (3, 4).

Свойства путей и циклов:

1) Если в графе имеется путь, соиденяющий вершины А и В, то в нем имеется простой путь, соединяющий эти вершины.

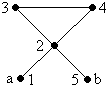Путь: (1, 2, 3, 4, 2, 5). Простой путь: (1, 2, 5).

Доказательство: Пусть существует p = {(V₀, V₁), (V₁, V₂), …, (V_n-1, V_n)}, который соединяет вершины А (V₀), В (V_n). Вообще говоря этот путь не обязан быть простым Þ p = {(V₀, V₁), (V₁, V₂), …, (V_i-1, V_i), …,(V_j-1, V_j), …, (V_n-1, V_n)}.Если V_i = V_j (i ¹ j), то p - непростой путь. Если участок V_i … V_j выбросить, то образуется новая последовательность V, которая будет путем, так как V_i = V_j, причем этот путь будет простым, поскольку он будет как минимум дважды не проходит по одному ребру.

2) Если в графе имеется цикл, проходящий через ребро(А, В), в этом графе имеется и простой цикл, проходящий через ребро (А, В).

Доказательство: Путь p - не простой путь. Сделаем его простым (по доказательству первого свойства). После этого мы получим путь p₁ – простой, p₁ = {(V₀, V₁), (V₁, V₂), …, (V_n-1, V_n)}, где V₀ = А, V_n = В. Сделаем из него цикл, дописав ребро (V_n, V₀). Таким образом получился цикл, являющийся простым, поскольку он построен по простому пути.

3) Если в графе степень каждой вершины не меньше 2, то в этом графе имеется цикл.

Доказательство: Возьмем самый длинный простой пути, который имеется в этом графе: p = {(V₀, V₁), (V₁, V₂), …, (V_n-1, V_n)}. Есть еще какая-то вершина W, с которой соединяется V_n (по условию). Или W = V_i (i = 1, 2, …, n-1) или W = V_j (j > n). Рассмотрим второй случай, тогда получится противоречие с тем, что мы выбрали самый длинный простой путь. Значит W = V_i (i = 1, 2, …, n-1). Таким образом мы получили цикл.

(Лекция 5)

Способы задания графов

1) Задание списка вершин и ребер. G = (V, E)

2) Геометрическая интерпретация (графический способ).

3) Матричный.

А) Матрица смежности

Определение. Граф называется помеченным (перенумерованным), если его вершины отличаются одна от другой какими-либо методами.

Пример:

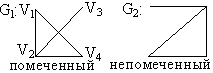
Определение. Матрицей смежности конечного графа G (A(G) = ||V_ij|| (i, j = 1, 2, …, p)) с p вершинами называется матрица размером p ´ p, в которой:

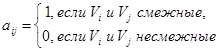
Пример:

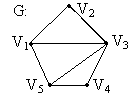
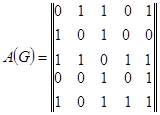
Заметим, что deg V_i равна числу единиц в i-ой строке или i-ом столбце.

б) Матрица инцидентности

Обозначается: I(G) = (b_ij), i = 1,2, …, p, j = 1, 2, …, q, где p – число вершин, q – число ребер.

Определение. Матрицей инцидентностиграфа G с p вершинами и q ребрами называется p ´ p матрица, в которой: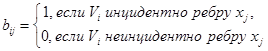

Пример:

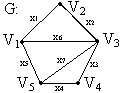
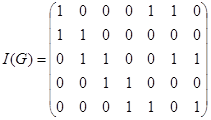
Заметим, что:

1) Каждый столбец матрицы I(G) содержит ровно две единицы и никакие две строки не идентичны.

(в каждом столбце содержится ровно две единицы, так как каждое ребро соединяет только две вершины; никакие две строки не идентичны по причине отсутствия кратных ребер).

2) Число единиц в i-ой строке равно степени вершины V_i.

3) Матрица инцидентности полезна при решении задач теории графов, касающихся циклов.

4) Матрица инцидентности требует больший объем памяти по сравнению с матрицей смежности.