Предел функции в точке. Свойства предела

По Гейне:

Число А называется пределом функции f(x) в точке x₀, если для любой последовательность значений аргумента ({x_n}→x₀) соответствующая последовательность значений функции f(x) стремится к числу А.

По Коши:

Число А называется пределом функции f(x) в точке x₀ если для любого e>0, найдется такое число d>0, что при всех x из условия 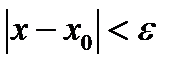будет выполняться неравенство 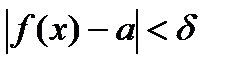(значение функции попадает в d окрестность точки А)

Свойства пределов.

1)Если функция имеет предел, то только один.

2) lim C=C, где С – постоянная величина

3) предел произведения равен произведению пределов

4) константы можно выносить за знак предела

5)

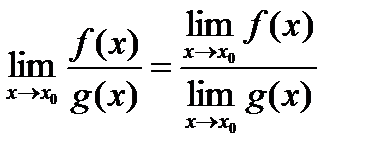
Предел функции на бесконечности. Бесконечно большие и бесконечно малые функции, их свойства.

Предел функции на бесконечности в математическом анализе описывает поведение значения данной функции, когда её аргумент становится бесконечно большим по модулю.

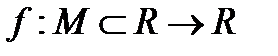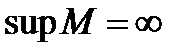Пусть задана числовая функция с неограниченной сверху областью определения, то есть и Число 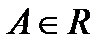называется пределом функции f при x стремящемся к бесконечности, если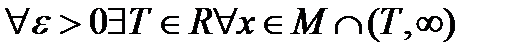

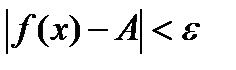
Пишут: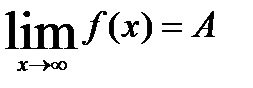

Бесконечно большие функции.

Ранее мы рассмотрели случаи, когда функция f(x) стремилась к некоторому конечному пределу b при x → a или x → ∞.

Рассмотрим теперь случай, когда функция y=f(x) стремится к бесконечности при некотором способе изменения аргумента.

Функция f(x) стремится к бесконечности при x → a, т.е. является бесконечно большой величиной, если для любого числа М, как бы велико оно ни было, можно найти такое δ > 0, что для всех значений х≠a, удовлетворяющих условию |x-a| < δ, имеет место неравенство |f(x)| > M.

Если f(x) стремится к бесконечности при x→a, то пишут 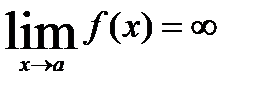или f(x)→∞ при x→a.

Если f(x) стремится к бесконечности при x→a и при этом принимает только положительные или только отрицательные значения, соответственно пишут 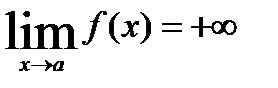или .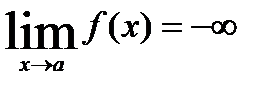

Бесконечно малые функции.

Функция y=f(x) называется бесконечно малой при x→a или при x→∞, ес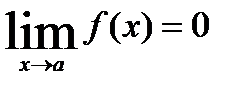ли или 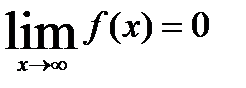, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Свойства.

1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.

3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.

Соотношение между бесконечно большими и бесконечно малыми функциями.

Теорема Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a. Две функции называются эквивалентными, если 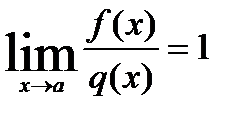. Если 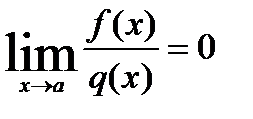, то бесконечно малая f(x) есть функция большего порядка малости.