Методика изучения внетабличного умножения и деления в начальной школе
Ведущие принципы обучения математике в младших классах – органическое сочетание обучения и воспитания, усвоение знаний и развитие познавательных способностей детей, практическая направленность обучения, выработка необходимых для этого навыков. Большое значение в связи со спецификой математического материала придаётся учёту возрастных и индивидуальных особенностей восприятия его детьми.
Внетабличное умножение однозначных чисел и соответствующие случаи деления рассматриваются в теме «Числа от 1 до 100», которая изучается на третьем году обучения. Всего на тему «Внетабличное умножение и деление» отводится 28 часов.
Уверенное овладение детьми навыками устных и письменных вычислений является одной из основных задач начального обучения математике, так как это необходимо для продолжения обучения.
Случаи умножения однозначного числа на однозначное являются табличными. Таким образом, к внетабличным случаям относится умножение двузначного числа на однозначное. Прием устного умножения должен основываться на знании учащимися таблицы умножения. Поэтому двузначные множители необходимо привести к такому виду, который допускал бы использование таблицы умножения. Для этого двузначные множители представляются в виде суммы разрядных слагаемых (одно из слагаемых – однозначное число, второе – круглые десятки). При сложении и вычитании круглых десятков использовался прием замены круглых десятков однозначными именованными числами. Таким же образом, умножение и деление круглых десятков на однозначное число может быть сведено к умножению однозначного именованного числа на однозначное: 40 · 2 = 4 дес. · 2 = 8 дес., т.е. 40 · 2 = 80. Умножение двузначного числа на однозначное выполняется так:
24 · 3 = (20 + 4) · 3 = 20 · 3 + 4 · 3 = 60 + 12 = 72
Операцию разложения числа на разрядные слагаемые учащиеся выполняют устно. К этому времени они умеют устно находить произведение однозначных чисел, сумму двузначных чисел. Поэтому для того чтобы сформировать у учащихся умение устно умножить двузначные числа на однозначные, необходимо ознакомить их еще с двумя операциями: умножением суммы на число и умножением круглых десятков на однозначное число. Методика изучения последней операции, как было показано выше, весьма проста, поэтому остановимся подробно на методике обучения умножению суммы на число.
Методика изучения этой темы (как и изучение всех математических понятий в начальной школе) основывается на использовании системы целесообразных задач, наглядных интерпретациях их содержания. Чтобы выяснить их особенности, воспользуемся определением умножения через сумму для случая, когда один из множителей представлен суммой:
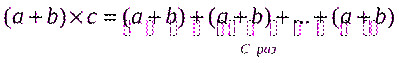
Правую часть этого равенства графически можно представить в виде с рядов объектов одного рода, причем в каждом ряду содержится a объектов одного вида и b объектов другого. В качестве таких объектов можно взять кружки двух видов – светлые и темные (рис. 1).
















 ……. …….
……. …….
……. ……..
………………… ………………… c







 ………………… …………………
………………… …………………

 ……. ………
……. ………
а b
Рис. 1
В соответствии с таким рисунком легко составить содержательные задачи, являющиеся средством формирования правила умножения суммы на число. Например: «В отряде 4 звена. В каждом звене 5 девочек и 4 мальчика. Сколько всего человек в отряде?», «На субботнике по благоустройству школьного двора каждому отряду было поручено посадить по 2 клена и по 3 липы. Сколько всего деревьев должны были посадить 5 отрядов?» и т. д.
Для каждой из таких задач составляются выражения двух видов (в соответствии с двумя возможными способами их решения), которые также можно проиллюстрировать графически:
(5 + 4)·4 5·4 + 4·4
(2 + 3)·5 2·5 + 3·5 и т. д.
Соответствие двух разных выражений одной и той же конкретной ситуации делает факт равенства этих выражений очевидным.
Затем учащимся предлагается самостоятельно составить содержательные задачи по выражениям вида (a+b)·cи а · с + b·с.
Прием умножения суммы на число отрабатывается на числовых выражениях. Упражнения подбираются так, чтобы ученики могли выбрать наиболее удобный способ вычислений. Например, значение выражения (2 + 4) · 6 удобнее вычислять как произведение (умножение 6·6 — табличное). Значение выражения (9 + 5) · 8 определяется в три действия: 9·8 + 5·8, поскольку умножать 14 на 8 учащиеся еще не умеют.
