Глава 4 Свободные электрические колебания

Под электрическими колебаниями понимают периодические изменения заряда, силы тока и напряжения. Простейшая система, в которой возможны свободные электрические колебания, - это так называемый колебательный контур. Это устройство, состоящее из соединенных между собой конденсатора и катушки. Будем полагать, что активное сопротивление катушки отсутствует, в этом случае контур называют идеальным. При сообщении этой системе энергии в ней будут происходить незатухающие гармонические колебания заряда на конденсаторе, напряжения и тока.

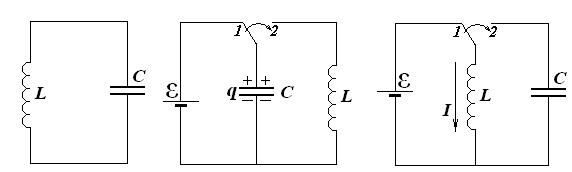
Сообщить колебательному контуру энергию можно разными способами. Например, зарядив конденсатор от источника постоянного тока или возбудив ток в катушке индуктивности. В первом случае энергией обладает электрическое поле между обкладками конденсатора. Во втором, энергия заключена в магнитном поле тока, текущего по цепи.

§1 Уравнение колебаний в контуре

Докажем, что при сообщении контуру энергии в нем будут происходить незатухающие гармонические колебания. Для этого необходимо получить дифференциальное уравнение гармонических колебаний вида .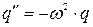

Допустим, конденсатор зарядили и замкнули на катушку. Конденсатор начнет разряжаться, по катушке потечет ток. Согласно второму закону Кирхгофа сумма падений напряжений вдоль замкнутого контура равна сумме ЭДС в этом контуре .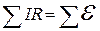

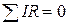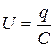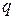В нашем случае падение напряжения поскольку контур идеальный. Конденсатор в цепи ведет себя как источник тока, в качестве ЭДС выступает разность потенциалов между обкладками конденсатора , где - заряд на конденсаторе, 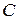- электроемкость конденсатора. Кроме того, при протекании через катушку изменяющегося тока в ней возникает ЭДС самоиндукции 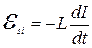, где 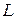- индуктивность катушки, 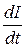- скорость изменения тока в катушке. Поскольку ЭДС самоиндукции препятствует процессу разрядки конденсатора второй закон Кирхгофа принимает вид

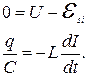
Но ток в контуре – это ток разрядки или зарядки конденсатора, следовательно 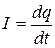. Тогда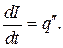

Дифференциальное уравнение преобразуется к виду

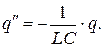
Введя обозначение 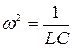, получим известное нам дифференциальное уравнение гармонических колебаний .

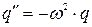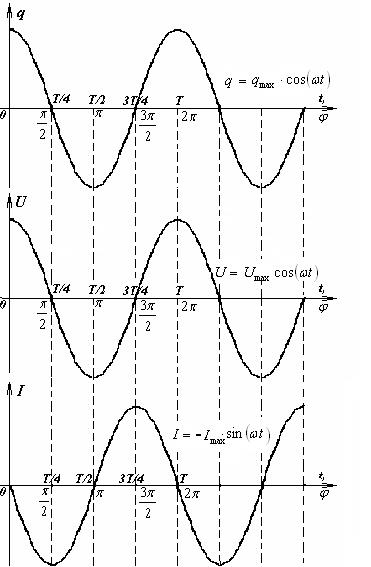
Это означает, что заряд на конденсаторе в колебательном контуре будет изменяться по гармоническому закону

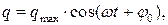
где 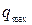- максимальное значение заряда на конденсаторе, 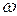- циклическая частота, 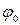- начальная фаза колебаний.

Период колебаний заряда 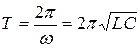. Это выражение носит название формулы Томпсона.

Напряжение на конденсаторе

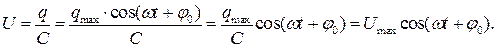
Ток в цепи

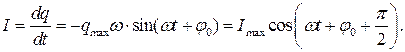
Видим, что кроме заряда на конденсаторе по гармоническому закону будут изменять еще ток в контуре и напряжение на конденсаторе. Напряжение колеблется в одной фазе с зарядом, а сила тока опережает заряд по

фазе на .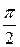

Энергия электрического поля конденсатора

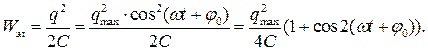
Энергия магнитного поля тока

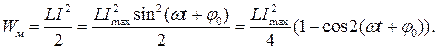
Таким образом, энергии электрического и магнитного полей тоже изменяются по гармоническому закону, но с удвоенной частотой.

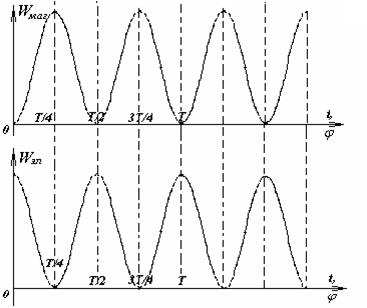
Подведем итог

Под электрическими колебаниями следует понимать периодические изменения заряда, напряжения, силы тока, энергии электрического поля, энергии магнитного поля. Эти колебания, как и механические, могут быть как свободными, так и вынужденными, гармоническим и негармоническим. Свободные гармонические электрические колебания возможны в идеальном колебательном контуре.

§2 Процессы, происходящие в колебательном контуре

Мы математически доказали факт существования свободных гармонических колебаний в колебательном контуре. Однако, остается неясным, почему такой процесс возможен. Что является причиной возникновения колебаний в контуре?

В случае свободных механических колебаний такая причина была найдена – это внутренняя сила, возникающая при выведении системы из по- ложения равновесия. Эта сила в любой момент направлена к положению равновесия и пропорциональна координате тела (со знаком «минус»). Попробуем найти аналогичную причину возникновения колебаний в колебательном контуре.

Пусть колебания в контуре возбуждают, зарядив конденсатор и замкнув его на катушку.

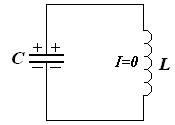В начальный момент времени заряд на конденсаторе максимален. Следовательно, напряжение и энергия электрического поля конденсатора тоже максимальны.

Ток в контуре отсутствует, энергия магнитного поля тока равна нулю.

Первая четверть периода – разрядка конденсатора.

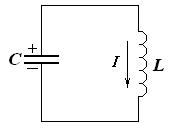Обкладки конденсатора, имеющие разные потенциалы, соединили проводником, поэтому конденсатор начинает разряжаться через катушку. Заряд, напряжение на конденсаторе и энергия электрического поля убывают.

Ток, появившийся в цепи, нарастает, однако, его нарастанию препятствует ЭДС самоиндукции, возникающая в катушке. Энергия магнитного поля тока увеличивается.

Прошла четверть периода - конденсатор разрядился.

Конденсатор разрядился, напряжение на нем стало равным нулю. Энергия электрического поля в этот момент тоже равна нулю. По закону сохранения энергии исчезнуть она не могла. Энергия поля конденсатора полностью перешла в энергию магнитного поля катушки, которая в этот момент достигает своего максимального значения. Максимален ток в цепи.

Казалось бы, в этот момент ток в цепи должен прекратиться, ибо исчезла причина возникновения тока – электрическое поле. Однако, исчезновению тока опять таки препятствует ЭДС самоиндукции в катушке. Теперь она будет поддерживать убывающий ток, и он будет продолжать течь в прежнем направлении, заряжая конденсатор. Начинается вторая четверть периода.

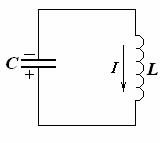Вторая четверть периода – перезарядка конденсатора.

Ток, поддерживаемый ЭДС самоиндукции, продолжает течь в прежнем направлении, постепенно уменьшаясь. Этот ток заряжает конденсатор в противоположной полярности. Заряд и напряжение на конденсаторе увеличиваются.

Энергия магнитного поля тока, убывая, переходит в энергию электрического поля конденсатора.

Прошла вторая четверть периода – конденсатор перезарядился.

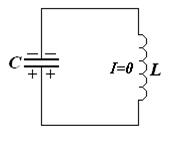Конденсатор перезаряжается до тех пор, пока существует ток. Поэтому в тот момент, когда ток прекращается, заряд и напряжение на конденсаторе принимают максимальное значение.

Энергия магнитного поля в этот момент полностью перешла в энергию электрического поля конденсатора.

Ситуация в контуре в этот момент, эквивалентна исходной. Процессы в контуре повторятся, но в обратном направлении. Одно полное колебание в контуре, длящееся в течение периода, закончится, когда система вернется в исходное состояние, то есть когда конденсатор перезарядится в первоначальной полярности.

Нетрудно видеть, что причиной возникновения колебаний в контуре служит явление самоиндукции. ЭДС самоиндукции препятствует изменению тока: она не дает ему мгновенно нарастать и мгновенно исчезать.

Кстати, будет не лишним сопоставить выражения для расчета квазиупругой силы в механической колебательной системе и ЭДС самоиндукции в контуре:

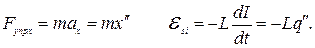
Ранее были получены дифференциальные уравнения для механической и электрической колебательной систем:

Несмотря на принципиальные отличия физических процессов к механических и электрических колебательных системах, явно просматривается математическая тождественность уравнений, описывающих процессы в этих системах. Об этом следует поговорить подробнее.

§3 Аналогия между электрическими и механическими колебаниями

Внимательный анализ дифференциальных уравнений для пружинного маятника и колебательного контура, а так же формул, связывающих величины, характеризующих процессы в этих системах, позволяет выявить, какие величины ведут себя одинаково (таблица 2).

Пружинный маятник	Колебательный контур
Координата тела 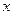( 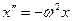)	Заряд на конденсаторе ( )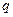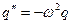
Скорость тела	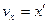Сила тока в контуре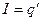
Потенциальная энергия упруго деформированной пружины	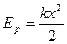Энергия электрического поля конденсатора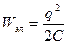
Кинетическая энергия груза	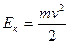Энергия магнитного поля катушки с током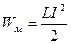
Величина, обратная жесткости пружины	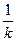Емкость конденсатора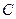
Масса груза	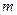Индуктивность катушки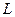
Сила упругости	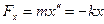ЭДС самоиндукции, равная напряжению на конденсаторе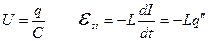

Таблица 2

Важно не просто формальное сходство между величинами, описывающими процессы колебания маятника и процессы в контуре. Тождественны сами процессы!

Крайние положения маятника эквивалентны состоянию контура, когда заряд на конденсаторе максимален.

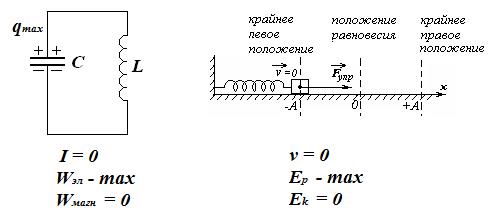
Положение равновесия маятника эквивалентно состоянию контура, когда конденсатор разряжен. В этот момент сила упругости обращается в ноль, а в контуре отсутствует напряжение на конденсаторе. Скорость маятника и сила тока в контуре максимальны. Потенциальная энергия упругой деформации пружины и энергия электрического поля конденсатора равны нулю. Энергия системы состоит из кинетической энергии груза или из энергии магнитного поля тока.

Разрядка конденсатора протекает аналогично движению маятника из крайнего положения в положение равновесия. Процесс перезарядки конденсатора тождественен процессу удаления груза из положения равновесия в крайнее положение.

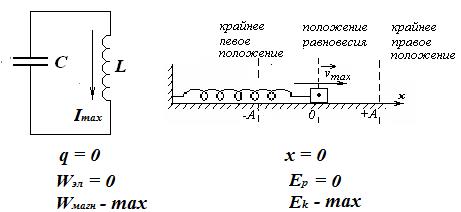
Полная энергия колебательной системы 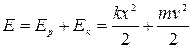или 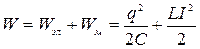остается неизменной с течением времени.

Подобная аналогия может быть прослежена не только между пружинным маятником и колебательным контуром. Всеобщи закономерности свободных колебаний любой природы! Эти закономерности, проиллюстрированные на примере двух колебательных систем (пружинном маятнике и колебательном контуре) не просто можно, а нужно видеть в колебаниях любой системы.

В принципе, можно решить задачу о любом колебательном процессе, заменив его колебаниями мятника. Для этого достаточно грамотно построить эквивалентную механическую систему, решить механическую задачу и провести замену величин в окончательном результате. Например, нужно найти период колебаний в контуре, содержащем конденсатор и две катушки, соединенные параллельно.

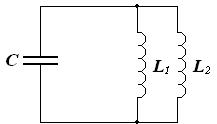Колебательный контур содержит один конденсатор и две катушки. Поскольку катушка ведет себя как груз пружинного маятника, а конденсатор как пружина, то эквивалентная механическая система должна содержать одну пружину и два груза. Вся проблема в том, как грузы прикреплены к пружине. Возможны два случая: один конец пружины закреплен, а к свободному концу прикреплен один груз, второй находится на первом или грузы прикреплены к разным концам пружины.

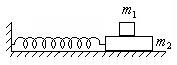
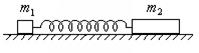
При параллельном соединении катушек разной индуктивности токи по ним текут разные. Следовательно, скорости грузов в тождественной механической системе тоже должны быть разными. Очевидно, это возможно лишь во втором случае.

Период этой колебательной системы нами уже найден. Он равен 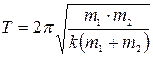. Заменяя массы грузов на индуктивности катушек, а величину, обратную жесткости пружины, на емкость конденсатора, получаем .

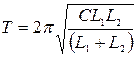§4 Колебательный контур с источником постоянного тока

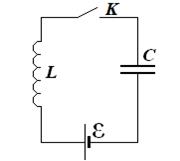Рассмотрим колебательный контур, содержащий источник постоянного тока. Пусть конденсатор первоначально не заряжен. Что будет происходить в системе после замыкания ключа К? Будут ли в этом случае наблюдаться колебания и какова их частота и амплитуда?

Очевидно, после замыкания ключа конденсатор начнет заряжаться. Записываем второй закон Кирхгофа:

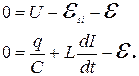
Ток в контуре – это ток зарядки конденсатора, следовательно 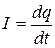. Тогда 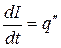. Дифференциальное уравнение преобразуется к виду

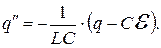
*Решаем уравнение заменой переменных.

Обозначим 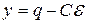. Дифференцируем дважды и с учетом того, что 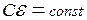, получаем 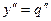. Дифференциальное уравнение приобретает вид

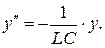
Это дифференциальное уравнение гармонических колебаний, его решением является функция

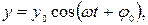
где 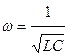- циклическая частота, константы интегрирования 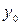и 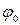находятся из начальных условий.

Заряд на конденсаторе меняется по закону

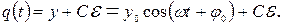
Сразу после замыкания ключа заряд на конденсаторе равен нулю 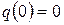и ток в контуре отсутствует 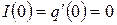. С учетом начальных условий получаем систему уравнений:

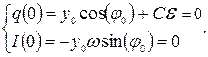
Решая систему, получаем 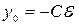и 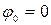. После замыкания ключа заряд на конденсаторе изменяется по закону .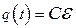

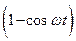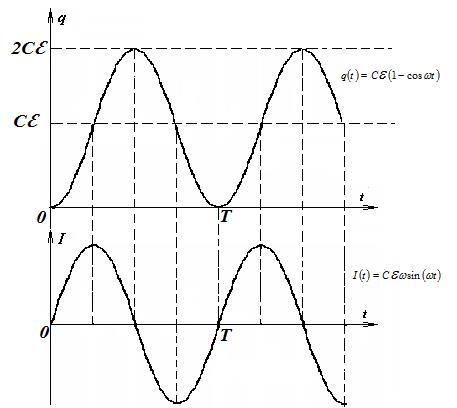
Нетрудно видеть, что в контуре происходят гармонические колебания. Наличие в контуре источника постоянного тока не повлияло на частоту колебаний, она осталась равной 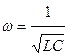. Изменилось «положение равновесия» - в тот момент, когда ток в цепи максимален, конденсатор заряжен. Амплитуда колебаний заряда на конденсаторе равна Cε.

Этот же результат можно получить проще, используя аналогию между колебаниями в контуре и колебаниями пружинного маятника. Источник постоянного тока эквивалентен постоянному силовому полю, в которое помещен пружинный маятник, например, полю тяготения. Отсутствие заряда на конденсаторе в момент замыкания цепи тождественно отсутствию деформации пружины в момент приведения маятника в колебательное движение.

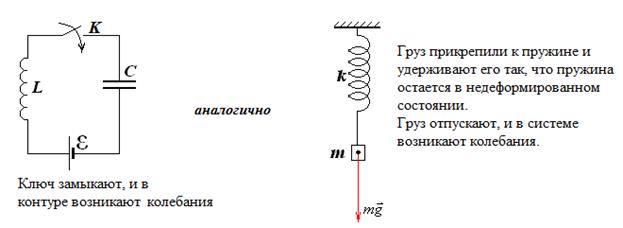В постоянном силовом поле период колебаний пружинного маятника не изменяется. Период колебаний в контуре ведет себя так же – он остается неизменным при введении в контур источника постоянного тока .

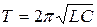В положении равновесия, когда скорость груза максимальна, пружина деформирована:

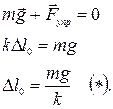
Когда ток в колебательном контуре максимален 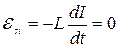. Второй закон Кирхгофа запишется следующим образом

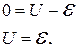
В этот момент заряд на конденсаторе равен 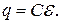Этот же результат можно было получить на основании выражения (*), выполнив замену

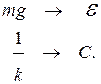
§5 Примеры решения задач

Задача 1Закон сохранения энергии

В колебательном контуре, состоящем из катушки индуктивностью L = 0,5 мкГн и конденсатора емкостью С = 20 пФ происходят электрические колебания. Чему равно максимальное напряжение на конденсаторе, если амплитуда тока в контуре 1 мА? Активное сопротивление катушки пренебрежимо мало.

Решение:

1 Поскольку активным сопротивлением катушки можно пренебречь, полная энергия системы, состоящая из энергии электрического поля конденсатора и энергии магнитного поля катушки, остается неизменной с течением времени:

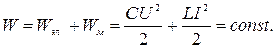(1)

2 В тот момент, когда напряжение на конденсаторе максимально (максимален заряд на конденсаторе), ток в цепи отсутствует. Полная энергия системы состоит только из энергии электрического поля конденсатора

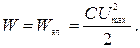(2)

3 В момент, когда ток в цепи максимален, конденсатор полностью разряжен. Полная энергия системы состоит только из энергии магнитного поля катушки

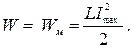(3)

4 На основании выражений (1), (2), (3) получаем равенство 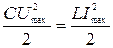. Максимальное напряжение на конденсаторе равно

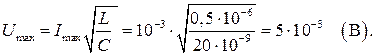
Задача 2Закон сохранения энергии

В колебательном контуре, состоящем из катушки индуктивностью L и конденсатора емкостью С , происходят электрические колебания с периодом Т = 1 мкс. Максимальное значение заряда 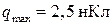. Чему равен ток в контуре в тот момент, когда заряд на конденсаторе равен 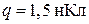? Активное сопротивление катушки пренебрежимо мало.

Решение:

1 Поскольку активным сопротивлением катушки можно пренебречь, полная энергия системы, состоящая из энергии электрического поля конденсатора и энергии магнитного поля катушки, остается неизменной с течением времени:

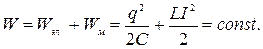(1)

2 В тот момент, когда заряд на конденсаторе максимален, ток в цепи отсутствует. Полная энергия системы состоит только из энергии электрического поля конденсатора

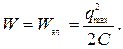(2)

3 На основании (1) и (2) получаем равенство 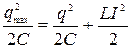. Ток в контуре равен .

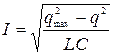4 Период колебаний в контуре определяется формулой Томсона 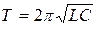. Отсюда 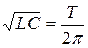. Тогда для тока в контуре получаем

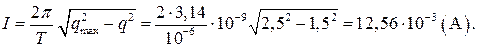
Задача 3Колебательный контур с двумя параллельно соединенными конденсаторами

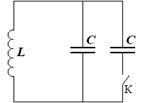В колебательном контуре, состоящем из катушки индуктивностью L и конденсатора емкостью С, происходят электрические колебания с амплитудой заряда 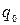. В тот момент, когда заряд на конденсаторе максимален , замыкают ключ К. Каким станет период колебаний в контуре после замыкания ключа? Чему равна амплитуда тока в контуре после замыкания ключ? Омическим сопротивлением контура пренебречь.

Решение:

1 Замыкание ключа приводит к появлению в контуре еще одного конденсатора, подключенного параллельно первому. Общая емкость двух параллельно соединенных конденсаторов равна .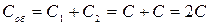

Период колебаний в контуре зависит только от его параметров и не зависит от того, как в системе возбудили колебания и какую энергию сооб- щили системе для этого. Согласно формуле Томсона .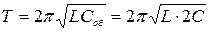

2 Для нахождения амплитуды тока выясним, какие процессы происходят в контуре после замыкания ключа.

Второй конденсатор подключили в тот момент, когда заряд на первом конденсаторе был максимален, следовательно, ток в контуре отсутствовал.

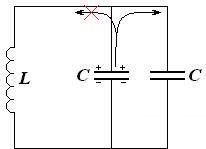
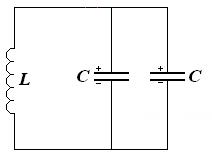Контурный конденсатор должен начать разряжаться. Ток разрядки, дойдя до узла, должен бы разделиться на две части. Однако, в ветви с катушкой, возникает ЭДС самоиндукции, препятствующая нарастанию тока разрядки. По этой причине весь ток разрядки потечет в ветвь с конденсатором, омическое сопротивление которой равно нулю. Ток прекратится, как только сравняются напряжения на конденсаторах, при этом первоначальный заряд конденсатора 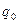перераспределится между двумя конденсаторами. Время перераспределения заряда между двумя конденсаторами ничтожно мало вследствие отсутствия омического сопротивления в ветвях с конденсаторами. За это время ток в ветви с катушкой возникнуть не успеет. Колебания в новой системе продолжатся уже после перераспределения заряда между конденсаторами.

Важно понять, что в процессе перераспределения заряда между двумя конденсаторами энергия системы не сохраняется! До замыкания ключа энергией обладал один конденсатор, контурный:

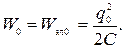
После перераспределения заряда энергией обладает батарея конденсаторов:

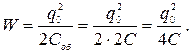
Нетрудно видеть, что энергия системы уменьшилась!

3 Новую амплитуду тока найдем, воспользовавшись законом сохранения энергии. В процессе колебаний энергия батареи конденсаторов переходит в энергию магнитного поля тока:

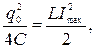
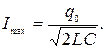
Обратите внимание, закон сохранения энергии начинает «работать» только после завершения перераспределения заряда между конденсаторами.

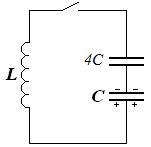Задача 4 Колебательный контур с двумя последовательно соединенными конденсаторами

Колебательный контур состоит из катушки индуктивностью L и двух последовательно соединенных конденсаторов С и 4С. Конденсатор емкостью С заряжен до напряжения 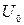, конденсатор емкостью 4С не заряжен. После замыкания ключа в контуре начинаются колебания. Чему равен период этих колебаний? Определите амплитуду тока, максимальное и минимальное значения напряжения на каждом конденсаторе.

Решение:

1 В момент, когда ток в цепи максимален, ЭДС самоиндукции в катушке отсутствует 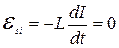. Записываем для этого момента второй закон Кирхгофа

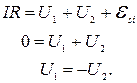
Видим, что в тот момент, когда ток в контуре максимален, конденсаторы заряжены до одинакового напряжения, но в противоположной полярности:

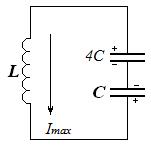
2 До замыкания ключа полная энергия системы состояла только из энергии электрического поля конденсатора С:

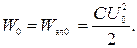
В момент, когда ток в цепи максимален, энергия системы складывается из энергии магнитного поля тока и энергии двух заряженных до одинакового напряжения конденсаторов:

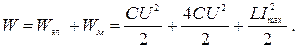
Согласно закону сохранения энергии

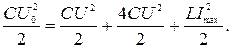
Для нахождения напряжения на конденсаторах воспользуемся законом сохранения заряда – заряд нижней обкладки конденсатора С частично перешел на верхнюю обкладку конденсатора 4С:

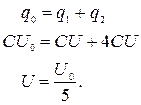
Подставляем найденное значение напряжения в закон сохранения энергии и находим амплитуду тока в контуре:

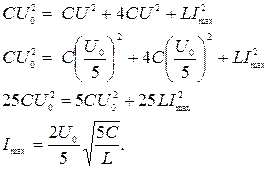
3 Найдем, в каких пределах изменяется напряжение на конденсаторах в процессе колебаний.

Понятно, что в момент замыкания цепи на конденсаторе С было максимальное напряжение 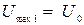. Конденсатор 4С был не заряжен, следовательно, .

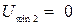После замыкания ключа конденсатор С начинает разряжаться, а конденсатор емкостью 4С – заряжаться. Процесс разрядки первого и зарядки второго конденсаторов заканчивается, как только прекращается ток в цепи. Это произойдет через половину периода. Согласно законам сохранения энергии и электрического заряда:

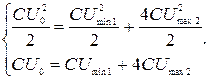
Решая систему, находим:

.

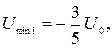
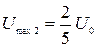Знак «минус» означает, что через полпериода конденсатор емкости С заряжен в полярности, обратной первоначальной.

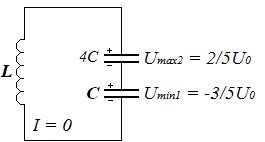
Задача 5Колебательный контур с двумя последовательно соединенным катушками

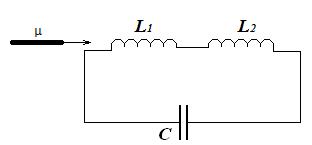Колебательный контур состоит из конденсатора емкостью С и двух катушек индуктивностью L₁ и L₂ . В тот момент, когда ток в контуре принял максимальное значение 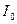, в первую катушку быстро (по сравнению с периодом колебаний) вносят железный сердечник, что приводи к увеличению ее индуктивности в μ раз. Чему равна амплитуда напряжения в процессе дальнейших колебаний в контуре?

Решение:

1 При быстром внесении сердечника в катушку должен сохраниться магнитный поток (явление электромагнитной индукции). Поэтому быстрое изменение индуктивности одной из катушек приведет к быстрому изменению тока в контуре.

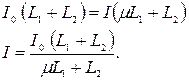
2 За время внесения сердечника в катушку заряд на конденсаторе измениться не успел, он остался незаряженным (сердечник вносили в тот момент, когда ток в цепи был максимален). Через четверть периода энергия магнитного поля тока перейдет в энергию заряженного конденсатора:

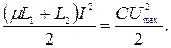
Подставляем в полученное выражение значение тока I и находим амплитуду напряжения на конденсаторе:

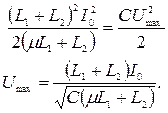
Задача 6Колебательный контур с двумя параллельно соединенным катушками

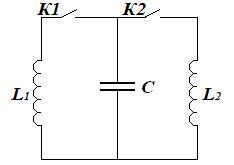Катушки индуктивности L₁ и L₂ подключены через ключи К1 и К2 к конденсатору емкостью С. В начальный момент оба ключа разомкнуты, а конденсатор заряжен до разности потенциалов 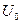. Сначала замыкают ключ К1 и, когда напряжение на конденсаторе станет равным нулю, замыкают К2. Определите максимальное напряжение на конденсаторе после замыкания К2. Сопротивлениями катушек пренебречь.

Решение:

1 При разомкнутом ключе К2 в контуре, состоящем из конденсатора и первой катушки, происходят колебания. К моменту замыкания К2 энергия конденсатора перешла в энергию магнитного поля тока в первой катушке :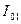

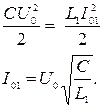
2 После замыкания К2 в колебательном контуре оказываются две катушки, соединенные параллельно.

Ток в первой катушке не может прекратиться вследствие явления самоиндукции. В узле он делится: одна часть тока идет во вторую катушку, а другая заряжает конденсатор .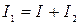

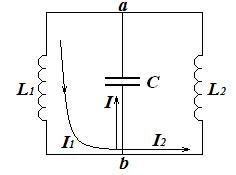
3 Напряжение на конденсаторе станет максимальным, когда прекратится ток I, заряжающий конденсатор. Очевидно, что в этот момент токи в катушках сравняются .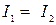

4 На основании закона сохранения энергии

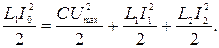
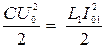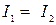С учетом того, что и , получаем

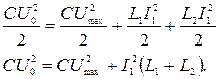
5 Для нахождения тока 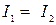запишем для ветвей, содержащих катушки, закон Ома для неоднородного участка цепи:

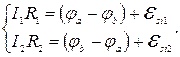
Складываем уравнения с учетом того, что омическим сопротивлением катушек можно пренебречь:

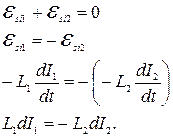
Интегрируем с учетом то, что ток в первой катушке меняется от 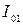до 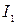, ток во второй катушке изменяется от нуля до :

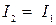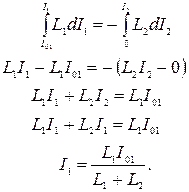
6 Подставляя значение тока 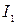в закон сохранения энергии, находим максимальное напряжение на конденсаторе:

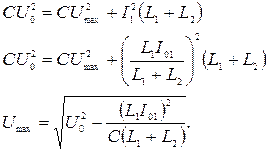
После подстановки значения 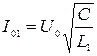получаем:

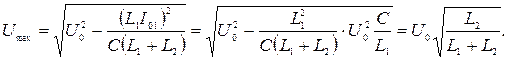
7 Можно было решить задачу, используя механическую аналогию. Колебательный контур состоит из двух катушек и конденсатора, следовательно, эквивалентная механическая система должна состоять из одной пружины и двух грузов.

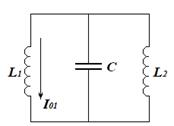
Колебательный контур	Механическая аналогия
Катушки соединены параллельно, следовательно, на них одинаковое напряжение	На грузы действуют одинаковые по модулю силы – оба груза прикреплены к пружине
Сразу после замыкания К2 в первой катушке существовал ток	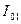В начальный момент первый груз имел скорость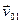
Сразу после замыкания К2 ток во второй катушке отсутствовал	В начальный момент второй груз покоился
Каково максимальное значения напряжения на конденсаторе?	Чему равна максимальная сила упругости, возникающая в пружине в процессе колебаний?

Маятник двигается поступательно со скоростью центра масс 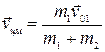и совершает колебания относительно центра масс.

Сила упругости максимальна в момент максимальной деформации пружины. Очевидно, в этот момент относительная скорость грузов становится равной нулю, а относительно стола грузы двигаются со скоростью центра масс. Записываем закон сохранения энергии:

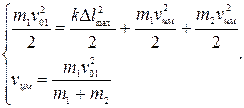
Решая систему, находим

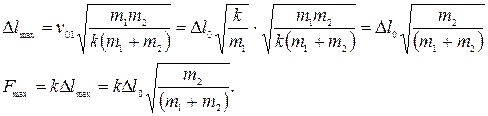
Производим замену

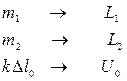
и получаем для максимального напряжения найденное ранее значение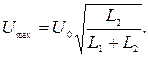

§6 Задания для самостоятельного решения

Упражнение1 Расчет периода и частоты собственных колебаний

1 В колебательный контур входят катушка переменной индуктивности, изменяющаяся в пределах L₁ = 0,5 мкГн до L₂ = 10 мкГн, и конденсатор, емкость которого может изменяться в пределах от С₁ = 10 пФ до

С₂ =500 пФ. Какой диапазон частот можно охватить настройкой этого контура?

2 Во сколько раз изменится частота собственных колебаний в контуре, если его индуктивность увеличить в 10 раз, а емкость уменьшить в 2,5 раза?

3 Колебательный контур с конденсатором емкость 1 мкФ настроен на частоту 400 Гц. Если подключить к нему параллельно второй конденсатор, то частота колебаний в контуре становится равной 200 Гц. Определите емкость второго конденсатора.

4 Колебательный контур состоит из катушки и конденсатора. Во сколько раз изменится частота собственных колебаний в контуре, если в контур последовательно включить второй конденсатор, емкость которого в 3 раза меньше емкости первого?

5 Определите период колебаний контура, в состав которого входит катушка (без сердечника) длины в = 50 см м площади поперечного сечения

S = 3 cм², имеющая N = 1000 витков, и конденсатора емкости С = 0,5 мкФ.

6 В состав колебательного контура входит катушка индуктивности L = 1,0 мкГн и воздушный конденсатор, площади пластин которого S = 100 cм². Контур настроен на частоту 30 МГц. Определите расстояние между пластинами. Активное сопротивление контура пренебрежимо мало.