Определители и их свойства

Определитель – детерминант квадратной и только квадратной матрицей называется некоторая величина, которая получается из ее элементов с помощью следующих правил и соглашений.

I. Договоримся считать определением матрицы размерами 1*1 ее единственный элемент

II. Будем называть дополнительным минором к элементу 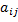матрицы А определитель матрицы, который получается из данной вычеркиванием(стиранием) элемента 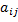вместе со строчкой и столбцом. Обозначают его обычно буквой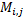

И тут же определим так называемое алгебраическое дополнение к элементу 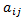обозначив его как величину

Определителем детерминанта квадратной и только квадратной матрицы называется некая величина которая получается из ее элементов с помощью следующих правил.

В частности для определителя квадратной матрицы размерами 2 2 читается определитель квадратной матрицы.

Основные свойства определителя:

Следствие: Определитель матрицы можно считать разложение по любому столбику

При умножении строки(столбца) матрицы на число ее определитель при этом умножится на это число. Следствие: Общий множитель строки/столбца модно выносить за знак определителя.

Определитель матрицы не меняется, если к любой ее строчки прибавить другую параллельную строчку. Даже умноженную на любое число

Если в определитель матрицы поменять местами любые две строчки то он сменит знак. Если определитель имеет две пропорциональные строчки то он равен нулю

7. Обратная матрица и правило её нахождения.

Как известно взаимообратными числами называется такая пара произведения которые равны единицы. Оказывается что и среди матриц есть такие (!) которая обладает главным свойством числовой единицы, это квадратные матрицы у которых

Будем называть две матрицы взаимообратными если их произведение равно, единичной матрицы. Обозначать их принято одной и той же буквой, над одной из ник ставится индекс символ “ ”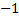

То есть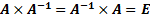

Алгоритм нахождения обратной матрицы:

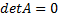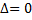Если , то 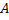обратной не имеет

Если же 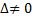, то составляет так называемую присоединенную матрицу 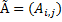которая состоит из соответствующих алгебраических дополнений (элементов) матрицы A.

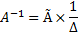
Решение линейных систем с помощью обратных матриц в общем виде и на примере.

Решением называется всякий упорядоченный набор значений, при этом сами значения 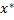( 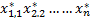) , который подставленный в любой из уравнений системы превратит его в верное числ. равенство. При этом сами значения 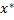называются координатами