Равномерный закон распределения.
Часто на практике мы имеем дело со случайными величинами, распределенными определенным типовым образом, то есть такими, закон распределения которых имеет некоторую стандартную форму. В прошлой лекции были рассмотрены примеры таких законов распределения для дискретных случайных величин (биномиальный и Пуассона). Для непрерывных случайных величин тоже существуют часто встречающиеся виды закона распределения, и в качестве первого из них рассмотрим равномерный закон.
Закон распределения непрерывной случайной величины называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение ( f(x) = const при a ≤ x ≤ b, f(x) = 0 при x < a, x > b.
Найдем значение, которое принимает f(x) при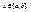 
Из условия нормировки следует, что 
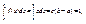откуда 
.
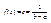Вероятность попадания равномерно распределенной случайной величины на интервал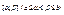 
равна при этом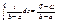 
Вид функции распределения для нормального закона: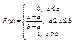 
Другие виды распределений
Биномиальное распределение.
Для дискретной случайной величины Х, представляющей собой число появлений события А в серии из п независимых испытаний (см. лекцию 6), М(Х) можно найти, используя свойство 4 математического ожидания. Пусть Х1 – число появлений А в первом испытании, Х2 – во втором и т.д. При этом каждая из случайных величин Хi задается рядом распределения вида
| Xi | ||
| pi | q | p |
Следовательно, М(Хi) = p. Тогда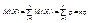 
Аналогичным образом вычислим дисперсию: D(Xi) = 0²·q + 1²·p – p²= p – p² = p(1 – p), откуда по свойству 4 дисперсии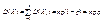 
Закон больших чисел. Предельные теоремы. Неравенство Чебышева. Теоремы Чебышева. Теорема Бернулли.
Изучение статистических закономерностей позволило установить, что при некоторых условиях суммарное поведение большого количества случайных величин почти утрачи-вает случайный характер и становится закономерным (иначе говоря, случайные отклоне-ния от некоторого среднего поведения взаимно погашаются). В частности, если влияние на сумму отдельных слагаемых является равномерно малым, закон распределения суммы приближается к нормальному. Математическая формулировка этого утверждения дается в группе теорем, называемой законом больших чисел.
Неравенство Чебышева.
Неравенство Чебышева, используемое для доказательства дальнейших теорем, справед-ливо как для непрерывных, так и для дискретных случайных величин. Докажем его для дискретных случайных величин.
Неравенство Чебышева.
p( | X – M(X)| < ε ) ≥ D(X) / ε². (13.1)
Доказательство. Пусть Х задается рядом распределения
| Х | х1 | х2 | … | хп |
| р | р1 | р2 | … | рп |
Так как события |X – M(X)| < ε и |X – M(X)| ≥ ε противоположны, то р ( |X – M(X)| < ε ) + + р ( |X – M(X)| ≥ ε ) = 1, следовательно, р ( |X – M(X)| < ε ) = 1 - р ( |X – M(X)| ≥ ε ). Найдем р ( |X – M(X)| ≥ ε ).
D(X) = (x1 – M(X))²p1 + (x2 – M(X))²p2 + … + (xn – M(X))²pn . Исключим из этой суммы те слагаемые, для которых |X – M(X)| < ε. При этом сумма может только уменьшиться, так как все входящие в нее слагаемые неотрицательны. Для определенности будем считать, что отброшены первые k слагаемых. Тогда
D(X) ≥ (xk+1 – M(X))²pk+1 + (xk+2 – M(X))²pk+2 + … + (xn – M(X))²pn ≥ ε² (pk+1 + pk+2 + … + pn).
Отметим, что pk+1 + pk+2 + … + pn есть вероятность того, что |X – M(X)| ≥ ε, так как это сумма вероятностей всех возможных значений Х, для которых это неравенство справедливо. Следовательно, D(X) ≥ ε² р(|X – M(X)| ≥ ε), или р (|X – M(X)| ≥ ε) ≤ D(X) / ε². Тогда вероятность противоположного события p( | X – M(X)| < ε ) ≥ D(X) / ε², что и требо-валось доказать.