Тема 5.1. Понятие величины и ее измерения

План лекции:

1.. Понятие положительной скалярной величины и ее измерения

2.Основные положения, связанные с однородными величинами

3.Измерение величин

Введение.

Известно, что числа возникли из потребности счета и из­мерения, но если для счета достаточно натуральных чисел, то для измерения величин нужны и другие числа. Однако в каче­стве результата измерения величин будем рассматривать только натуральные числа. Определив смысл натурального числа как меры величины, мы выясним, какой смысл имеют арифметические действия над такими числами. Эти знания нужны учителю начальных классов не только для обоснова­ния выбора действий при решении задач с величинами, но и для понимания еще одного подхода к трактовке натурального числа, существующего в начальном обучении математике.

Натуральное число мы будем рассматривать в связи с из­мерением положительных скалярных величин - длин, площа­дей, масс, времени и др., поэтому прежде, чем говорить о взаимосвязи величин и натуральных чисел, напомним некоторые факты, связанные с величиной и ее измерением, тем более что понятие величины, наряду с числом, является основным в начальном курсе математики.

1. . Понятие положительной скалярной величины и ее измерения

Рассмотрим два высказывания, в которых используется слово «длина»:

1)Многие окружающие нас предметы имеют длину.

2) Стол имеет длину.

В первом предложении утверждается, что длиной облада­ют объекты некоторого класса. Во втором речь идет о том, что длиной обладает конкретный объект из этого класса. Обобщая, можно сказать, что термин «длина» употребляется для обозначения свойства, либо класса объектов (предметы имеют длину), либо конкретного объекта из этого класса (стол имеет длину).

Но чем это свойство отличается от других свойств объек­тов этого класса? Так, например, стол может иметь не только длину, но и быть изготовленным из дерева или металла; столы могут иметь разную форму. О длине можно сказать, что раз­ные столы обладают этим свойством в разной степени (один стол может быть длиннее или короче другого), чего не ска­жешь о форме - один стол не может быть «прямоугольнее» другого.

Таким образом, свойство «иметь длину» - особое свойство объектов, оно проявляется тогда, когда объекты сравнивают по их протяженности (по длине). В процессе сравнения уста­навливают, что-либо два объекта имеют одну и ту же длину, либо длина одного меньше длины другого.

Аналогично можно рассматривать и другие известные ве­личины: площадь, массу, время и т.д. Они представляют собой особые свойства окружающих нас предметов и явлений и про­являются при сравнении предметов и явлений по этому свой­ству, причем каждая величина связана с определенным спосо­бом сравнения.

Величины, которые выражают одно и тоже свойство объ­ектов, называются величинами одного рода или однородными величинами: Например, длина стола и длина комнаты - это величины одного рода.

Напомним основные положения, связанные с однородны­ми величинами.

1. Любые две величины одного рода сравнимы: они либо равны, либо одна меньше другой. Другими словами, для величин одного рода имеют место отношения «равно», «мень-
ше» и «больше», и для любых величин А и В справедливо одно и только одно из отношений: А < В, А = В, А > В.

Например, мы говорим, что длина гипотенузы прямо­угольного треугольника больше, чем длина любого катета этого треугольника, масса яблока меньше массы арбуза, а длины противоположных сторон прямоугольника равны.

2. Отношение «меньше» для однородных величин транзитивно: если А < В и В < С, то А < С.

Так, если площадь треугольника F₁ меньше площади тре­угольника F₂, и площадь треугольника F₂ меньше площади треугольника F₃, то площадь треугольника F1 меньше площа­ди треугольника F₃.

3. Величины одного рода можно складывать, в результате
сложения получается величина того же рода. Иными словами,
для любых двух величин А и В однозначно определяется вели-
чина С = А + В, которую называют суммой величин А и В.

Величины, как свойства объектов, обладают еще одной особенностью - их можно оценивать количественно. Для этого величину надо измерить. Чтобы осуществить измере­ние из данного рода величин выбирают величину, которую называют единицей измерения. Мы будем обозначать ее буквой Е.

Если задана величина А и выбрана единица величины Е (того же рода), то измерить величину А - это значит найти такое положительное действительное число х, что А = х/Е.

Число х называется численным значением величины А при единице величины Е. Оно показывает, во сколько раз вели­чина А больше (или меньше) величины Е, принятой за еди­ницу измерения.

Если А = х/Е, то число х называют также мерой величины А при единице Е и пишут х = тЕ(А).

Например, если А ~ длина отрезка а, Е - длина отрезка b (рис. 118), то А = 4/Е. Число 4- это численное значение дли­ны А при единице длины Е, или, другими словами, число 4-это мера длины А при единице длины Е.

В практической деятельности при измерении величин люди пользуются стандартными единицами величин: так, длину измеряют в метрах, сантиметрах и т.д. Результат измерения записывают в таком виде: 2,7 кг; 13 см; 16 с. Исходя из поня­тия измерения, данного выше, эти записи можно рассматри­вать как произведение числа и единицы величины. Например, 2,7 кг = 2,7-кг; 13 см = 13-см; 16 с = 16 с.

Используя это представление, можно обосновать процесс перехода от одной единицы величины к другой. Пусть, напри­мер, требуется выразить 1\4ч в минутах. Так как1 ч = 60 и

час = 60 мин, то 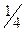ч = 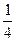*60-мин = = 25 мин.

Величина, которая определяется одним численным значе­нием, называется скалярной величиной.

Если при выбранной единице измерения скалярная вели­чина принимает только положительные численные значения, то ее называют положительной скалярной величиной.

Положительными скалярными величинами являются дли­на, площадь, объем, масса, время, стоимость и количество товара и др.

Измерение величин позволяет переходить от сравнения ве­личин к сравнению чисел, от действий над величинами к соот­ветствующим действиям над числами, и наоборот.

В математике при записи произведения величины А на чис­ло х принято число писать перед величиной, т.е. х*А. Но раз­решается писать и так: А*х. Тогда численное значение вели­чины А умножают на х, если находят значение величины А-х.

Рассмотренные понятия - объект (предмет, явление, про­цесс), его величина, численное значение величины, единица величины - надо уметь вычленять в текстах и задачах. Напри­мер, математическое содержание предложения «Купили 3 кило­грамма яблок» можно описать следующим образом: в предложении рассматривается такой объект, как яблоки, и его свойст­во - масса; для измерения массы использовали единицу массы -килограмм; в результате измерения получили число 3 - числен­ное значение массы яблок при единице массы - килограмм.

Один и тот же объект может обладать несколькими свой­ствами, которые являются величинами. Например, для чело­века- это рост, масса, возраст и др. Процесс равномерного движения характеризуется тремя величинами: расстоянием, скоростью и временем, между которыми существуют зависи­мость, выражаемая формулой S=V/t

Если величины выражают разные свойства объекта, то их называют величинами разного рода, или разнородными величина­ми. Так, например, длина и масса - это разнородные величины.