Основные определения метода конечных элементов

Метод конечных элементов (МКЭ) - основной метод современной строительной механики, лежащий в основе подавляющего большинства современных программных комплексов, предназначенных для выполнения расчетов строительных конструкций на ЭВМ.

Но диапазон его применения чрезвычайно широк: строительство и машиностроение, гидро- и аэродинамика, горное дело и новейшая техника, а также различные задачи математической физики – теплопроводности, фильтрации, распространения волн и т. д.

Метод конечных элементов, как и многие другие численные методы, основан на представлении реальной континуальной конструкции ее дискретной моделью и замене дифференциальных уравнений, описывающих НДС сплошных тел, системой алгебраических уравнений. Вместе с тем МКЭ допускает ясную геометрическую, конструктивную и физическую интерпретацию.

Суть метода заключается в том, что область (одно- , двух- или трехмерная), занимаемая конструкцией, разбивается на некоторое число малых, но конечных по размерам подобластей (рис. 1). Последние носят название конечных элементов (КЭ), а сам процесс разбивки – дискретизацией.

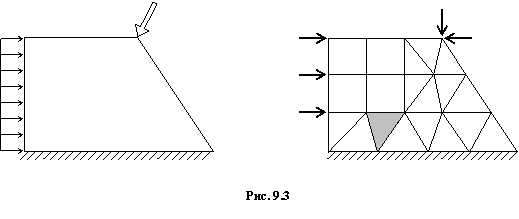
В зависимости от типа конструкции и характера ее деформации КЭ могут иметь различную форму. Так, при расчете стержневых систем (фермы, балки, рамы) КЭ представляют собой участки стержней; для двумерных континуальных конструкций (пластины, плиты, оболочки) чаще всего применяют треугольные и прямоугольные (плоские или изогнутые) КЭ; а для трехмерных областей (толстые плиты, массивы) – КЭ в форме тетраэдра или параллелепипеда. В отличие от реального сооружения в дискретной модели конечные элементы связываются между собой только в отдельных точках (узлах) определенным конечным числом узловых параметров.

МКЭ – это вариационный метод. Функционал энергии для всей рассматриваемой области здесь представляется в виде суммы функционалов отдельных ее частей – конечных элементов. По области каждого элемента, независимо от других, задается свой закон распределения искомых функций. Такая кусочно-непрерывная аппроксимация выполняется с помощью специально подобранных аппроксимирующих функций, называемых также координатными или интерполирующими. С их помощью искомые непрерывные величины (перемещения, напряжения и т.д.) в пределах каждого КЭ выражаются через значения этих величин в узловых точках, а произвольная заданная нагрузка заменяется системой эквивалентных узловых сил.

При такой кусочно-непрерывной аппроксимации обеспечивается условие совместности лишь в узлах, а в остальных точках по границам КЭ это условие удовлетворяется в общем случае приближенно (в связи с этим различают КЭ разной степени совместности).

Наибольшее распространение получил метод конечных элементов в перемещениях, имеющий много общего с методом Ритца и вариационно-разностным методом (в дальнейшем мы будем в основном рассматривать именно этот вариант МКЭ). Различие между традиционной схемой метода Ритца и МКЭ в форме метода перемещений заключается в выборе системы аппроксимирующих функций. Если в методе Ритца аппроксимация перемещений производится по всей области их определения, то в МКЭ – по каждому конечному элементу в отдельности, что позволяет использовать аппроксимирующие функции более простого вида. В первом случае функционал полной потенциальной энергии варьируется по неопределенным коэффициентам 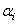, во втором – по перемещениям в узлах сетки, что приводит к системе алгебраических уравнений метода перемещений (основными неизвестными являются непосредственно узловые перемещения). При этом использование кусочно-непрерывной аппроксимации позволяет получить редко заполненную или ленточную структуру матрицы коэффициентов системы уравнений и таким образом дает возможность применения более эффективных методов ее решения.

Число узлов и число перемещений в узле (степень свободы узла), принятые для конечного элемента, могут быть различными, однако не должны быть меньше минимально необходимых для описания напряженно-деформированного состояния КЭ в рамках принятой физической модели. Число независимых перемещений во всех узлах элемента определяет степень свободы КЭ. Степень свободы всей конструкции и соответственно порядок системы разрешающих уравнений определяется суммарным числом перемещений всех ее узлов. Поскольку основными неизвестными МКЭ в форме метода перемещений считаются узловые перемещения, степень свободы КЭ и всей конструкции в целом является чрезвычайно важным понятием в МКЭ. Понятия о степени свободы узла, КЭ и конструкции и степени их же кинематической неопределимости идентичны.

Способ разбивки рассматриваемой области на конечные элементы, их число и число степеней свободы, а также вид аппроксимирующих функций в конечном итоге предопределяют точность расчета конструкции. Следует отметить, что простым увеличением числа конечных элементов не всегда удается достичь повышения точности расчетов. Вопросы устойчивости и сходимости решения, а также оценки точности полученных результатов являются основными при использовании МКЭ.

По сравнению с другими численными методами МКЭ в лучшей степени алгоритмизирован и более гибок при описании геометрии и граничных условий рассчитываемой области. Кроме того, к достоинствам метода следует отнести его физическую наглядность и универсальность.

Применительно к стержневым системам МКЭ в форме метода перемещений может рассматриваться как матричная форма классического метода перемещений, отличающаяся только более глубокой формализацией алгоритма и ориентацией его на использование ЭВМ.

Метод конечных элементов позволяет практически полностью автоматизировать расчет стержневых систем, хотя, как правило, требует выполнения значительно большего числа вычислительных операций по сравнению с классическими методами строительной механики. Однако, в современных условиях большой объем вычислений не является серьезной проблемой, и, в связи с этим, при внедрении ЭВМ в инженерную практику МКЭ получил широчайшее распространение. Поэтому, знание основ метода конечных элементов и современных программных средств, позволяющих на его основе решать разнообразные задачи, в наше время для инженера является абсолютно необходимым.

Виды МКЭ

По способу получения основных, т. е. разрешающих, уравнений различают четыре основных вида метода конечных элементов: прямой, вариационный, взвешенных невязок и энергетического баланса.

Прямой метод аналогичен матричному методу перемещений для стержневых систем, в основе его лежат положения, которые использовались на ранней стадии развития МКЭ. Этот метод удобен своей простотой и очевидным геометрическо-физическим значением отдельных шагов аппроксимации. Соотношения для КЭ здесь строятся непосредственно на основе трех групп уравнений (трех сторон задачи): статической, геометрической и физической. Однако область применения прямого метода весьма ограничена: его можно использовать лишь для конечных элементов простой геометрии с малым числом степеней свободы в узле.

Вариационный метод основан на принципах стационарности некоторой переменной, зависящей от одной или нескольких функций (такая переменная носит название функционала). Применительно к механике деформируемого твердого тела эта переменная представляет собой потенциальную (функционал Лагранжа) или дополнительную (функционал Кастилиано) энергию системы или формируется на основе этих двух энергий (функционалы Хеллингера-Рейсснера, Ху-Вашицу). Если в функционал подставить аппроксимирующие выражения искомых функций и применить к нему экстремальные принципы (соответственно принцип Лагранжа, принцип Кастилиано и т. д.), получим систему алгебраических уравнений, решением которой будут значения узловых неизвестных. В отличие от прямого вариационный метод может одинаково успешно применяться как к простым, так и сложным задачам.

Метод невязок представляет собой наиболее общий подход к построению основных соотношений МКЭ. Этот метод целесообразно применять при решении задач, у которых трудно или невозможно сформулировать вариационное уравнение, т.е. функционал. Суть метода взвешенных невязок заключается во введении некоторой невязки – отклонении приближенного аппроксимативного решения от точного решения дифференциальных уравнений для данной задачи. Чтобы получить ”наилучшее” решение, необходимо минимизировать некоторый интеграл от невязок по расчетной области. Для повышения эффективности в подынтегральное выражение наряду с самой невязкой обычно вводится так называемая весовая функция, в этом случае метод называется методом взвешенных невязок. Выбор схемы минимизации и весовых функций определяет различные варианты метода невязок. Наиболее часто применяемые из них – это метод Галеркина, который приводит к тем же уравнениям, что и вариационный подход, а также метод наименьших квадратов.

Метод энергетического баланса (метод Одена) основан на балансе различных видов энергии, записанном в интегральной форме. Этот метод успешно применяется при решении нелинейных и динамических задач.

Из приведенных видов МКЭ в строительной механике особенно актуальны вариационный метод и метод взвешенных невязок Галеркина, которые для рассматриваемой задачи представляют собой два взаимно дополняющих метода одинаковой точности. Широкое применение этих методов обусловлено тем, что выражения в функционале или во взвешенном интеграле, как правило, имеют низший порядок производных по сравнению с производными в соответствующем дифференциальном уравнении для данной задачи. Это позволяет выбирать аппроксимирующие функции из более широкого семейства простых функций. Можно сказать, что вариационный вид МКЭ вышел из классического метода Ритца, а метод Галеркина – из обобщенного метода Бубнова-Галеркина. В принципе, из других методов также выводятся соответствующие виды МКЭ, однако их применяют значительно реже.

Формы МКЭ

В МКЭ, аналогично классическим методам строительной механики, за основные неизвестные могут приниматься величины разного типа: кинематические (перемещения, деформации), статические (внутренние силы, напряжения и др.) или смешанные кинематические и статические параметры. В зависимости от выбора узловых неизвестных различают три формы МКЭ: метод перемещений, метод сил и смешанный метод. С этой точки зрения МКЭ можно рассматривать как обобщение традиционных методов строительной механики стержневых систем применительно к расчету континуальных систем.

Метод перемещений – в настоящее время наиболее распространенная форма МКЭ. Это объясняется тем, что для заданной конструкции легче получить кинематически определимую основную систему метода перемещений, нежели статически определимую основную систему метода сил. Кроме того, матрица жесткости метода перемещений составляется без особых затруднений и, как правило, имеет разряженную или ленточную структуру.

В основе математической формулировки МКЭ в форме метода перемещений лежит вариационный принцип Лагранжа, т. е. принцип минимума потенциальной энергии системы. Основными неизвестными здесь являются перемещения узловых точек дискретной схемы, напряжения же вторичны и определяются путем численного дифференцирования перемещений.

К достоинствам метода относятся: простота реализации; удовлетворительные точность и устойчивость решения с гарантированной сходимостью к нижней границе. Минусы: точность определения напряжений намного ниже, чем перемещений, хотя именно значения напряжений важны при прочностных расчетах, к тому же поскольку приближенное решение отвечает нижней границе, то значения и перемещений, и напряжений оказываются заниженными.

Принцип минимума дополнительной энергии и связанные с ним схемы МКЭ в форме метода сил, а также вариационный принцип Рейсснера (смешанный метод) не получили такого широкого распространения. Однако во многих случаях они могут быть эффективны, особенно в отношении вычисления напряжений. К тому же выполнение двойственных расчетов на основе альтернативных форм МКЭ позволяет, как правило, получить двухстороннюю оценку точного решения соответствующей задачи.

Главным плюсом МКЭ в форме метода сил является то, что основные неизвестные здесь – напряжения. И если бы в реализации метода сил не было определенных сложностей, значения напряжений можно было получать той же степени точности, что и перемещения в методе перемещений. Кроме того, использование принципа Кастилиано дает верхнюю границу приближенного решения (т. е. напряжения завышены), что в принципе лучше при расчетах на прочность, нежели заниженная оценка. Тем не менее, пока нет алгоритмов, в той же степени простых и устойчивых, имеющих гарантированную сходимость в обширном классе задач, подобно МКЭ в форме метода перемещений.

В основе вариационной формулировки смешанного метода лежит принцип стационарности различных форм функционала Рейсснера. При данном подходе перемещения и напряжения в пределах каждого КЭ аппроксимируются одновременно, поэтому нет необходимости завышать требования к непрерывности искомых функций и их производных. Напротив, можно задавать именно нужные аппроксимации, а поскольку смешанные вариационные принципы приводят и к смешанному виду соотношений между напряжениями и перемещениями для конечного элемента, можно получать более точное решение.

Однако имеются и большие минусы. Так, функционал Рейсснера не является выпуклым, поверхность его в точке стационарности имеет вырожденную седлообразную форму. Система разрешающих уравнений, отвечающая формулировке смешанного метода, не является положительно определенной. Эти обстоятельства значительно затрудняют прямое использование функционала Рейсснера в методе конечных элементов.

Также существуют различные гибридные формы как метода перемещений, так и метода сил. По сути гибридные подходы схожи со смешанным методом. Отличает их то, что в гибридных моделях внутри конечного элемента за основные неизвестные принимаются величины одного типа, а на границах элемента независимо и в другой форме – величины другого или же обоих типов.

Как правило, гибридные формулировки приводят к значительному усложнению алгоритма, поэтому эффективны лишь для ограниченного класса задач. Например, если в гибридном методе сил внутри элемента задать аппроксимацию компонент напряжений, в традиционной форме метода сил это бы привело к решению, соответствующему верхней границе. Однако аппроксимация перемещений вдоль контура элемента накладывает некоторые ограничения на математическую модель, уменьшает податливость и тем самым смещает получаемое решение в сторону точного. Сложность в том, что имеется возможность перегрузить ограничениями функционал дополнительной энергии и легко проскочить точное решение в сторону нижней границы.

Аппроксимация

МКЭ относится к методам дискретного анализа. Однако в отличие от численных методов, основывающихся на математической дискретизации дифференциальных уравнений, МКЭ базируется на физической дискретизации рассматриваемого объекта. Реальная конструкция как сплошная среда с бесконечно многим числом степеней свободы заменяется дискретной моделью связанных между собой элементов с конечным числом степеней свободы. Так как число возможных дискретных моделей для континуальной области неограниченно велико, то основная задача заключается в том, чтобы выбрать такую модель, которая лучше всего аппроксимирует данную область.

Сущность аппроксимации сплошной среды по МКЭ состоит в следующем:

1) рассматриваемая область разбивается на определенное число КЭ, семейство элементов по всей области называется системой или сеткой конечных элементов;

2) предполагается, что КЭ соединяются между собой в конечном числе точек – узлов, расположенных по контуру каждого из элементов;

3) искомые функции в пределах каждого КЭ (например, распределение перемещений, деформаций, напряжений и т. д.) с помощью аппроксимирующих функций выражаются через узловые значения, представляющие собой основные неизвестные МКЭ;

4) для анализа и расчета полученной системы конечных элементов действительны все принципы и методы, применяемые для любых дискретных систем.