Комплексные числа, действия над ними
Алгебраическое уравнение 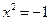 не имеет решений на множестве действительных чисел. Этот факт подводит нас к необходимости расширения понятия числа.
не имеет решений на множестве действительных чисел. Этот факт подводит нас к необходимости расширения понятия числа.
Определение 1. Комплексными числами называются числа вида  , где
, где 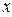 ,
, 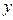 являются действительными числами, а
являются действительными числами, а 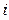 - условный символ. При этом введены операции сложения и умножения по следующим правилам.
- условный символ. При этом введены операции сложения и умножения по следующим правилам.
Пусть заданы 2 комплексных числа 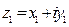 и
и 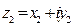 , тогда их сумма и произведения определяются формулами:
, тогда их сумма и произведения определяются формулами:
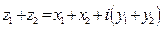 ,
, 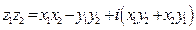 . (1)
. (1)
Обратите внимание, что определение не только вводит новый объект – множество 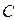 комплексных чисел вида
комплексных чисел вида  . Также введены операции над этими числами – сложение и умножение. По определению, они выполняются по формулам (1). Как запомнить формулы (1) и в чем смыл символа «
. Также введены операции над этими числами – сложение и умножение. По определению, они выполняются по формулам (1). Как запомнить формулы (1) и в чем смыл символа « 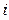 »? По сути, мы обычным образом раскрываем скобки при проведении арифметических операций и при этом квадрат условного символа
»? По сути, мы обычным образом раскрываем скобки при проведении арифметических операций и при этом квадрат условного символа 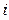 заменяем числом
заменяем числом 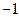 .
.
Для числа  число
число 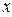 называется действительной частью, а число
называется действительной частью, а число 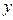 - мнимой частью этого комплексного числа. При этом используются обозначения
- мнимой частью этого комплексного числа. При этом используются обозначения 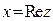 ,
, 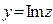 . Два комплексных числа называются сопряженными, если их действительные части равны, а мнимые отличаются знаком. В общем виде парой сопряженных комплексных чисел являются числа
. Два комплексных числа называются сопряженными, если их действительные части равны, а мнимые отличаются знаком. В общем виде парой сопряженных комплексных чисел являются числа  и
и 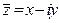 .
.
Числа 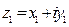 и
и 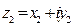 равны тогда о только тогда, когда совпадают их действительные и мнимые части, т.е. выполнены равенства:
равны тогда о только тогда, когда совпадают их действительные и мнимые части, т.е. выполнены равенства: 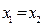
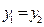 . Если мнимая часть комплексного числа равна 0, то это число принадлежит множеств действительных чисел
. Если мнимая часть комплексного числа равна 0, то это число принадлежит множеств действительных чисел 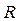 Иными словами, множество действительных чисел содержится в множестве комплексных чисел, что можно записать в виде
Иными словами, множество действительных чисел содержится в множестве комплексных чисел, что можно записать в виде 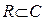 .
.
Про комплексные числа нельзя сказать, что одно из них больше или меньше другого. В этом смысле их нельзя сравнивать. Можно лишь ответить на вопрос, равны или не равны два таких числа.
Комплексное число равно 0 тогда и только тогда, когда равны 0 его действительная и мнимая части. Справедливо равенство 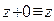 и таким свойством обладает лишь число 0.
и таким свойством обладает лишь число 0.
Комплексное число равно 1 тогда и только тогда, когда его действительная часть равна 1, а мнимая часть равна 0. Справедливо равенство 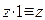 и таким свойством обладает лишь число 1.
и таким свойством обладает лишь число 1.
В определении даются формулы для сложения и умножения комплексных чисел. Это автоматически порождает ряд дополнительных операций над комплексными числами. Под вычитанием понимается действие, обратное сложению. Поэтому для чисел 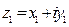 и
и 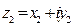 справедлива формула
справедлива формула 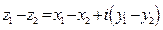 . Умножение комплексного числа
. Умножение комплексного числа  на действительное число
на действительное число 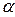 является частным случаем перемножения комплексных чисел, поэтому справедлива формула
является частным случаем перемножения комплексных чисел, поэтому справедлива формула 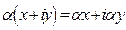 . Под делением понимается действие, обратное умножению. Заметим, что для чисел
. Под делением понимается действие, обратное умножению. Заметим, что для чисел 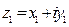 и
и 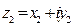 справедливо соотношение
справедливо соотношение 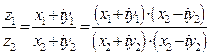 . После раскрытия скобок получим формулу
. После раскрытия скобок получим формулу 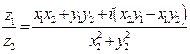 .
.
Пример 1. Даны комплексные числа 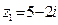 ,
, 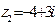 . Вычислите:
. Вычислите:
а) 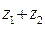 , б)
, б) 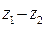 , в)
, в) 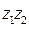 , г)
, г) 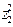 , д)
, д) 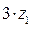 , е)
, е) 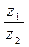 ж)
ж) 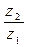 .
.
Решение. В первых 5 пунктах действуем по определению:
а) 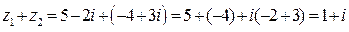 ;
;
б) 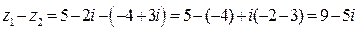 ;
;
в) 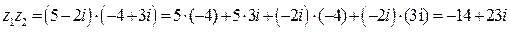 ;
;
г) 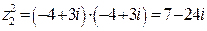 ; д)
; д) 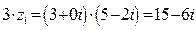 .
.
Переходим к последним двум пунктам. Еще раз ответим на вопрос, как поделить 2 комплексных числа? При вычислении в п.. е) 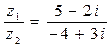 можно рассмотреть уравнение
можно рассмотреть уравнение 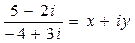 или
или 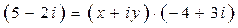 . Раскрывая скобки, приравнивая действительные и мнимые части, мы получим однозначно разрешимую систему для определения неизвестных
. Раскрывая скобки, приравнивая действительные и мнимые части, мы получим однозначно разрешимую систему для определения неизвестных 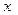 и
и 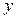 . Тем самым частное будет найдено.
. Тем самым частное будет найдено.
На самом деле, есть более простой способ деления комплексных чисел. Заметим, что если комплексное число умножить на сопряженное, то получится действительное число, т.е. 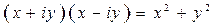 . Отсюда
. Отсюда 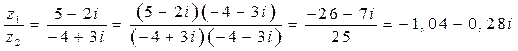 . Также
. Также 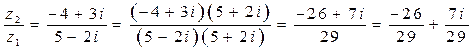 .
.
