Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых функций. Эквивалентные функции и их применение к вычислению пределов
Бесконечно большая функция (б.б.ф)
Функция y = f (x) называется бесконечно большой при х→ х0, если для любого числа М > 0 существует число δ = δ (М) > 0, что для всех х, удовлетворяющих неравенству 0 < |х-  х0| < δ, выполняется неравенство |f(х)| > М. Записывают
х0| < δ, выполняется неравенство |f(х)| > М. Записывают 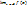 = ∞ или f (x) → ∞ при х → х0.
= ∞ или f (x) → ∞ при х → х0.
Если f(х) стремится к бесконечности при х → х0 и принимает лишь положительные значения, то пишут 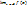 = + ∞; если лишь отрицательные значения, то
= + ∞; если лишь отрицательные значения, то 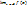 = - ∞.
= - ∞.
Бесконечно малая функция (б.м.ф.)
Функция у = f(x) называется бесконечно малой при х→ х0, если 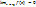 . По определению предела функции равенство означает: для любого числа ɛ > 0 найдется число δ > 0 такое, что для всех х, удовлетворяющих неравенству 0 < |х – х0| < δ, выполняется неравенство |f (x)| < ɛ.
. По определению предела функции равенство означает: для любого числа ɛ > 0 найдется число δ > 0 такое, что для всех х, удовлетворяющих неравенству 0 < |х – х0| < δ, выполняется неравенство |f (x)| < ɛ.
Аналогично определяется б.м.ф. при х→ х0 + 0, х→ х0 – 0, х→ + ∞, х→ - ∞: во всех этих случаях f (x) →0.
Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми; обозначают обычно греческими буквами α, β и т.д.
Сравнение бесконечно малых функций
Как известно, сумма, разность и произведение двух б.м.ф. есть функция бесконечно малая. Отношение же двух б.м.ф. может вести себя различным образом: быть конечным числом, быть бесконечно большой функцией, бесконечно малой или вообще не стремиться ни к какому пределу.
Две б.м.ф.сравниваются между собой с помощью их отношения.
Пусть α = α(х) и β = β(х) есть б.м.ф. при х → х0, т.е. 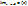 = 0 и
= 0 и 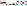 = 0.
= 0.
1.если 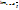 = А ≠ 0 (А ? R), то α и β называются бесконечно малыми одного порядка.
= А ≠ 0 (А ? R), то α и β называются бесконечно малыми одного порядка.
2.если 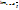 = 0, то α называется бесконечно малой более высокого порядка, чем β.
= 0, то α называется бесконечно малой более высокого порядка, чем β.
3если 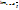 = ∞, то α называется бесконечно малой более низкого порядка, чем β.
= ∞, то α называется бесконечно малой более низкого порядка, чем β.
4.если 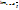 не существует, то α и β называются несравнимыми бесконечно малыми.
не существует, то α и β называются несравнимыми бесконечно малыми.
Отметим, что такое же правило сравнения б.м.ф.при х → ± ∞, х → х0 ± 0.
Эквивалентные функции
Среди бесконечно малых функций одного порядка особую роль играют так назывемые эквивалентные бесконечно малые.
Если 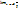 = 1, то α и β называются эквивалентными бесконечно малыми (при х → х0); это обозначается так: α ~ β.
= 1, то α и β называются эквивалентными бесконечно малыми (при х → х0); это обозначается так: α ~ β.
Применение эквивалентных функций для вычисления пределов
Для раскрытия неопределенностей вида  часто бывают полезным применять принцип замены бесконечно малых эквивалентными и другие свойства эквивалентных бесконечно малых функций. Как известно, sin x ~ х при х → 0, tg х ~ х при х → 0.
часто бывают полезным применять принцип замены бесконечно малых эквивалентными и другие свойства эквивалентных бесконечно малых функций. Как известно, sin x ~ х при х → 0, tg х ~ х при х → 0.
важнейшие эквивалентности, которые используют для вычисления пределов:
1) sin х ~ х при х → 0;
2) tg х ~ х (х → 0);
3) arcsin х ~ х (х → 0);
4) arctg х ~ х (х → 0);
5) 1 – cos х ~ 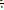 (х → 0);
(х → 0);
6)  - 1 ~ х (х → 0);
- 1 ~ х (х → 0);
7)  - 1 ~ х * ln а (х → 0);
- 1 ~ х * ln а (х → 0);
8) ln (1+х) ~ х (х → 0);
9) 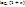 ~ х *
~ х * 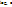 (х → 0);
(х → 0);
10) (1 + х)k – 1 ~ k * х, k > 0 (х → 0);
в частности, 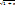 - 1 ~
- 1 ~  .
.
40ВОПРОС Непрерывность функции в точке и на отрезке. Свойства функций, непрерывных в точке.
Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точкех0, если предел функции и ее значение в этой точке равны, т.е.
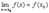 Тот же факт можно записать иначе:
Тот же факт можно записать иначе:
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).
