МИНИСТЕРСТВО ОБРАЗОВАНИЯ САРАТОВСКОЙ ОБЛАСТИ 6 страница. Определяем значения поперечной силы Q в характерных сечениях балки, которые обозначены 1, А, В,5 (рис

F q

m

рис.а 1 А 2 3 4 В 5

1 3 3 2

рис.б Эпюра Q

(кН)

рис.в Эпюра М

(МПа)

Определяем значения поперечной силы Q в характерных сечениях балки, которые обозначены 1, А, В,5 (рис. а).

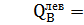
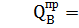
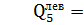
По найденным значениям строим эпюру поперечных сил Q (рис. б).

Для построения эпюры на участке (b+c) достаточно было определить поперечную силу в точках А и В, так как эпюра на этом участке описывается прямой линией.

Так как эпюра пересекает нулевую линию в т.С, необходимо определить абсциссу сечения (расстояние z_o). Для этого ординату в начале распределенной нагрузки (Q_A) делим на интенсивность распределенной нагрузки:

3. Определяем значения изгибающих моментов М в характерных сечениях балки:

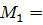
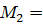
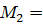
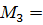
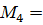
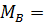
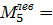
По найденным значениям строим эпюру изгибающих моментов М (рис. в). Строим эпюру на растянутом волокне и знаки на эпюре не ставятся.

4. По эпюре изгибающих моментов определяем положение опасного сечения балки (сечения, в котором изгибающий момент имеет наибольшее по абсолютной величине значение). В нашем случае – это сечение… , где М_… = М _max = …..

Из условия прочности балки на изгиб

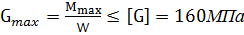
вычисляем необходимый осевой момент сопротивления:

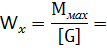
В соответствии с ГОСТ 8239-89 (приложение 1), принимаем сечение из стального двутавра № …… с W = …….

Поверяем:

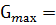
Прочность обеспечена.

5.Проверяем прочность балки по касательным напряжениям. Касательное напряжение вычисляем по формуле Д.И.Журавского

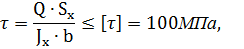
где Q = ……. - максимальное значение Q на эпюре;

S_x= ……. см₃= мм³;

𝐽_x= ……. см⁴= мм⁴;

b=d=…..мм.

Прочность обеспечена.

Ответ: сечение балки двутавр №…… .

ВАРИАНТ № 27

Построить эпюры поперечных сил (Q) и изгибающих моментов (М), подобрать сечение стального двутавра и определить в подобранном сечении максимальное касательное напряжение. Принять [ σ ] = 160 МПа.

Дано:

F = 20 кН; q = 20кН/м; m = 10 кН м; a = 2,0 м; b = 2,0 м ; c = 2,0 м; d = 1,0 м.

F q

m

a b c d

Определить: Q, M.

Решение.

1. Отбросив опоры, заменим их действие на балку соответствующими реакциями V_A, V_B. Составляем уравнения равновесия параллельной системы сил, из которых определяем опорные реакции балки:

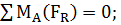……. (1)

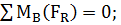…….. (2)

Из уравнения (1) находим V_B:

….

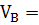Из уравнения (2) находим V_A:

….

Проверяем правильность определения опорных реакций, составляя сумму проекций всех сил на ось Y:

….

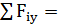т.е. реакции определены верно.

2. Строим расчетную схему и обозначаем на ней характерные точки, по которым будем строить эпюры поперечных сил и изгибающих моментов (рис. а). Под расчетной схемой оставляем место для построения эпюр.

F V_A q V_B

m

рис.а 1 А 2 3 4 В 5

2 2 2 1

рис.б Эпюра Q

(кН)

рис.в Эпюра М

(МПа)

Определяем значения поперечной силы Q в характерных сечениях балки, которые обозначены 1, А, В,5(рис. а).

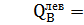
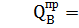
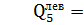
По найденным значениям строим эпюру поперечных сил Q (рис. б).

Для построения эпюры на участке (b+c) достаточно было определить поперечную силу в точках А и В, так как эпюра на этом участке описывается прямой линией.

Так как эпюра пересекает нулевую линию в т.С, необходимо определить абсциссу сечения (расстояние z_o). Для этого ординату в начале распределенной нагрузки (Q_A) делим на интенсивность распределенной нагрузки:

3. Определяем значения изгибающих моментов М в характерных сечениях балки:

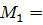
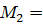
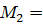
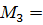
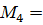
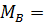
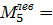
По найденным значениям строим эпюру изгибающих моментов М (рис. в). Строим эпюру на растянутом волокне и знаки на эпюре не ставятся.

4. По эпюре изгибающих моментов определяем положение опасного сечения балки (сечения, в котором изгибающий момент имеет наибольшее по абсолютной величине значение). В нашем случае – это сечение ….., где М….= М _max = …..

Из условия прочности балки на изгиб

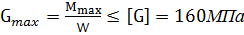
вычисляем необходимый осевой момент сопротивления:

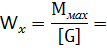
В соответствии с ГОСТ 8239-89 (приложение 1), принимаем сечение из стального двутавра ……с W = ……

Поверяем:

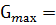
Прочность обеспечена.

5.Проверяем прочность балки по касательным напряжениям. Касательное напряжение вычисляем по формуле Д.И.Журавского

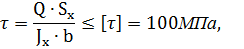
где Q =……. - максимальное значение Q на эпюре;

S_x=……. см₃= мм³;

𝐽_x=…….. см⁴= мм⁴;

b=d=…..мм.

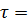
Прочность обеспечена.

Ответ: сечение балки двутавр №…. .

ВАРИАНТ № 28

Построить эпюры поперечных сил (Q) и изгибающих моментов (М), подобрать сечение стального двутавра и определить в подобранном сечении максимальное касательное напряжение. Принять [ σ ] = 160 МПа.

Дано:

F = 40 кН; q = 10кН/м; m = 30 кН м; a = 2,0 м; b = 6,0 м ; c = 1,0 м; d = 1,0 м.

q F

m

a b c d

Определить: Q, M.

Решение.

1. Отбросив опоры, заменим их действие на балку соответствующими реакциями V_A, V_B. Составляем уравнения равновесия параллельной системы сил, из которых определяем опорные реакции балки:

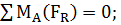……. (1)

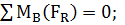…….. (2)

Из уравнения (1) находим V_B:

….

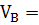Из уравнения (2) находим V_A:

….

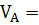Проверяем правильность определения опорных реакций, составляя сумму проекций всех сил на ось Y:

….

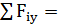т.е. реакции определены верно.

2. Строим расчетную схему и обозначаем на ней характерные точки, по которым будем строить эпюры поперечных сил и изгибающих моментов (рис. а). Под расчетной схемой оставляем место для построения эпюр.

V_B q V_A F

m

рис.а 1 А 2 3 4 5 В 6

2 6 1 1

рис.б Эпюра Q

(кН)

рис.в Эпюра М

(МПа)

Определяем значения поперечной силы Q в характерных сечениях балки, которые обозначены 1, А, 5, В, 6 (рис. а).

=

=

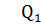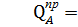
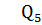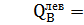
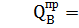
По найденным значениям строим эпюру поперечных сил Q (рис. б).

Для построения эпюры на участке b достаточно было определить поперечную силу в точках А и 5, так как эпюра на этом участке описывается прямой линией.

Так как эпюра пересекает нулевую линию в т.С, необходимо определить абсциссу сечения (расстояние z_o). Для этого ординату в начале распределенной нагрузки (Q_A) делим на интенсивность распределенной нагрузки:

3. Определяем значения изгибающих моментов М в характерных сечениях балки:

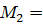
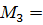
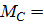
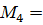
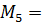
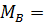
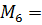
По найденным значениям строим эпюру изгибающих моментов М (рис. в). Строим эпюру на растянутом волокне и знаки на эпюре не ставятся.

4. По эпюре изгибающих моментов определяем положение опасного сечения балки (сечения, в котором изгибающий момент имеет наибольшее по абсолютной величине значение). В нашем случае – это сечение …., где М_….= М _max = …..

Из условия прочности балки на изгиб

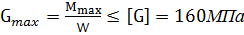
вычисляем необходимый осевой момент сопротивления:

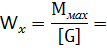
В соответствии с ГОСТ 8239-89 (приложение 1), принимаем сечение из стального двутавра № ……с W = …….

Поверяем:

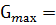
Прочность обеспечена.

5.Проверяем прочность балки по касательным напряжениям. Касательное напряжение вычисляем по формуле Д.И.Журавского

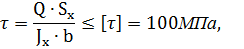
где Q = ….. - максимальное значение Q на эпюре;

S_x= ….. см₃= мм³;

𝐽_x= ….. см⁴= мм⁴;

b=d= …. мм.

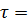
Прочность обеспечена.

Ответ: сечение балки двутавр №…… .

ВАРИАНТ № 29

Построить эпюры поперечных сил (Q) и изгибающих моментов (М), подобрать сечение стального двутавра и определить в подобранном сечении максимальное касательное напряжение. Принять [ σ ] = 160 МПа.

Дано:

F = 50 кН; q = 20кН/м; m =20 кН м; a = 1,0 м; b = 5,0 м ; c = 2,0 м; d = 1,0 м.

q F

m

a b c d

Определить: Q, M.

Решение.

1. Отбросив опоры, заменим их действие на балку соответствующими реакциями V_A, V_B . Составляем уравнения равновесия параллельной системы сил, из которых определяем опорные реакции балки:

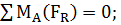……… (1)

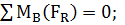………(2)

Из уравнения (1) находим V_B:

….

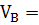Из уравнения (2) находим V_A:

….

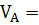Проверяем правильность определения опорных реакций, составляя сумму проекций всех сил на ось Y:

….

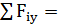т.е. реакции определены верно.

2. Строим расчетную схему и обозначаем на ней характерные точки, по которым будем строить эпюры поперечных сил и изгибающих моментов (рис. а). Под расчетной схемой оставляем место для построения эпюр.

V_A q V_B F

m

рис.а 1 А 2 3 4 5 В 6

рис.б Эпюра Q

(кН)

рис.в Эпюра М

(МПа)

Определяем значения поперечной силы Q в характерных сечениях балки, которые обозначены 1, А, 5, В, 6 (рис. а).

=

=

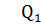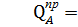
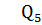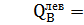
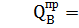
По найденным значениям строим эпюру поперечных сил Q (рис. б).

Для построения эпюры на участке b достаточно было определить поперечную силу в точках А и 5, так как эпюра на этом участке описывается прямой линией.

Так как эпюра пересекает нулевую линию в т.С, необходимо определить абсциссу сечения (расстояние z_o). Для этого ординату в начале распределенной нагрузки (Q_A) делим на интенсивность распределенной нагрузки:

3. Определяем значения изгибающих моментов М в характерных сечениях балки:

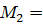
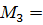
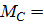
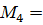
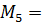
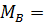
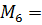
По найденным значениям строим эпюру изгибающих моментов М (рис. в). Строим эпюру на растянутом волокне и знаки на эпюре не ставятся.

4. По эпюре изгибающих моментов определяем положение опасного сечения балки (сечения, в котором изгибающий момент имеет наибольшее по абсолютной величине значение). В нашем случае – это сечение …, где М_….= М _max = …..

Из условия прочности балки на изгиб

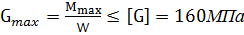
вычисляем необходимый осевой момент сопротивления:

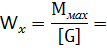
В соответствии с ГОСТ 8239-89 (приложение 1), принимаем сечение из стального двутавра №……с W = …….

Поверяем:

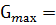
Прочность обеспечена.

5.Проверяем прочность балки по касательным напряжениям. Касательное напряжение вычисляем по формуле Д.И.Журавского

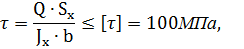
где Q =….. - максимальное значение Q на эпюре;

S_x= ….. см₃= мм³;

𝐽_x= ….. см⁴= мм⁴;

b=d=….. мм.

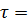
Прочность обеспечена.

Ответ: сечение балки двутавр №.

ВАРИАНТ № 30

Построить эпюры поперечных сил (Q) и изгибающих моментов (М), подобрать сечение стального двутавра и определить в подобранном сечении максимальное касательное напряжение. Принять [ σ ] = 160 МПа.

Дано:

F = 60 кН; q = 30кН/м; m = 10 кН м; a = 2,0 м; b = 4,0 м ; c = 2,0 м; d = 2,0 м.

q F

m

a b c d

Определить: Q, M.

Решение.

1. Отбросив опоры, заменим их действие на балку соответствующими реакциями V_A, V_B. Составляем уравнения равновесия параллельной системы сил, из которых определяем опорные реакции балки:

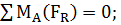……. (1)

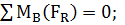…….. (2)

Из уравнения (1) находим V_B:

….

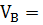Из уравнения (2) находим V_A:

….

Проверяем правильность определения опорных реакций, составляя сумму проекций всех сил на ось Y:

….

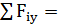т.е. реакции определены верно.

2. Строим расчетную схему и обозначаем на ней характерные точки, по которым будем строить эпюры поперечных сил и изгибающих моментов (рис. а). Под расчетной схемой оставляем место для построения эпюр.

V_A q V_B F

m

рис.а 1 A 2 3 4 5 B 6

2 4 2 2

рис.б Эпюра Q

(кН)

рис.в Эпюра М

(МПа)

Определяем значения поперечной силы Q в характерных сечениях балки, которые обозначены 1, А, 5, В, 6 (рис. а).

=

=

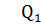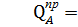
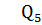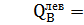
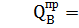
По найденным значениям строим эпюру поперечных сил Q (рис. б).

Для построения эпюры на участке b достаточно было определить поперечную силу в точках А и 5, так как эпюра на этом участке описывается прямой линией.

Так как эпюра пересекает нулевую линию в т.С, необходимо определить абсциссу сечения (расстояние z_o). Для этого ординату в начале распределенной нагрузки (Q_A) делим на интенсивность распределенной нагрузки:

3. Определяем значения изгибающих моментов М в характерных сечениях балки:

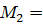
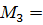
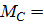
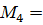
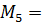
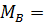
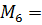
По найденным значениям строим эпюру изгибающих моментов М (рис. в). Строим эпюру на растянутом волокне и знаки на эпюре не ставятся.

4. По эпюре изгибающих моментов определяем положение опасного сечения балки (сечения, в котором изгибающий момент имеет наибольшее по абсолютной величине значение). В нашем случае – это сечение ….., где М_…..= М _max = ……

Из условия прочности балки на изгиб

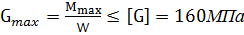
вычисляем необходимый осевой момент сопротивления:

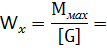
В соответствии с ГОСТ 8239-89 (приложение 1), принимаем сечение из стального двутавра №…… с W = ……

Поверяем:

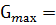
Прочность обеспечена.

5.Проверяем прочность балки по касательным напряжениям. Касательное напряжение вычисляем по формуле Д.И.Журавского

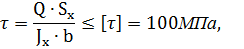
где Q = ….. - максимальное значение Q на эпюре;

S_x= ….. см₃= мм³;

𝐽_x= ….. см⁴= мм⁴;

b=d= …. мм.

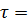
Прочность обеспечена.

Ответ: сечение балки двутавр №….. .

Приложения.

Приложение 1

Приложение 2

МИНИСТЕРСТВО ОБРАЗОВАНИЯ САРАТОВСКОЙ ОБЛАСТИ

государственное автономное профессиональное образовательное учреждение

Саратовской области

«Саратовский архитектурно-строительный колледж»

Специальность 08.02.07

Монтаж и эксплуатация внутренних

сантехнических устройств, кондиционирования

воздуха и вентиляции базовая подготовка

Техническая механика

РАСЧЕТНО-ГРАФИЧЕСКАЯ

РАБОТА № 1

Вариант № Схема №

Разработал студент гр.______ Принял преподаватель

__________________________ Митрякова Н.Б.

Подпись___________________ Подпись________________

Дата______________________ Дата___________________

Саратов 20 г

Приложение 3