Примеры решения систем линейных алгебраических уравнений матричным методом
Рассмотрим матричный метод на примерах. В некоторых примерах мы не будем подробно описывать процесс вычисления определителей матриц, при необходимости обращайтесь к статье вычисление определителя матрицы.
Пример.
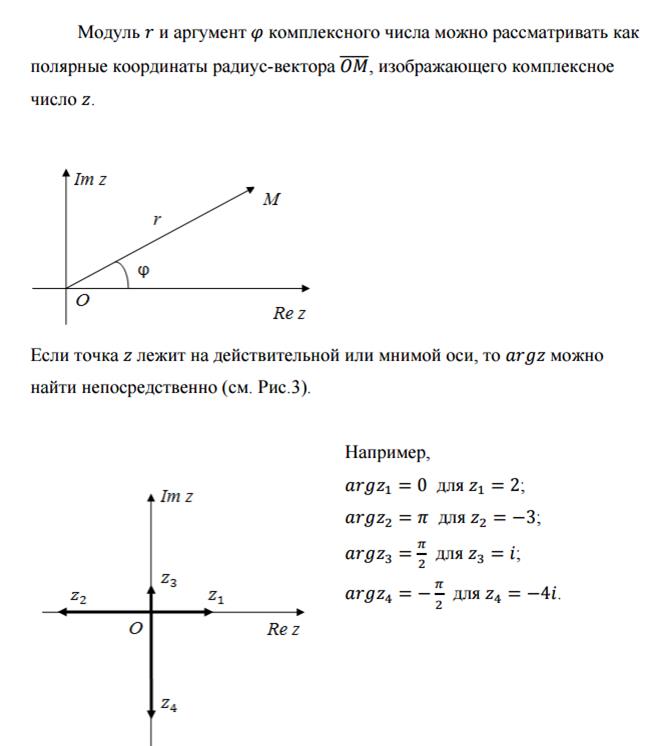
С помощью обратной матрицы найдите решение системы линейных уравнений 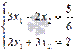 .
.
Решение.
В матричной форме исходная система запишется как 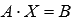 , где
, где  . Вычислим определитель основной матрицы и убедимся, что он отличен от нуля. В противном случае мы не сможем решить систему матричным методом. Имеем
. Вычислим определитель основной матрицы и убедимся, что он отличен от нуля. В противном случае мы не сможем решить систему матричным методом. Имеем 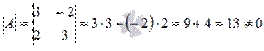 , следовательно, для матрицы А может быть найдена обратная матрица
, следовательно, для матрицы А может быть найдена обратная матрица 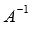 . Таким образом, если мы отыщем обратную матрицу, то искомое решение СЛАУ определим как
. Таким образом, если мы отыщем обратную матрицу, то искомое решение СЛАУ определим как 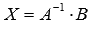 . Итак, задача свелась к построению обратной матрицы
. Итак, задача свелась к построению обратной матрицы 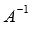 . Найдем ее.
. Найдем ее.
Мы знаем, что для матрицы 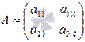 обратная матрица может быть найдена как
обратная матрица может быть найдена как 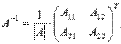 , где
, где 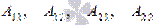 - алгебраические дополнения элементов
- алгебраические дополнения элементов 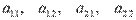 .
.
В нашем случае
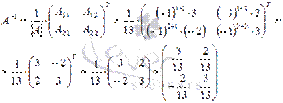
Тогда
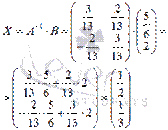
Выполним проверку полученного решения 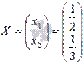 , подставив его в матричную форму исходной системы уравнений
, подставив его в матричную форму исходной системы уравнений 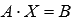 . Это равенство должно обратиться в тождество, в противном случае где-то была допущена ошибка.
. Это равенство должно обратиться в тождество, в противном случае где-то была допущена ошибка.

Следовательно, решение найдено верно. 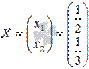 или в другой записи
или в другой записи 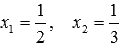 .
.
27. Группы. Свойства групп. Критерий подгруппы
Алгебра G = 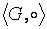 с бинарной операцией
с бинарной операцией 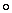 называется группой, если:
называется группой, если:
1) бинарная операция 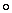 ассоциативна;
ассоциативна;
2) во множестве 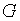 существует элемент
существует элемент 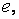 нейтральный относительно операции
нейтральный относительно операции 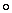 ;
;
3) для любого элемента 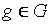 в множестве
в множестве 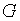 существует элемент
существует элемент 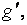 симметричный относительно операции
симметричный относительно операции 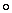 .
.
Существуют различные классификации групп. Наиболее распространёнными являются следующие.
1. В зависимости от того, является ли основное множество 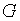 конечным или бесконечным, выделяют соответственно конечные и бесконечные группы.
конечным или бесконечным, выделяют соответственно конечные и бесконечные группы.
2. В зависимости от того, обладает ли бинарная операция 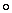 свойством коммутативности или нет, выделяют соответственно коммутативные (абелевы) и некоммутативные (неабелевы) группы.
свойством коммутативности или нет, выделяют соответственно коммутативные (абелевы) и некоммутативные (неабелевы) группы.
3. По виду бинарной операции 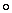 выделяют аддитивные (операция сложения) и мультипликативные (операция умножения) группы.
выделяют аддитивные (операция сложения) и мультипликативные (операция умножения) группы.
Примеры.
1. Алгебра Z = 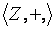 является аддитивной абелевой группой. Действительно, операция сложения целых чисел ассоциативна; нейтральным относительно сложения целых чисел является целое число ноль; для каждого целого числа существует ему симметричное относительно сложения – противоположное по знаку целое число; кроме того, сложение целых чисел коммутативно.
является аддитивной абелевой группой. Действительно, операция сложения целых чисел ассоциативна; нейтральным относительно сложения целых чисел является целое число ноль; для каждого целого числа существует ему симметричное относительно сложения – противоположное по знаку целое число; кроме того, сложение целых чисел коммутативно.
. Пусть a — элемент группы G. Для произвольного целого числа n положим a n = 1, если n = 0, a . . . a, если n > 0 (n множителей), (a −n ) −1 , если n < 0. Предложение 2.1. Пусть a — элемент некоторой группы и n, m ∈ Z. Тогда a n+m = a na m и (a n ) m = a nm. Определение 2.3. Непустое подмножество H группы G называется подгруппой группы G (пишут H ≤ G), если H является 9 группой относительно той же операции, которая определена на G.

28. Поле. Поле комплексных чисел. Действия с комплексными числами в тригонометрической форме.
Полем называется непустое множество, для элементов которого определено два действия, называемых сложением и умножением, которые удовлетворяют следующим аксиомам:
1. 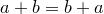 (коммутативность сложения);
(коммутативность сложения);
2. 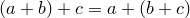 (ассоциативность сложения);
(ассоциативность сложения);
3. 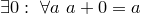 (существование нуля);
(существование нуля);
4. 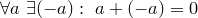 (существование противоположного элемента);
(существование противоположного элемента);
5. 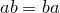 (коммутативность умножения);
(коммутативность умножения);
6. 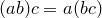 (ассоциативность умножения);
(ассоциативность умножения);
7. 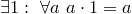 (существование единицы);
(существование единицы);
8. 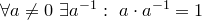 (существование обратного элемента);
(существование обратного элемента);
9. 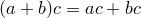 (дистрибутивность);
(дистрибутивность);
10. 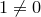 (в поле должно существовать хотя бы два элемента).
(в поле должно существовать хотя бы два элемента).
Пример. Поля: 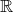 – поле вещественных чисел,
– поле вещественных чисел,  – поле рациональных чисел,
– поле рациональных чисел,
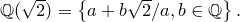
Полем комплексных чисел называется множество 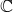 , обладающее следующими свойствами:
, обладающее следующими свойствами:
1. 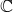 — поле;
— поле;
2. 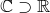 (
( 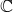 содержит
содержит 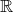 ). При этом предполагается, что действия в
). При этом предполагается, что действия в 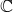 в применении к элементам из
в применении к элементам из 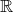 приводят к тем же результатам, что и действия в
приводят к тем же результатам, что и действия в 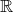 .
.
3. Любое квадратное уравнение с вещественными коэффициентами имеет в поле 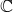 корень.
корень.
4. Каждый элемент поля 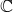 является корнем какого-либо квадратного уравнения с вещественными коэффициентами.
является корнем какого-либо квадратного уравнения с вещественными коэффициентами.
Рассмотрим уравнение
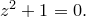
Оно не имеет вещественных корней, но, по аксиоме 3, имеет корень в поле 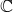 . Один из корней этого уравнения зафиксируем и обозначим
. Один из корней этого уравнения зафиксируем и обозначим 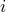 (image) — мнимая единица.
(image) — мнимая единица.
Пусть 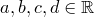
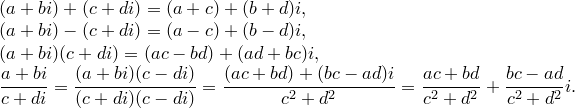
Теорема. Любой элемент поля 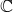 можно единственным образом представить в виде
можно единственным образом представить в виде 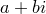 , где
, где 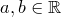 .
.
Доказательство.
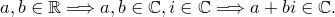
Пусть 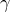 — произвольный элемент
— произвольный элемент 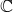 . По аксиоме 4,
. По аксиоме 4, 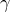 — корень квадратного уравнения с коэффициентами из
— корень квадратного уравнения с коэффициентами из 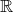

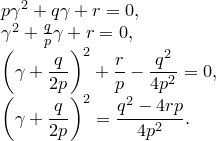
Если 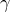 — вещественное число, то его можно представить в виде
— вещественное число, то его можно представить в виде 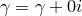 . Пусть
. Пусть 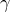 не является вещественным числом. Тогда квадратное уравнение
не является вещественным числом. Тогда квадратное уравнение 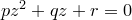 не имеет вещественных корней и имеет отрицательный дискриминант.
не имеет вещественных корней и имеет отрицательный дискриминант.
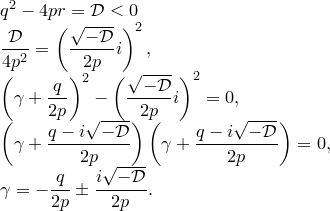
В любом случае 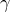 имеет требуемый вид.
имеет требуемый вид.
Докажем единственность.
Предположим, что 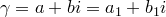 . Тогда
. Тогда
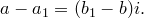
Пусть 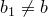 . Тогда
. Тогда
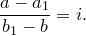
Получаем, что 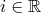 . Это невозможно, значит,
. Это невозможно, значит, 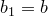 . Тогда
. Тогда 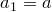 .
.