Описание алгоритма нахождения НОД делением
- Большее число делим на меньшее.
- Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
- Если есть остаток, то большее число заменяем на остаток от деления.
- Переходим к пункту 1.
Пример:
Найти НОД для 30 и 18.
30/18 = 1 (остаток 12)
18/12 = 1 (остаток 6)
12/6 = 2 (остаток 0). Конец: НОД – это делитель. НОД (30, 18) = 6
26. Теорема Кронекера - Капелли. Матричный способ решения систем линейных алгебраических уравнений.
Система линейных уравнений имеет вид:
a11 x1 + a12 x2 +... + a1n xn = b1,
a21 x1 + a22 x2 +... + a2n xn = b2, (5.1)
... ... ... ...
am1 x1 + am1 x2 +... + amn xn = bm.
Здесь аi j и bi (i = 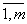 ; j =
; j = 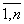 ) - заданные, а xj - неизвестные действительные числа. Используя понятие произведения матриц, можно переписать систему (5.1) в виде:
) - заданные, а xj - неизвестные действительные числа. Используя понятие произведения матриц, можно переписать систему (5.1) в виде:
AX = B, (5.2)
где A = (аi j) - матрица, состоящая из коэффициентов при неизвестных системы (5.1), которая называется матрицей системы, X = (x1, x2,..., xn)T,
B = (b1, b2,..., bm)T - векторы-столбцы, составленные соответственно из неизвестных xj и из свободных членов bi.
Упорядоченная совокупность n вещественных чисел (c1, c2,..., cn) называется решением системы (5.1), если в результате подстановки этих чисел вместо соответствующих переменных x1, x2,..., xn каждое уравнение системы обратится в арифметическое тождество; другими словами, если существует вектор C= (c1, c2,..., cn)T такой, что AC = B.
Система (5.1) называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, илинеразрешимой, если она не имеет решений.
Матрица
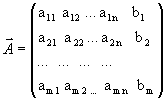 ,
,
образованная путем приписывания справа к матрице A столбца свободных членов, называется расширенной матрицей системы.
Вопрос о совместности системы (5.1) решается следующей теоремой.
Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранги матриц A и 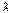 совпадают, т.е.
совпадают, т.е.
r(A) = r(  ) = r.
) = r.
Для множества М решений системы (5.1) имеются три возможности:
1) M = ∅ (в этом случае система несовместна);
2) M состоит из одного элемента, т.е. система имеет единственное решение (в этом случае система называется определенной);
3) M состоит более чем из одного элемента (тогда система называетсянеопределенной). В третьем случае система (5.1) имеет бесчисленное множество решений.
Система имеет единственное решение только в том случае, когда
r(A) = n. При этом число уравнений - не меньше числа неизвестных (m ≥ n); если m>n, то m-n уравнений являются следствиями остальных. Если 0<r<n, то система является неопределенной.
Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, - так называемые системы крамеровского типа:
a11 x1 + a12 x2 +... + a1n xn = b1,
a21 x1 + a22 x2 +... + a2n xn = b2, (5.3)
... ... ... ... ... ...
an1 x1 + an1 x2 +... + ann xn = bn.
Системы (5.3) решаются одним из следующих способов:
1. методом Гаусса, или методом исключения неизвестных;
2. по формулам Крамера;
3. матричным методом.
Пример 2.12. Исследовать систему уравнений и решить ее, если она совместна:
5x1 - x2 + 2x3 + x4 = 7,
2x1 + x2 + 4x3 - 2x4 = 1,
x1 - 3x2 - 6x3 + 5x4 = 0.
Решение. Выписываем расширенную матрицу системы:
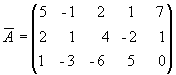 .
.
Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу 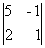 = 7 ≠ 0; содержащие его миноры третьего порядка равны нулю:
= 7 ≠ 0; содержащие его миноры третьего порядка равны нулю:
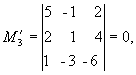
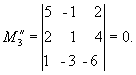
Следовательно, ранг основной матрицы системы равен 2, т.е. r(A) = 2. Для вычисления ранга расширенной матрицы 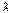 рассмотрим окаймляющий минор
рассмотрим окаймляющий минор
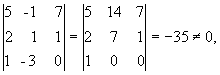
значит, ранг расширенной матрицы r( 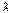 ) = 3. Поскольку r(A)≠ r(
) = 3. Поскольку r(A)≠ r( 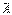 ), то система несовместна.
), то система несовместна.
В этой статье поговорим о матричном методе решения систем линейных алгебраических уравнений вида 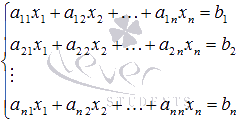 , которые в матричной форме записываются как
, которые в матричной форме записываются как 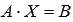 , где
, где 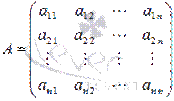 - основная матрица системы,
- основная матрица системы, 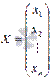 - матрица-столбец неизвестных переменных,
- матрица-столбец неизвестных переменных,  - матрица свободных членов.
- матрица свободных членов.
Сначала опишем суть матричного метода, остановимся на условии применимости этого метода, далее подробно разберем решения нескольких примеров.
Сразу оговоримся, что решение систем линейных алгебраических уравнений матричным методом и решение СЛАУ с помощью обратной матрицы есть одно и то же. Поэтому рекомендуем освежить в памяти теорию раздела обратная матрица: определение, свойства, методы нахождения.
Приступим.Матричный метод решения систем линейных алгебраических уравнений - вывод формулы.
Пусть для матрицы А порядка n на n существует обратная матрица 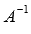 . Умножим обе части матричного уравнения
. Умножим обе части матричного уравнения 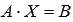 слева на
слева на 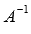 (порядки матриц A ⋅ X и Впозволяют произвести такую операцию, смотрите статью операции над матрицами, свойства операций). Имеем
(порядки матриц A ⋅ X и Впозволяют произвести такую операцию, смотрите статью операции над матрицами, свойства операций). Имеем 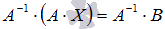 . Так как для операции умножения матриц подходящих порядков характерно свойство ассоциативности, то последнее равенство можно переписать как
. Так как для операции умножения матриц подходящих порядков характерно свойство ассоциативности, то последнее равенство можно переписать как 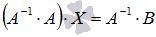 , а по определению обратной матрицы
, а по определению обратной матрицы 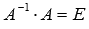 (E – единичная матрица порядка n на n), поэтому
(E – единичная матрица порядка n на n), поэтому
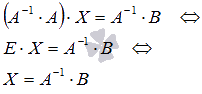
Таким образом, решение системы линейных алгебраических уравнений матричным методом определяется по формуле 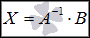 . Другими словами, решение СЛАУ находится с помощью обратной матрицы
. Другими словами, решение СЛАУ находится с помощью обратной матрицы 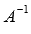 .
.
Мы знаем, что квадратная матрица А порядка n на n имеет обратную матрицу 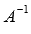 только тогда, когда ее определитель не равен нулю. Следовательно, СИСТЕМУ nЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ.
только тогда, когда ее определитель не равен нулю. Следовательно, СИСТЕМУ nЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ.
