Мощность множества, счетные множества и их свойства. Счетность множества рациональных чисел. Несчетность множества действительных чисел
Под множеством понимают объединение в одно целое объектов, связанных между собой неким свойством. Если из элементов двух множеств можно составить пары таким образом, чтобы каждому элементу первого множества соответствовал определенный элемент второго множества, а каждому элементу второго множества соответствовал один и только один элемент первого множества, то говорят, что между такими двумя множествами установлено взаимно однозначное соответствие.
Чтобы установить взаимно однозначное соответствие, необязательно пересчитывать элементы множеств. Например, мы знаем, что американские штаты находятся во взаимно однозначном соответствии с их столицами, хотя можем оставаться в неведении относительно общего их числа. Мы могли бы утверждать: «Столиц штатов ровно столько, сколько штатов».
Конечное множество состоит из конечного числа элементов, например, множество страниц в книге, множество студентов в группе и т.д.
Бесконечное множество состоит из бесконечного числа элементов, т.е. это множество, которое не является ни конечным, ни пустым. Например: множество действительных чисел, множество точек плоскости, множество атомов во Вселенной и т.д.
Мощностью конечного множества называется количество его элементов. Мощность множества A обозначается m (A).
В теории множеств, счётное мно́жество есть бесконечное множество, элементы которого возможно пронумеровать натуральными числами. Более формально: множество {\displaystyle X}  является счётным, если существует биекция {\displaystyle X\leftrightarrow \mathbb {N} }
является счётным, если существует биекция {\displaystyle X\leftrightarrow \mathbb {N} }  , где {\displaystyle {\mathbb {N} }}
, где {\displaystyle {\mathbb {N} }}  обозначает множество всех натуральных чисел. Другими словами, счётное множество — это множество, равномощное множеству натуральных чисел.
обозначает множество всех натуральных чисел. Другими словами, счётное множество — это множество, равномощное множеству натуральных чисел.
1. Любое подмножество счётного множества не более чем счётно (т.е. конечно или счётно).[1]
2. Объединение конечного или счётного числа счётных множеств счётно.[1]
3. Прямое произведение конечного числа счётных множеств счётно.
4. Множество всех конечных подмножеств счётного множества счётно.
5. Множество всех подмножеств счётного множества континуально и, в частности, не является счётным.
2.2 Свойства счётных множеств
Лемма 1. Объединение двух счётных множеств счётно.
Доказательство. Рассмотрим два счетных множества A и B; каждое из них можно записать в последовательность: a0, a1, a2, a3, . . . b0, b1, b2, b3, . . . Теперь нетрудно перечислить и элементы множества A ∪ B, чередуя элементы из A с элемен- тами из B: a0, b0, a1, b1, a2, b2, . . . . Если A и B не пересекаются, то на этом рассуждение заканчивается — но если пересекаются, то в этой последовательности общие элементы встретятся по два раза. Как это исправить? Если очередной элемент уже встречался ранее (например, если элемент aj совпадает с элементом bi , где i < j), то мы его пропускаем и второй раз не выписываем
. Лемма 2. Всякое подмножество счетного множества конечно или счетно.
Доказательство. Рассмотрим счётное множество A и его подмножество A0 . Выпишем элемен- ты A в последовательность a0, a1, a2, a3, . . . . Вычеркнем из этой последовательности те элементы, которые не лежат в A0 . В результате останется последовательность элементов A0 — конечная или бесконечная. В первом случае множество будет конечным, во втором счётным. Формально говоря, для бесконечного подмно- жества A0 ⊂ A искомая биекция f : N → A0 ставит в соответствие числу n элемент множества A0 , который стоит n-м по счёту в последовательности (если считать только элементы A0 ).
Лемма 3. Всякое бесконечное множество содержит счётное подмножество.
Доказательство. Рассмотрим прозвольное бесконечное множество A. Нам надо выписать по- следовательность из некоторых его элементов, не обязательно всех. Будем действовать самым простым образом. Первый элемент a0 возьмем произвольно. Поскольку A бесконечно, в нем есть ещё элементы (кроме a0). В качестве a1 возьмем любой из них. И так далее. В общем случае, когда нам нужно выбрать очередной элемент an, мы рассматриваем подмножество {a0, . . . , an−1}. Оно конечно, а значит, не совпадает со всем множеством A (которое по пред- положению бесконечно). Значит, в A есть элементы, не лежащие в этом подмножестве — и мы можем взять любой из них в качестве an. Получили бесконечную последовательность из элементов A, и множество элементов этой последовательности образует искомое счётное подмножество множества A. Две последние леммы объясняют, в каком смысле счётные множества — это «самые малень- кие» бесконечные множества. Между ними и конечными нет ничего промежуточного (лемма 2), и всякое бесконечное множество «не меньше» счётного в том смысле, что в нём есть счётное подмножество (лемма 3). Позже мы увидим, что бывают и б´ольшие (несчётные) бесконечные множества. Например, таким оказывается множество действительных чисел (или точек на прямой), но и это не предел. Пока же продолжим изучение счётных множеств.
Лемма 4. Множество рациональных чисел Q счетно.
Доказательство. Нам будет удобнее доказать отдельно, что множество неотрицательных ра- циональных чисел счётно и что множество отрицательных рациональных чисел счётно. Тогда счётность множества всех рациональных чисел сразу вытекает из леммы 1. Проведем рассуждение для неотрицательных рациональных чисел. Для отрицательных чи- сел рассуждение аналогично (а можно заметить, что смена знака даёт биекцию между отрица- тельными и положительными числами, а к положительным рациональным числам применить лемму 2). 5 Неотрицательное рациональное число задается парой чисел — числителем и знаменателем. Числитель может быть произвольным натуральным числом, а знаменатель произвольным положительным натуральным числом.
Выпишем все такие числа в виде таблицы, бесконечной вниз и вправо:
0/1 1/1 2/1 3/1 . . .
0/2 1/2 2/2 3/2 . . .
0/3 1/3 2/3 3/3 . . .
0/4 1/4 2/4 3/4 . . . . . . . . . . . . . . . . . . .
В строке с номером i этой таблицы стоят последовательно все числа со знаменателем i, а в столбце с номером j — все числа с числителем j. В этой таблице будут выписаны все рациональ- ные числа, причем некоторые будут повторяться много раз (например, 0/1 = 0/2 = 0/3 = . . . и 1/2 = 2/4 = 3/6 = . . .). Числа из этой таблицы теперь уже легко выписать в последовательность. Например, можно идти по диагоналям (вниз-влево). Сначала выпишем единственное число на первой диагонали (0/1), потом два числа на второй (1/1, 0/2), потом три числа на третьей и так далее: 0/1, 1/1, 0/2, 2/1, 1/2, 0/3, 3/1, 2/2, 1/3, 0/4, . . . . Другими словами, мы сначала выписываем все числа с суммой числителя и знаменателя 1, потом — с суммой 2, потом 3 и так далее. Конечно, нужно не забыть выбрасывать из последо- вательности повторяющиеся члены. То есть, когда мы доходим в таблице до очередного числа и видим что равное ему уже было выписано, мы пропускаем текущее число и переходим к следующему. Получится такая последовательность рациональных чисел: 0, 1, 2, 1/2, 3, 1/3, . . . . В этом доказательстве на самом деле не имеет значения, что именно мы записываем в бесконечную вправо и вниз таблицу: верно такое общее утверждение.
Теорема 1. Объединение конечного или счётного числа конечных или счётных множеств конечно или счётно.
Доказательство. Пусть есть счётное количество счётных множеств A0, A1, A2, . . .. Как и в прошлой лемме, расположим их элементы в виде таблицы:
A0 : a00 a01 a02 a03 . . .
A1 : a10 a11 a12 a13 . . .
A2 : a20 a21 a22 a23 . . .
A3 : a30 a31 a32 a33 . . . . . . . . . . . . . . . . . . . . . . Здесь в первой строке мы последовательно выписали элементы A0, во второй — элементы A1 и так далее. Теперь снова соединяем эти последовательности в одну, идя по диагоналям: a00, a01, a10, a02, a11, a20, a03, a12, a21, a30, . . . . При этом нужно следить, чтобы члены последовательности не повторялись: когда мы рассматриваем очередной элемент таблицы, нужно проверить, не встретился ли он раньше. Если он уже был, его нужно пропустить. Мы предполагали, что все Ai счётны и что их счётное число. Если самих множеств лишь конечное число, или если какие-то из множеств конечны, то в таблице часть ячеек окажется пустой. Соответственно, мы будем их пропускать при составлении последовательности. В результате либо получится бесконечная последовательность, и тогда объединение счётно, либо получится только конечная последовательность — и тогда объединение конечно. 6 По существу ту же теорему можно сформулировать иначе:
Теорема 2. Декартово произведение двух счётных множеств A × B cчётно.
Доказательство. В самом деле, по определению декартово произведение есть множество всех упорядоченных пар вида ha, bi, в которых a ∈ A и b ∈ B. Разделим пары на группы, объединив пары с одинаковой первой компонентой (каждая группа имеет вид {a}×B для какого-то a ∈ A). Тогда каждая группа счётна, поскольку находится во взаимно однозначном соответствии с B (пара определяется своим вторым элементом), и групп столько же, сколько элементов в A, то есть счётное число.
Теорема 1. Множество всех рациональных чисел счетно.
Доказательство. Рассмотрим сначала положительные рациональные числа 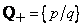 . Назовем натуральное число
. Назовем натуральное число 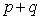 высотой рационального числа
высотой рационального числа 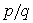 . Пусть
. Пусть  - множество всех рациональных чисел с высотой, равной
- множество всех рациональных чисел с высотой, равной 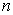 . Множества
. Множества 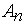 состоят из конечного числа элементов (рациональных чисел), например
состоят из конечного числа элементов (рациональных чисел), например
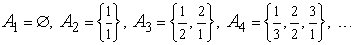 .
.
Легко видеть, что  ,
,
Перенумеруем числа, записанные в фигурных скобках слева направо, выпуская, впрочем, на каждом этапе нумерации те, которые были уже занумерованы на более раннем этапе. В результате получим последовательность
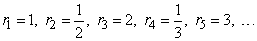 .
.
Так как рациональных положительных чисел бесконечно много, то мы используем все натуральные числа. Значит, 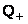 счетно. Далее, очевидно, что
счетно. Далее, очевидно, что 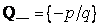 счетно. Поэтому все множество рациональных чисел
счетно. Поэтому все множество рациональных чисел 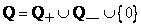 также счетно.
также счетно.
Теорема 2.Множество всех действительных чисел несчетно.
Доказательство. Для доказательства достаточно установить, что множество действительных чисел интервала 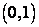 образует несчетное множество. Допустим противное, что интервал
образует несчетное множество. Допустим противное, что интервал 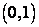 есть счетное множество, т. е. все его точки можно перенумеровать:
есть счетное множество, т. е. все его точки можно перенумеровать:
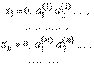
Но это предположение противоречиво. В самом деле, построим вещественное число 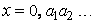 , где цифры
, где цифры 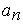 подобраны так, чтобы
подобраны так, чтобы 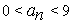 и
и 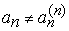 . Ясно, что
. Ясно, что 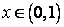 , однако
, однако 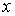 не совпадает ни с одним из чисел
не совпадает ни с одним из чисел 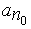 , так как иначе должно было бы быть
, так как иначе должно было бы быть 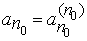 , что не имеет места.
, что не имеет места.
