Последовательность расчета
4.1.4.1. Источник ЭДС Е2 заменяется его внутренним сопротивлением (в рассматриваемой задаче приняты идеальные источники ЭДС, т.е. их внутренние сопротивления равны нулю).
Схема для определения частичного тока, создаваемого источником ЭДС Е1 дана на рис. 8.
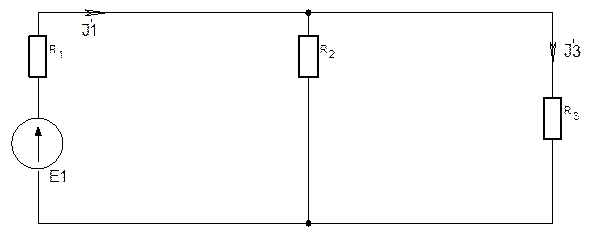
Рис. 8. Схема для расчета частичного токаI3.
4.1.4.2. Находится частичный ток I3 с использованием правил определения эквивалентных сопротивлений при параллельном и последовательном соединении пассивных элементов и закон Ома.
а) Эквивалентное сопротивление R23 параллельно включенных сопротивлений R2 и R3
R23 = R2 R3/ (R2+R3)(4.1.16)
полное сопротивление цепиRц.
Rц. = R1 + R23(4.1.17)
б) Ток I1 в неразветвленной части цепи
I1 = Е1/ Rц.(4.1.18)
в) Напряжение на сопротивлении R3
U3 = U23 = I1 R23(4.1.19)
г) Частичный ток 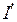 3
3
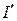 3 = U3/ R3(4.1.20)
3 = U3/ R3(4.1.20)
3) Для определения частичного тока 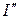 3 расчет следует повторить, оставив в цепи только источник ЭДС Е2.
3 расчет следует повторить, оставив в цепи только источник ЭДС Е2.
4) Действительный ток I3
I3 = 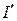 3 +
3 + 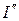 3(4.1.21)
3(4.1.21)
После выполнения расчетов каждым методом необходимо сравнить значения тока I3.
Задача 2
4.2.1. При составлении расчетной схемы учитываются ее параметры, указанные в задании, т.е. на схеме показываются только те источники питания, которые предусмотрены таблицей вариантов: источники ЭДС заменяются перемычками, если
Е = 0, а источники тока разрывом, если J= 0.
При расчете схемы внутренние сопротивления источников ЭДС принять равными нулю, т.е. полагать источники идеальными. Источники тока J и включенные параллельно с ними сопротивления rпар. следует заменить эквивалентными источниками ЭДС E с внутренними сопротивлениями rвн., используя формулы эквивалентного преобразования
E = Jrпар.(4.2.1)
rвн. = rпар.(4.2.2)
Схема участка цепи с источником тока до преобразования дана на рисунке 9а; на рисунке 9б показан эквивалентный участок с источником ЭДС.

а) б)
Рис. 9. Схема участка цепи до (а) и после (б) преобразования источника тока
в источник ЭДС.
4.2.2. Порядок выполнения задания рассмотрен на примере расчета электрической цепи, схема которой дана на рисунке 10.
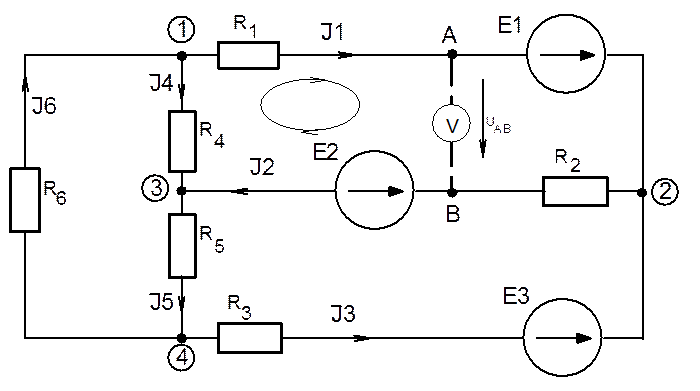
Рис. 10. Схема замещения к задаче № 2
Параметры элементов цепи имеют следующие значения: Е1 = 30 В; Е2 = 16 В;
Е3 = 10 В; R1 = 2 Ом; R2 = 5 Ом; R3 = 3 Ом; R4 = 1 Ом; R5 = 8 Ом; R6 = 5 Ом.
Решение.
4.2.2.1 Расчет цепи методом контурных токов.
1) Определяются контуры, для которых можно составить уравнения контурных токов, и произвольно принимаются направления этих токов. Расчетная схема для расчета методом контурных токов дана на рисунке 11.
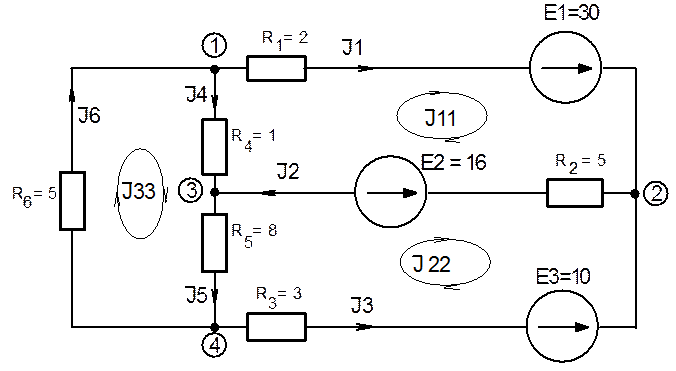
Рис. 11. Расчетная схема для расчета цепи методом контурных токов.
2) Уравнения контурных токов для этой схемы имеют вид:
I11 R11 - I22 R12 - I33 R13 = Е11;
- I11 R21 + I22 R22 - I33 R23 = Е22;(4.2.3)
- I11 R31 - I22 R32 - I33 R33 = Е33,
где R11 = R1 + R2 + R4 = 2 + 5 + 1 = 8 Ом; R22 = R2 + R3 + R5 = 5 + 3 + 8 = 16 Ом;
R33 = R4 + R5 + R6 = 1 + 8 + 5 = 14 Ом;
R12 = R21 = R2 =5 Ом; R23 = R32 = R5 =8 Ом; R13 = R31 = R4 =1 Ом;
Е11 = Е1 – Е2 = 30 - 16 = 14 В; Е22 = Е2 – Е3 = 16 - 10 = 6 В; Е33 = 0.
Система уравнений после подстановки числовых значений
8I11 - 5I22 - I33 = 14;
- 5I11 + 16I22 - 8I33 = 6;(4.2.4)
- I11 - 8I22 + 14I33 = 0.
3) Составляются определители контурных уравнений: основной  и дополнительные
и дополнительные  1,
1,  2,
2,  3 .
3 .
 8 -5 -1
8 -5 -1 
 14 -5 -1
14 -5 -1 
 =
= 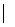 -5 16 -8
-5 16 -8  = 834;
= 834;  1 =
1 =  6 16 -8
6 16 -8  = 2708;
= 2708;
 -1 -8 14
-1 -8 14 
 0 -8 14
0 -8 14 
 8 14 -1
8 14 -1 
 8 -5 14
8 -5 14 
 2 =
2 =  -5 6 -8
-5 6 -8  = 1758;
= 1758;  3 =
3 =  -5 16 6
-5 16 6 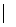 = 1198.
= 1198.
 -1 0 14
-1 0 14 
 -1 -8 0
-1 -8 0 
4) По найденным определителям вычисляются контурные токи:
I11 =  1 /
1 /  = 2708/834 = 3,247 А;I22 =
= 2708/834 = 3,247 А;I22 =  2 /
2 /  = 1758/834 = 2,108 А;
= 1758/834 = 2,108 А;
I33 =  3 /
3 /  = 1198/834 = 1,436 А.
= 1198/834 = 1,436 А.
5) По контурным токам определяются токи в ветвях цепи:
I1 = I11 = 3,247 А; I2 = I11 - I22 = 3,247 – 2,108 = 1,139 А;
I3 = - I22 = - 2,108 А; I4 = I33 – I11 = 1,436 – 3,247 = -1,811 А;
I5 = I33 – I22 = 1,436 – 2,108 = - 0,672 А; I6 = I33 = 1,436 А.
4.2.2.2 Составление системы уравнений Кирхгофа.
1) На схеме (рис. 11) указываются направления токов I 1, I2, I3, I4 , I5, I6 в ветвях с учетом их знаков и направлений контурных токов и составляются узловые уравнения по первому закону Кирхгофа для независимых узлов 1, 2, и 3.
2) Число независимых уравнений на единицу меньше общего числа узлов в цепи.
I6 – I1 – I4 = 0;
I1 + I3 - I2 = 0;(4.2.5)
I4 + I2 – I5 = 0.
3) Выбираются независимые контуры и произвольно принимаются направления их обхода; для всех контуров по второму закону Кирхгофа составляются контурные уравнения.
I6 R1 + I2 R2 – I4 R4 = E1 – E2;
-I2 R2 – I3 R3 – I5 R5 = E2 – E3;(4.2.6)
I4 R4 + I5 R5 + I6 R6 = 0.
4) Проводится правильность расчетов подстановкой найденных значений токов в уравнения, составленные по законам Кирхгофа.
4.2.2.3 Замена соединения сопротивлений треугольником соединением звездой.
Треугольником соединены сопротивления R4; R5; R6.
Сопротивления эквивалентного соединения в звезду имеют значения:
R46 = R4 R6/ (R4 + R5 + R6) = 0,357 Ом;
R45 = R4 R5/( R4 + R5 + R6 ) = 0,571 Ом; (4.2.7)
R56 = R5 R6/(R4 + R5 + R6) = 2,857 Ом;
4.2.2.4 Определение напряжения между точками А и В схемы.
1) Для определения напряжения UАВ составляется уравнение по второму закону Кирхгофа для замкнутого контура, который показан штриховой линией на рис. 11
UАВ - I4 R4 + I1 R1 + Е2 = 0(4.2.8)
2) Из этого уравнения находится UАВ
UАВ = - Е2 - I1 R1 + I4 R4 = -16 - 3,247 2 – 1,811 = -24,305 В.
Действительное направление напряжения между узлами А и В противоположно обозначенному на схеме.
4.2.2.4 Составление баланса мощностей.
При составлении баланса следует учитывать, что мощность, потребляемая всеми элементами цепи, должна быть равна мощности, которую отдают источники электроэнергии. Однако возможно и потребление энергии источником (например, при зарядке аккумулятора). В этом случае направления ЭДС и тока источника противоположны.
1) Мощность источников электроэнергии
Рист. = Е1 I1 + Е2I2 +Е3I3(4.2.9)
или
Рист. = 30 3,247 -16 1,139 – 10 2,108 = 58,1 Вт.
2) Определяется потребляемая сопротивлениями цепи мощность
РR = I1 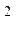 R1 + I
R1 + I 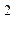 2 R2 + I
2 R2 + I 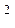 3 R3 + I4
3 R3 + I4 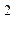 R4 + I5
R4 + I5 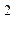 R5 + I6
R5 + I6 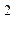 R6(4.2.10)
R6(4.2.10)
После подстановки числовых значений получается РR = 58,1 Вт, т.е. баланс мощностей выполняется, что свидетельствует о правильности вычисления токов в ветвях.
Задача 3
4.3.1. При расчетах цепей переменного синусоидального тока используются те же законы и методы, что и при расчете цепей постоянного тока, но все электрические величины – токи, ЭДС, напряжения, сопротивления, - должны быть записаны в комплексной форме. В связи с необходимостью выполнения при расчетах различных математических действий: сложения/вычитания, умножения/деления,- рекомендуется использовать как алгебраическую, так и показательную формы записи комплексных чисел.
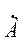 =а + jb =A e
=а + jb =A e 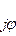 ,(4.3.1)
,(4.3.1)
где А – модуль величины,
а и b – ее действительная и мнимая части.
А = 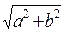 (4.3.2)
(4.3.2)
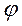 = arc tg b/a (4.3.3)
= arc tg b/a (4.3.3)
для перехода от показательной формы записи к алгебраической нужно использовать выражения
а = А cos 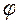 (4.3.4)
(4.3.4)
b = A sin 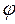 (4.3.5)
(4.3.5)
4.3.2.При составлении расчетной схемы необходимо:
а) заменить полные сопротивления составляющими их элементами: активными сопротивлениями, индуктивностями и емкостями;
б) источники тока источниками ЭДС.
Ветви с источниками тока, равными нулю, на схему не наносятся.
4.3.3. Для определения линейной частоты f следует использовать связывающее ее с угловой частотой 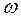 соотношение
соотношение
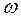 = 2пf(4.3.6)
= 2пf(4.3.6)
4.3.4. Расчет токов в ветвях следует вести в изложенной ниже последовательности
а) Вычислить сопротивления реактивных элементов
ХL = 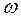 L (Ом)(4.3.7)
L (Ом)(4.3.7)
ХC = 1/ 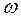 C (Ом)(4.3.8)
C (Ом)(4.3.8)
б) Записать в комплексной форме заданные величины, используя приведенные в п. 4.3.1 формулы.
Например:
- ЭДС дана в виде Е = 100 В; 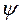 = 650; тогда показательная форма этой ЭДС имеет вид
= 650; тогда показательная форма этой ЭДС имеет вид
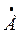 = 100 е j65
= 100 е j65 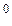 ,
,
а перевод ее в алгебраическую форму выполняется по (4) и (5);
- сопротивление ветви состоит из резистора R, индуктивного ХL и емкостного ХС сопротивлений
R = 3 Ом; ХL = 9 Ом; ХС = 5 Ом. Тогда удобней первоначальную запись комплексного сопротивления выполнить в алгебраической форме
Z = R + j (ХL – ХС) = 3 + j (9 – 5) = 3 + j 4
c последующим ее переводом в показательную форму по (4.3.1) – (4.3.3).
Результаты расчетов занести в таблицу 6.
Таблица 6 - Результаты расчета заданных величин и параметров схемы
в алгебраической и показательной форме.
| Величина, параметр | Алгебраическая форма | Показательная форма |
в) Составить контурные уравнения для своей расчетной схемы замещения, используя выражение ЭДС и сопротивлений комплексными числами. Для упрощения операций умножения и деления при составлении уравнений предпочтительней использовать показательную форму комплексов.
г) Решить полученную систему уравнений и, найдя контурные токи, определить токи в ветвях, напряжения на каждом комплексном сопротивлении и их элементах. Результаты расчетов занести в таблицу 7. Количество строк в таблице зависит от числа найденных величин.
Таблица 7 - Результаты расчета токов и напряжений.
| Искомая величина | Алгебраическая форма | Показательная форма | Действующее значение |
Правильность расчетов может быть проверена по уравнениям, составленным по первому закону Кирхгофа.
4.3.5. Найти комплекс мощности S источника питания как произведение комплекса ЭДС источника на сопряженный комплекс тока 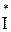 , даваемого этим источником.
, даваемого этим источником.
S = 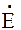
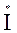 ,(4.3.9) где сопряженный комплекс тока равен комплексу тока, у которого знак мнимой части изменен на противоположный. Например,
,(4.3.9) где сопряженный комплекс тока равен комплексу тока, у которого знак мнимой части изменен на противоположный. Например, 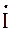 = 3 + j4, тогда сопряженный комплекс в алгебраической форме
= 3 + j4, тогда сопряженный комплекс в алгебраической форме 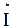 = 3 - j4.
= 3 - j4.
При использовании показательной формы необходимо в сопряженном комплексе изменить знак показателя.
Заменой комплекса тока на его сопряженный комплекс учитывается угол сдвига фаз между ЭДС и током для источников питания (напряжением и током для приемников).
Полная мощность равна модулю комплекса мощности, или
S = Е I,(4.3.10)
а действительная и мнимая части комплекса мощности соответствуют активной и реактивной мощности, или
Р = S cos 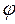 ;(4.3.11)
;(4.3.11)
Q = S sin 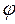 ,(4.3.12)
,(4.3.12)
где 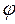 - угол сдвига по фазе между ЭДС и током источника питания.
- угол сдвига по фазе между ЭДС и током источника питания.
Суммарную мощность всех действующих в цепи источников питания проще найти, записав комплексы мощностей каждого источника в алгебраической форме.
Результаты определения мощностей показать в таблице, форму которой составить самостоятельно.
4.3.6. Для составления баланса активных мощностей следует определить активную мощность, потребляемую активными сопротивлениями (резисторами) n-й ветви цепи
Pпотр. = 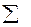 I n
I n  Rn ,(4.3.13)
Rn ,(4.3.13)
где In – действующее значение тока ветви, А;
Rn – активное сопротивление ветви, Ом.
Потребляемая цепью активная мощность должна быть равна активной мощности, отдаваемой всеми источниками питания (см. п. 4.3.5).
4.3.7. Уравнения мгновенных значений заданных ЭДС имеют вид
е = Еm sin ( 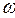 t +
t + 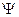 ) (4.3.14)
) (4.3.14)
где 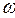 - угловая частота,
- угловая частота, 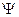 - начальная фаза каждой ЭДС (см. задание).
- начальная фаза каждой ЭДС (см. задание).
4.3.8. Построение векторной диаграммы.
Для данной на рис.12 схемы выполнен расчет, результаты которого отражены в общем виде в таблице 7а, где действительные части комплексов токов 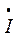 и напряжений
и напряжений 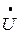 обозначены I' и U' , а мнимые I" и U".
обозначены I' и U' , а мнимые I" и U".
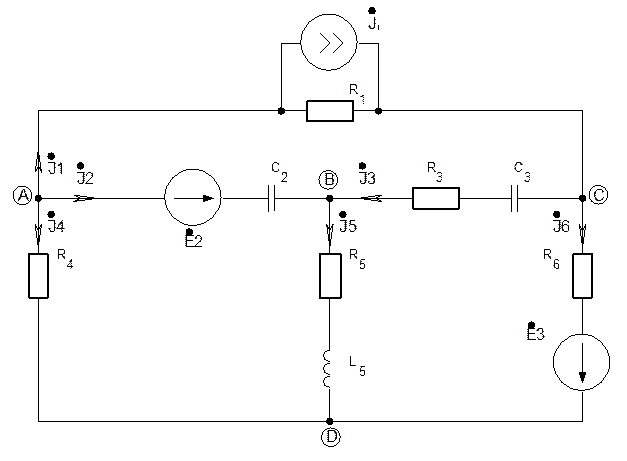
Рис. 12. Схема однофазной цепи
Таблица 7а - Результаты расчета токов и напряжений
| Искомая величина | Алгебраическая форма | Показательная форма | Действующее значение | |
| Токи ветвей, А | 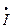 1 1 | I'1 + jI"1 | I1 e 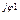 | I1 |
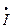 2 2 | I'2 + jI"2 | I2 e 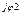 | I2 | |
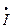 3 3 | I'3 + jI"3 | I3 e 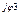 | I3 | |
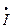 4 4 | I'4 + jI"4 | I4 e 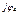 | I4 | |
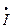 5 5 | I'5 + jI"5 | I5 e 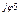 | I5 | |
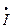 6 6 | I'6 + jI"6 | I6 e 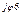 | I6 |
Продолжение таблицы 7а
| Напряжения на сопротивлениях, В | 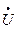 1 = 1 = 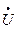 R1 R1 | U'1 + j U"1 | U1 e 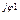 | U1 |
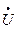 2 = 2 = 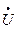 C2 C2 | U'2+ jU"2 | U2 e 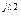 | U2 | |
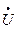 3 3 | U'3 + jU"3 | U3 e 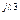 | U3 | |
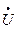 R3 R3 | U'R3 + jU"R3 | UR3 e 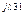 | UR3 | |
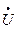 C3 C3 | U'C3 + jU"C3 | UC3 e 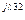 | UC3 | |
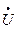 4 = 4 = 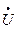 R4 R4 | U'4 + jU"4 | U4 e 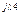 | U4 | |
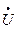 5 5 | U'5 + jU"5 | U5 e 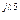 | U5 | |
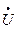 R5 R5 | U'R5 + jU"R5 | UR5 e 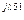 | UR5 | |
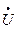 5 5 | U'L5 + jU"L5 | UL5 e 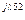 | UL5 | |
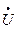 6 = 6 = 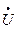 R6 R6 | U'6 + jU"6 | U6 e 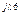 | U6 |
На рис. 13 дана векторная диаграмма токов и напряжений в цепи, при построении которой соблюдалась следующая последовательность:
1. Строятся оси комплексной плоскости: действительных величин (+1) – горизонтально, мнимых величин (j) – вертикально.
2. Исходя из значений модулей токов и напряжений и размеров поля листа, отведенного для построения диаграммы, выбираются масштабы тока mI и напряжения mU. Например, при использовании формата А4 (размеры 210х297 мм) при наибольших модулях тока 40 А и напряжения U = 500 В приняты масштабы: mI = 5 А/см, mU = 50 В/см.
3. С учетом принятых масштабов mI и mU определяется длина каждого вектора, если диаграмма строится с использованием показательной формы его записи; при использовании алгебраической формы находятся длины проекций векторов на оси действительных и мнимых величин, т.е. длины действительной и мнимой частей комплекса.
Например, для записанных в комплексной форме тока, I = 40 е 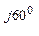 = 20 + j34,6 и напряжения U = 500 е
= 20 + j34,6 и напряжения U = 500 е 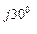 = 433 + j 250 В:
= 433 + j 250 В:
- длина вектора тока /I / = 40 А/ 5 А/см = 8 см; длина его действительной части I = 20 А / 5 А/см = 4 см, длина его мнимой части I = 34,6 А / 5 А/см = 6,9 см;
- длина вектора напряжения / U / = 500 В / 50 В/см = 10 см; длина его действи-
тельной части U = 433 В / 50 В/см = 8,66 см; длина его мнимой части U =
= 250 В / 50 В/см = 5 см.
Результаты определения длин векторов, их действительных и мнимых частей нужно отразить в таблице 7б.
Таблица 7б - Длины векторов тока и напряжения, их действительных и
мнимых частей
| Величина | Масштаб, 1/см | Длина вектора, см | Длина действительной части, см | Длина мнимой части, см | |
| Токи ветвей | 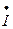 1 1 | mI= 5 А/см | |||
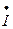 2 2 | |||||
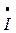 3 3 | |||||
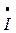 4 4 | |||||
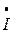 5 5 | |||||
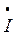 6 6 | |||||
| ЭДС и напряжения | 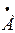 1 1 | mU=50 В/см | |||
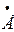 2 2 | |||||
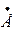 6 6 | |||||
 1= 1=  R1 R1 | |||||
 R1 R1 | |||||
 2 = 2 =  C2 C2 | |||||
 3 3 | |||||
 R3 R3 |
Продолжение таблицы 7б
| ЭДС и напряжения |  C3 C3 | mU=50 В/см | |||
 4 = 4 =  R4 R4 | |||||
 5 5 | |||||
 R5 R5 | |||||
 L5 L5 | |||||
 6 = 6 =  R6 R6 |
4. На комплексной плоскости строятся вектора всех ЭДС, напряжений и токов. Для их построения можно использовать обе формы записи комплексов ЭДС, напряжений и токов.
Например, вектор тока 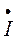 , комплекс которого использован в п. 3 в качестве примера, строится по показательной форме следующим образом: от оси (+1) под углом 30
, комплекс которого использован в п. 3 в качестве примера, строится по показательной форме следующим образом: от оси (+1) под углом 30 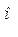 , т.е. против часовой стрелки, откладывается отрезок длиной 8 см; по алгебраической форме его можно построить, отложив по оси (+1) отрезок длиной 4 см, а по оси (j) отрезок длиной 6,96 см, концы этих отрезков являются координатами конца вектора
, т.е. против часовой стрелки, откладывается отрезок длиной 8 см; по алгебраической форме его можно построить, отложив по оси (+1) отрезок длиной 4 см, а по оси (j) отрезок длиной 6,96 см, концы этих отрезков являются координатами конца вектора 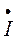 .
.
На векторной диаграмме (рис. 13) использованы оба способа построения векторов: векторы токов построены по показательной форме записи, а векторы ЭДС и напряжений по алгебраической.
5. Правильность расчета цепи и построения векторной диаграммы проверяется по взаимному расположению векторов, а также их сложением. Так, например,
для используемой в качестве примера схемы (рис. 12):
- векторы токов 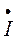 1,
1, 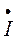 4 и
4 и 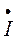 6 и напряжений
6 и напряжений  1,
1,  4 и
4 и  6 совпадают по фазе;
6 совпадают по фазе;
- вектор напряжения  R5 должен совпасть по фазе с вектором I5, а вектор
R5 должен совпасть по фазе с вектором I5, а вектор  L5 опережает вектор тока
L5 опережает вектор тока 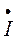 5 на 90
5 на 90  ;
;
- сумма токов узла В 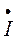 1 и
1 и 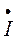 5 соответствии с первым законом Кирхгофа должна быть равна току
5 соответствии с первым законом Кирхгофа должна быть равна току 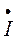 6;
6;
- по второму закону Кирхгофа для контура 111 при сложении векторов напряжений  3,
3,  6 и
6 и  5 должен получиться вектор
5 должен получиться вектор 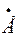 6.
6.
Таким образом может быть выполнена проверка для всех ветвей, узлов и контуров.
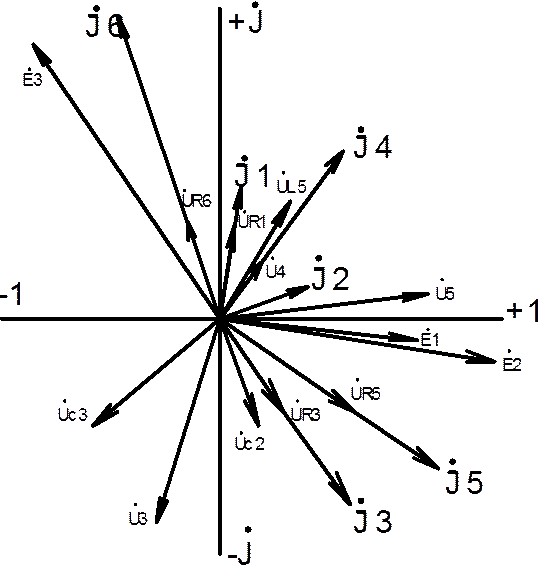
Рис. 13. Векторная диаграмма токов и напряжений для схемы на рис. 12.
Задача 4
4.4.1 Расчет трехфазной цепи не отличается от расчета однофазных цепей с несколькими источниками электроэнергии, имеющими различные начальные фазы. Используя для расчета метод узловых потенциалов, можно определить важные для потребителя электрической энергии величины - фазные напряжения, фазные и линейные токи, напряжение на нейтрали при несимметричных нагрузках, обрыве нулевого провода.
4.4.2 Порядок решения задачи рассмотрен на примере расчета трехфазной четырехпроводной цепи, линейное напряжение которой Uл. = 660 В. Сопротивления нагрузки соединены в звезду и имеют следующие данные: RA = 8 Ом; XLA = 6 Ом; RB = 6 Ом; XBC = 8 Ом;
RC = 23 Ом; XCL = 15,3 Ом. Нулевой провод имеет только активное сопротивление R0 =1 Ом.
Определить:
1) напряжение смещения нейтрали:
а) при наличии нулевого провода;
б) при его обрыве;
2) напряжения на каждой фазе:
а) при наличии нулевого провода;
б) при его обрыве;
3) фазные, линейные токи и ток в нулевом проводе:
а) при наличии нулевого провода;
б) при обрыве нулевого провода
4) при наличии нулевого провода:
а) полную, активную и реактивную мощности каждой фазы и всей цепи;
б) коэффициенты мощности каждой фазы и всей цепи.
Сопротивления обмоток источника питания и фазных проводов не учитывать. Схема включения приемников электрической энергии дана на рис. 14.
Построить векторные диаграммы токов и напряжений:
а) для случая с неповрежденным нулевым проводом;
б) при обрыве нулевого провода;
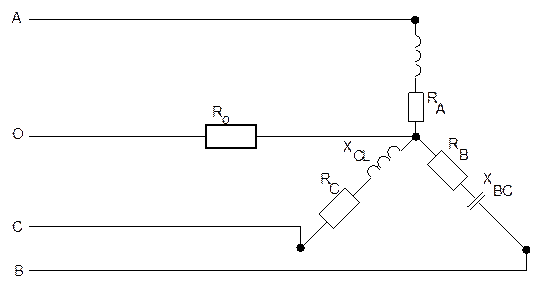
Рис. 14. Схема включения приемников электрической энергии в трехфазную
четырехпроводную цепь.
Решение.
1) Определение напряжения смещения нейтрали.
Напряжение смещения нейтрали U0 может быть найдено методом узловых потенциалов
 0 = (
0 = (  А YA +
А YA +  В YВ +
В YВ +  С YС)/(YА + YВ + YС + Y0),(4.4.1)
С YС)/(YА + YВ + YС + Y0),(4.4.1)
где  А,
А,  В,
В,  С – фазные напряжения фаз А, В и С;
С – фазные напряжения фаз А, В и С;
YА, YВ, YС и Y0 – проводимости фаз А, В, С и нулевого провода.
Все величины должны быть записаны в комплексном виде в алгебраической и показательной формах.
При соединении фаз звездой действующие значения фазных Uф. и линейных Uл. напряжений связаны соотношением
Uф. = Uл./ 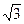 (4.4.2)
(4.4.2)
Таким образом,
UА = UВ = UС = 660/ 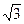 = 380 В.
= 380 В.
Комплексы напряжений, сопротивлений и проводимостей в показательной и алгебраической формах:
 А = 380 е
А = 380 е 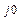 = (380 + j0) В;
= (380 + j0) В;
 В = 380 е
В = 380 е 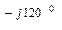 = (-190 – j328) В;
= (-190 – j328) В;
 С = 380 е
С = 380 е 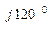 = (-190 + j328) В;
= (-190 + j328) В;
ZА = 8 + j6 = 10 е 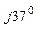 Ом;
Ом;
YА = 1/ ZА = 1/ 10 е 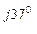 = 0,1 е
= 0,1 е 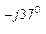 = (0,08 – j0,06) См;
= (0,08 – j0,06) См;
ZВ = 6 – j8 = 10 е 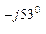 Ом;
Ом;
YВ = 1/ ZВ = 1/10 е 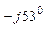 = 0,1 е
= 0,1 е 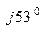 = (0,06 + j0,08) См;
= (0,06 + j0,08) См;
ZС = 23 + j15,3 = 27,6 е 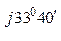 Ом;
Ом;
YС = 1/ZС = 1/27,6 е 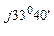 = 0,0362 е
= 0,0362 е 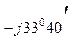 = (0,03 – j0,02) См;
= (0,03 – j0,02) См;
Z0 = 1 + j0 = 1 Ом;
Y0 = 1/ Z0 = 1/1 = 1 См.
Напряжение смещения нейтрали по (4.4.1)
а) при наличии нулевого провода
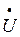 0 = (380 е
0 = (380 е  0,1 е
0,1 е 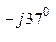 + 380 е
+ 380 е 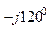 0,1 е
0,1 е 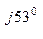 + 380 е
+ 380 е 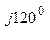 0,0362 е
0,0362 е 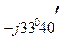 )/
)/
/(0,08 – j0,06 + 0,06 + j0,08 + 0,03 – j0,02 + 1) = (38 е 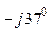 + 38 е
+ 38 е 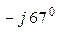 +
+
+ 13,7е 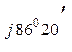 ) / 1,17 = 32,48 е
) / 1,17 = 32,48 е 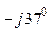 + 32,48 е
+ 32,48 е 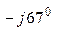 + 11,75 е
+ 11,75 е 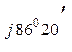 = = 26 – j19,5 +12,7 – j30 + 0,752 + j11,75 = 39,45 – j37,75 = 54 е
= = 26 – j19,5 +12,7 – j30 + 0,752 + j11,75 = 39,45 – j37,75 = 54 е 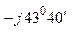 .
.
б) при обрыве нулевого провода
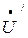 0=(380е
0=(380е 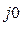 0,1 е
0,1 е 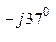 + 380е
+ 380е 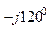 0,1 е
0,1 е 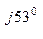 + 380е
+ 380е 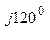 0,0362 е
0,0362 е 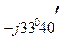 )/
)/
/(0,08 – j0,06 + 0,06 + j0,08 + 0,03 – j0,02) = (38 е 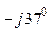 + 38 е
+ 38 е 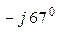 +
+
+ 13,7 е 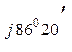 ) / 0,17 = 223,5 е
) / 0,17 = 223,5 е 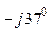 + 223,5 е
+ 223,5 е 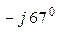 + 80,9 е
+ 80,9 е 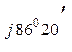 =
=
= 178 – j134 + 87 – j205 + 5,17 + j80,74 = 270 – j258 = 372е 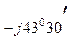 .
.
2) Определение фазных напряжений нагрузки
Напряжение на каждой фазе нагрузки  нагр. является разностью фазного напряжения источника питания
нагр. является разностью фазного напряжения источника питания  и напряжения смещения нейтрали
и напряжения смещения нейтрали 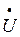 0
0
 нагр. =
нагр. =  -
- 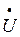 0 (4.4.3)
0 (4.4.3)
Напряжения на фазах нагрузки
а) при наличии нулевого провода
 А нагр.=
А нагр.=  А -
А -  0 = 380 - 39,45 + j37,75 = 340,5 + j37,75 = 348 е
0 = 380 - 39,45 + j37,75 = 340,5 + j37,75 = 348 е 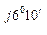 В;
В;
 В нагр. =
В нагр. =  В -
В -  0= -190 – j328 - 39,45 + j37,75= -229,45 - j290,25=370е
0= -190 – j328 - 39,45 + j37,75= -229,45 - j290,25=370е 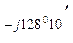 В;
В;
 С нагр.=
С нагр.=  С -
С -  0 = -190 + j328 - 39,45 + j37,75 = -229,45 + j365,75=433 е
0 = -190 + j328 - 39,45 + j37,75 = -229,45 + j365,75=433 е 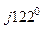 В.
В.
б) при обрыве нулевого провода

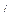 А нагр. =
А нагр. =  А -
А - 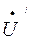 0 = 380 - 270 + j258 = 110 + j258 = 280 е
0 = 380 - 270 + j258 = 110 + j258 = 280 е  В;
В;

 В нагр. =
В нагр. =  В -
В -  0 = -190 – j328 - 270 + j258 = - 460 – j70 = 464 е
0 = -190 – j328 - 270 + j258 = - 460 – j70 = 464 е 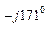 В;
В;

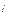 С нагр. =
С нагр. =  С -
С - 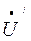 0 = -190 + j 328 - 270 + j258 = - 460 + j586 = 745 е
0 = -190 + j 328 - 270 + j258 = - 460 + j586 = 745 е 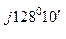 В.
В.
3) Определение фазных и линейных токов, тока в нулевом проводе
При соединении звездой фазные и линейные токи равны, т.е. Iф.А = Iл.А;
Iф.В = Iл.В; Iф.С = Iл.С;
Если известны напряжения  и проводимости Yучастков, токи через них
и проводимости Yучастков, токи через них
можно определить по закону Ома
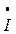 =
=  Y (4.4.4)
Y (4.4.4)
а) Фазные и линейные токи при наличии нулевого провода
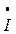 ф.А =
ф.А = 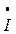 л.А =
л.А =  А нагр. YА = 348 е
А нагр. YА = 348 е 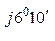 0,1 е
0,1 е 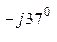 = 34,8 е
= 34,8 е 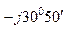 =
=
= (30 – j17,8) А;
 ф.В =
ф.В =  л.В =
л.В =  В нагр. YВ = 370 е
В нагр. YВ = 370 е 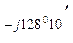 0,1 е
0,1 е 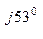 = 37 е
= 37 е 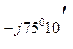 =
=
= (9,35 – j35,7) А;
 ф.С =
ф.С = 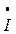 л.С =
л.С =  С нагр. YС = 433 е
С нагр. YС = 433 е 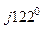 0,0362 е
0,0362 е 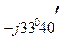 = 15,7 е
= 15,7 е 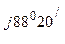 =
=
= (0,45 + j15,6) А
Ток в нулевом проводе
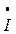 0 =
0 =  0 Y0 = 54 е
0 Y0 = 54 е 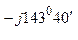 1 = 54 е
1 = 54 е 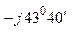 А.
А.
Этот же ток может быть найден по второму закону Кирхгофа
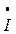 0 =
0 = 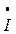 ф.А +
ф.А + 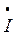 ф.В +
ф.В + 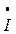 ф.С = 30 – j17,8 + 9,35 – j35,7 + 0,45 + j15,6 = 39,8 - j37,9 = 54 е
ф.С = 30 – j17,8 + 9,35 – j35,7 + 0,45 + j15,6 = 39,8 - j37,9 = 54 е 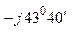 А.
А.
Совпадение результатов подтверждает правильность выполнения расчетов.
б) Фазные и линейные токи при обрыве нулевого провода
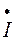
 ф.А =
ф.А = 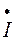
 л.А =
л.А =  А нагр.YА = 280 е
А нагр.YА = 280 е 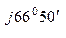 0,1 е
0,1 е 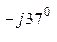 = 28 е
= 28 е 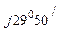 =
=
= (24,2 + j13,95) А;
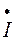
 ф.В =
ф.В = 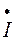
 л.В =
л.В =  В нагр.YВ =464е
В нагр.YВ =464е 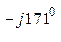 0,1 е
0,1 е 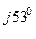 = 46,4 е
= 46,4 е 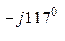 =
=
(- 21,9 – j40,9) А;
 ф.С =
ф.С = 
 л.С =
л.С =  нагр. YС = 745 е
нагр. YС = 745 е 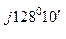 0,0362 е
0,0362 е 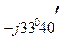 = 27 е
= 27 е 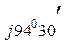 =
=
= (- 2,3 + j26,95) А
Ток в нулевом проводе
 0 =
0 = 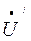 0 Y0 = 0, т.к. при обрыве нулевого провода его проводимость равна
0 Y0 = 0, т.к. при обрыве нулевого провода его проводимость равна
нулю.
4а) Определение мощностей
Полные мощности фаз Sф. находятся как произведение комплексов фазных напряжений  ф. на сопряженные комплексы фазных токов
ф. на сопряженные комплексы фазных токов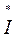 ф.
ф.
S =  ф.
ф. 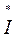 ф.(4.4.5)
ф.(4.4.5)
Сопряженный комплекс какой-либо величины – комплекс этой величины, в котором знак мнимой части заменен на противоположный.
Например: для комплекса фазного тока 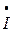 ф.В = 9,35 – j35,7 = 37 е
ф.В = 9,35 – j35,7 = 37 е 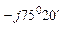 его сопряженный комплекс имеет вид:
его сопряженный комплекс имеет вид:  ф.В = 9,35 + j35,7 = 37 е
ф.В = 9,35 + j35,7 = 37 е 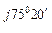 А.
А.
Сопряженные комплексы величин принято обозначать звездочками над их буквенными символами.
Полная мощность каждой фазы по (4.4.5)
SА=  А
А ф.А = 348 е
ф.А = 348 е 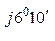 34,8 е
34,8 е 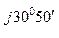 = 11696 е
= 11696 е 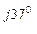 = (9357 + j7017) ВА;
= (9357 + j7017) ВА;
SВ=  В
В ф.В = 370 е
ф.В = 370 е 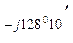 37 е
37 е 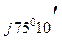 = 13690 е
= 13690 е 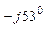 = (8214 – j10952) ВА;
= (8214 – j10952) ВА;
SС=  С
С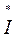 ф.С = 433 е
ф.С = 433 е 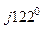 15,7 е
15,7 е 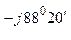 = 6785 е
= 6785 е 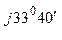 = (5647 + j3757) ВА.
= (5647 + j3757) ВА.
Полная мощность всей нагрузки
S =SА+SВ+ SС = 9357 + j7017 + 8214 – j10952 + 5647 + j3757 = (23218 – j178)ВА.
Активная и реактивная мощности фаз и всей нагрузки находятся как действительная и мнимая части соответствующих комплексов полных мощностей, т.е.
активная мощность фаз
РА = 9357 Вт;
РВ = 8214 Вт;
РС = 5647 Вт;
активная мощность всей нагрузки
Р = РА + РВ + РС = 9357 + 8214 + 5647 = 23218 Вт;
реактивная мощность фаз
QА = 7017 вар;
QВ = -10952 вар;
QС = 3757 вар;
реактивная мощность всей нагрузки
Q = QА + QВ + QС = 7017 -10952 + 3757 = -178 вар.
Активная мощность каждой фазы может быть также найдена по выражению
Рф. = I 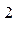 ф. Rф. ,(4.4.6)
ф. Rф. ,(4.4.6)
где Iф. – действующее значение фазного тока;
Rф. – активное сопротивление фазы.
Тогда
РА = I 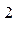 ф.А Rф.А =(34,8)
ф.А Rф.А =(34,8) 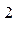 8 = 9357 Вт;
8 = 9357 Вт;
РВ = I 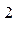 ф.В Rф.В = (37)
ф.В Rф.В = (37) 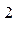 6 = 8214 Вт;
6 = 8214 Вт;
РС = I 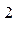 ф.С Rф.С = (15,7)
ф.С Rф.С = (15,7) 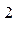 23 = 5647 Вт.
23 = 5647 Вт.
4б) Определение коэффициентов мощности
Коэффициент мощности сos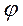 является отношением действительных частей комплексов полной мощности или полного сопротивления к их модулям
является отношением действительных частей комплексов полной мощности или полного сопротивления к их модулям
сos 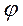 = a/А,(4.4.7)
= a/А,(4.4.7)
где а – действительная часть комплекса;
А – модуль величины.
Таким образом, коэффициенты мощности фаз, найденные с использованием различных величин, при правильном решении должны совпасть.
Коэффициенты мощности фаз
сos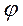 А = РА/SА = 9357/11696 = 0,8, или сos
А = РА/SА = 9357/11696 = 0,8, или сos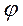 А = RА/ZА = 8/10 = 0,8
А = RА/ZА = 8/10 = 0,8
сos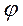 В = РВ/SВ = 8214/13690 = 0,6, или сos
В = РВ/SВ = 8214/13690 = 0,6, или сos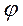 В = RВ/ZВ = 6/10 = 0,6
В = RВ/ZВ = 6/10 = 0,6
сos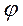 С = РС/SС = 5647/6785 = 0,8323, или сos
С = РС/SС = 5647/6785 = 0,8323, или сos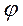 С = RС/ZС = 23/27,6 = 0,8333
С = RС/ZС = 23/27,6 = 0,8333
(Несовпадение значений сos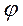 С в третьем знаке вызвано округлением чисел при расчетах).
С в третьем знаке вызвано округлением чисел при расчетах).
Средний коэффициент мощности нагрузки находится по мощности всей цепи
сos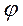 нагр. ср. = Р/S = 23218/
нагр. ср. = Р/S = 23218/ 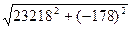 = 23218/23218,7 =1,0
= 23218/23218,7 =1,0
Полученные при расчете данные сведены в таблицу 8.
Таблица 8 - Результаты расчета трехфазной четырехпроводной цепи
