Одноканальная СМО с ожиданием
Рассмотрим простейшую СМО с ожиданием — одноканальную систему 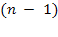 , в которую поступает поток заявок с интенсивностью
, в которую поступает поток заявок с интенсивностью  ; интенсивность обслуживания
; интенсивность обслуживания 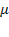 (т. е. в среднем непрерывно занятый канал будет выдавать
(т. е. в среднем непрерывно занятый канал будет выдавать 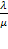 обслуженных заявок в единицу (времени). Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
обслуженных заявок в единицу (времени). Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
Система с ограниченной длиной очереди. Предположим сначала, что количество мест в очереди ограничено числом 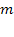 , т. е. если заявка пришла в момент, когда в очереди уже стоят
, т. е. если заявка пришла в момент, когда в очереди уже стоят 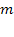 заявок, она покидает систему необслуженной. В дальнейшем, устремив
заявок, она покидает систему необслуженной. В дальнейшем, устремив 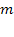 к бесконечности, мы получим характеристики одноканальной СМО без ограничений длины очереди.
к бесконечности, мы получим характеристики одноканальной СМО без ограничений длины очереди.
Будем нумеровать состояния СМО по числу заявок, находящихся в системе (как обслуживаемых, так и ожидающих обслуживания):
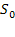 —канал свободен;
—канал свободен;
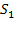 —канал занят, очереди нет;
—канал занят, очереди нет;
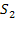 — канал занят, одна заявка стоит в очереди;
— канал занят, одна заявка стоит в очереди;
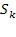 —канал занят,
—канал занят, 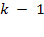 заявок стоят в очереди;
заявок стоят в очереди;
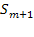 — канал занят, т заявок стоят в очереди.
— канал занят, т заявок стоят в очереди.
ГСП показан на рис. 5.8. Все интенсивности потоков событий, переводящих в систему по стрелкам слева направо, равны  , а справа налево —
, а справа налево — 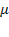 . Действительно, по стрелкам слева направо систему переводит поток заявок (как только придет заявка, система переходит в следующее состояние), справа же налево — поток «освобождений» занятого канала, меющий интенсивность
. Действительно, по стрелкам слева направо систему переводит поток заявок (как только придет заявка, система переходит в следующее состояние), справа же налево — поток «освобождений» занятого канала, меющий интенсивность 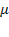 (как только будет обслужена очередная заявка, канал либо освободится, либо уменьшится число заявок в очереди).
(как только будет обслужена очередная заявка, канал либо освободится, либо уменьшится число заявок в очереди).

Рис. 5.8. Одноканальная СМО с ожиданием
Изображенная на рис. 5.8 схема представляет собой схему размножения и гибели. Используя общее решение (5.32)—(5.34), напишем выражения для предельных вероятностей состояний (см. также (5.40)):
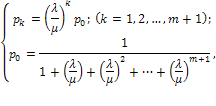
(5.44)
или с использованием 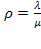 :
:
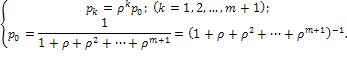
(5.45)
Последняя строка в (5.45) содержит геометрическую прогрессию с первым членом 1 и знаменателем р; откуда получаем:
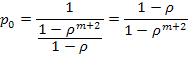
(5.46)
в связи с чем предельные вероятности принимают вид:
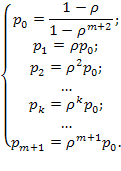
(5.47)
Выражение (5.46) справедливо только при 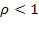 (при
(при 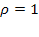 она дает неопределенность вида
она дает неопределенность вида 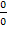 ). Сумма геометрической прогрессии со знаменателем
). Сумма геометрической прогрессии со знаменателем 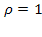 равна
равна 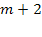 , и в этом случае
, и в этом случае
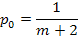
Определим характеристики СМО: вероятность отказа 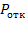 , относительную пропускную способность
, относительную пропускную способность 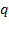 , абсолютную пропускную способность
, абсолютную пропускную способность  , среднюю длину очереди
, среднюю длину очереди  , среднее число заявок, связанных с системой
, среднее число заявок, связанных с системой 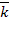 , среднее время ожидания в очереди
, среднее время ожидания в очереди 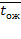 , среднее время пребывания заявки в СМО
, среднее время пребывания заявки в СМО 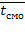
Вероятность отказа. Очевидно, заявка получает отказ только в случае, когда канал занят и все т мест в очереди тоже:
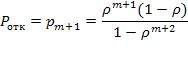
(5.48)
Относительная пропускная способность:
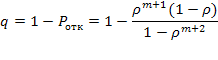
(5.49)
Абсолютная пропускная способность:
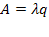
Средняя длина очереди. Найдем среднее число 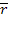 заявок, находящихся в очереди, как математическое ожидание дискретной случайной величины
заявок, находящихся в очереди, как математическое ожидание дискретной случайной величины 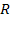 — числа заявок, находящихся в очереди:
— числа заявок, находящихся в очереди:
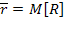
С вероятностью 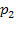 в очереди стоит одна заявка, с вероятностью
в очереди стоит одна заявка, с вероятностью 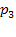 — две заявки, вообще с вероятностью
— две заявки, вообще с вероятностью 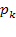 в очереди стоят
в очереди стоят 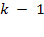 заявок, и т. д., откуда:
заявок, и т. д., откуда:
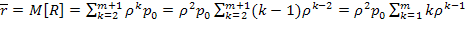 .
.
(5.50)
Поскольку 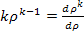 , сумму в (5.50) можно трактовать как производную по
, сумму в (5.50) можно трактовать как производную по 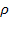 от суммы геометрической прогрессии:
от суммы геометрической прогрессии:
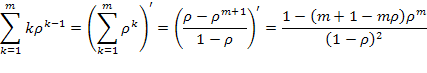
Подставляя данное выражение в (5.50) и используя 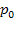 из (5.47), окончательно получаем:
из (5.47), окончательно получаем:
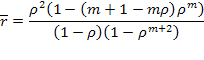
(5.51)
Среднее число заявок, находящихся в системе. Получим далее формулу для среднего числа 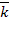 заявок, связанных с системой (как стоящих в очереди, так и находящихся на обслуживании). Поскольку
заявок, связанных с системой (как стоящих в очереди, так и находящихся на обслуживании). Поскольку 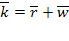 , где
, где 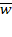 — среднее число заявок, находящихся под обслуживанием, а
— среднее число заявок, находящихся под обслуживанием, а  известно, то остается определить
известно, то остается определить 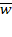 . Поскольку канал один, число обслуживаемых заявок может равняться
. Поскольку канал один, число обслуживаемых заявок может равняться  (с вероятностью
(с вероятностью 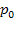 ) или 1 (с вероятностью
) или 1 (с вероятностью 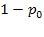 ), откуда:
), откуда:
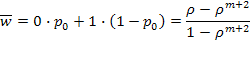
и среднее число заявок, связанных с СМО, равно
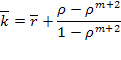
(5.52)
Среднее время ожидания заявки в очереди. Обозначим его 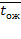 ; если заявка приходит в систему в какой-то момент времени, то с вероятностью
; если заявка приходит в систему в какой-то момент времени, то с вероятностью 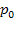 канал обслуживания не будет занят, и ей не придется стоять в очереди (время ожидания равно нулю). С вероятностью
канал обслуживания не будет занят, и ей не придется стоять в очереди (время ожидания равно нулю). С вероятностью 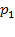 она придет в систему во время обслуживания какой-то заявки, но перед ней не будет очереди, и заявка будет ждать начала своего обслуживания в течение времени
она придет в систему во время обслуживания какой-то заявки, но перед ней не будет очереди, и заявка будет ждать начала своего обслуживания в течение времени 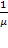 (среднее время обслуживания одной заявки). С вероятностью
(среднее время обслуживания одной заявки). С вероятностью 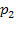 в очереди перед рассматриваемой заявкой будет стоять еще одна, и время ожидания в среднем будет равно
в очереди перед рассматриваемой заявкой будет стоять еще одна, и время ожидания в среднем будет равно 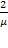 , и т. д.
, и т. д.
Если же 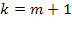 , т. е. когда вновь приходящая заявка застает канал обслуживания занятым и
, т. е. когда вновь приходящая заявка застает канал обслуживания занятым и 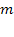 заявок в очереди (вероятность этого
заявок в очереди (вероятность этого 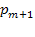 ), то в этом случае заявка не становится в очередь (и не обслуживается), поэтому время ожидания равно нулю. Среднее время ожидания будет равно:
), то в этом случае заявка не становится в очередь (и не обслуживается), поэтому время ожидания равно нулю. Среднее время ожидания будет равно:
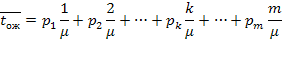
если подставить сюда выражения для вероятностей (5.47), получим:
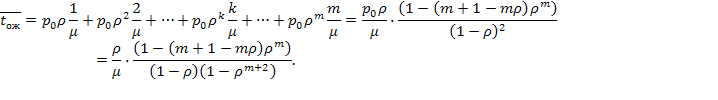
(5.53)
Здесь использованы соотношения (5.50), (5.51) (производная геометрической прогрессии), а также 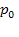 из (5.47). Сравнивая это выражение с (5.51), замечаем, что иначе говоря, среднее время ожидания равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.
из (5.47). Сравнивая это выражение с (5.51), замечаем, что иначе говоря, среднее время ожидания равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.
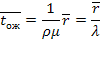
(5.54)
Среднее время пребывания заявки в системе. Обозначим 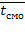 матожидание случайной величины — время пребывания заявки в СМО, которое складывается из среднего времени ожидания в очереди
матожидание случайной величины — время пребывания заявки в СМО, которое складывается из среднего времени ожидания в очереди 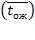 и среднего времени обслуживания
и среднего времени обслуживания 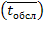 . Если загрузка системы составляет 100 %, очевидно,
. Если загрузка системы составляет 100 %, очевидно, 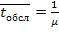 , в противном же случае
, в противном же случае
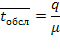
Отсюда
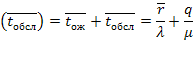
Пример 5.6. Автозаправочная станция (АЗС) представляет собой СМО с одним каналом обслуживания (одной колонкой).
Площадка при станции допускает пребывание в очереди на заправку не более трех машин одновременно 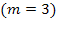 . Если в очереди уже находятся три машины, очередная машина, прибывшая к станции, в очередь не становится. Поток машин, прибывающих для заправки, имеет интенсивность
. Если в очереди уже находятся три машины, очередная машина, прибывшая к станции, в очередь не становится. Поток машин, прибывающих для заправки, имеет интенсивность 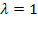 (машина в минуту). Процесс заправки продолжается в среднем 1,25 мин.
(машина в минуту). Процесс заправки продолжается в среднем 1,25 мин.
Определить:
вероятность отказа;
относительную и абсолютную пропускную способности АЗС;
среднее число машин, ожидающих заправки;
среднее число машин, находящихся на АЗС (включая обслуживаемую);
среднее время ожидания машины в очереди;
среднее время пребывания машины на АЗС (включая обслуживание).
иначе говоря, среднее время ожидания равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.
Находим вначале приведенную интенсивность потока заявок:
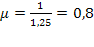 ;
; 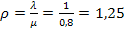 .
.
По формулам (5.47):
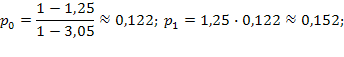
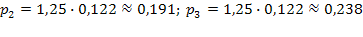
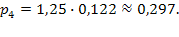
Вероятность отказа 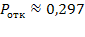 .
.
Относительная пропускная способность СМО
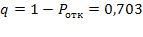 .
.
Абсолютная пропускная способность СМО
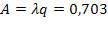 машины в мин.
машины в мин.
Среднее число машин в очереди находим по формуле (5.51)
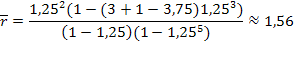
т. е. среднее число машин, ожидающих в очереди на заправку, равно 1,56.
Прибавляя к этой величине среднее число машин, находящихся под обслуживанием
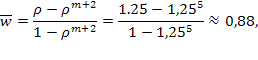
получаем среднее число машин, связанных с АЗС.
Среднее время ожидания машины в очереди по формуле (5.54)
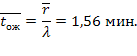
Прибавляя к этой величине 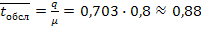 , получим среднее время, которое машина проводит на АЗС:
, получим среднее время, которое машина проводит на АЗС:
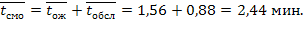
Системы с неограниченным ожиданием. В таких системах значение т не ограничено и, следовательно, основные характеристики могут быть получены путем предельного перехода 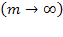 в ранее полученных выражениях (5.44), (5.45) и т. п.
в ранее полученных выражениях (5.44), (5.45) и т. п.
Заметим, что при этом знаменатель в последней формуле (5.45) представляет собой сумму бесконечного числа членов геометрической прогрессии. Эта сумма сходится, когда прогрессия бесконечно убывающая, т. е. при 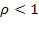 .
.
Может быть доказано, что 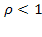 есть условие, при котором в СМО с ожиданием существует предельный установившийся режим, иначе такого режима не существует, и очередь при
есть условие, при котором в СМО с ожиданием существует предельный установившийся режим, иначе такого режима не существует, и очередь при 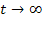 будет неограниченно возрастать. Поэтому в дальнейшем здесь предполагается, что
будет неограниченно возрастать. Поэтому в дальнейшем здесь предполагается, что 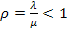 .
.
Если 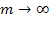 , то соотношения (5.47) принимают вид:
, то соотношения (5.47) принимают вид:
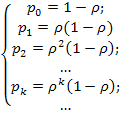
(5.55)
При отсутствии ограничений по длине очереди каждая заявка, пришедшая в систему, будет обслужена, поэтому 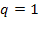 ,
,
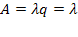
Среднее число заявок в очереди получим из (5.51) при 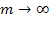 :
:
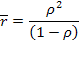
Среднее число заявок в системе по формуле (5.52) при 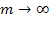
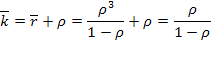
Среднее время ожидания 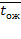 получим из формулы
получим из формулы
(5.53) при 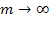 :
:
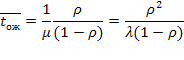
Наконец, среднее время пребывания заявки в СМО есть
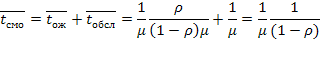
Многоканальная СМО с ожиданием
Система с ограниченной длиной очереди. Рассмотрим 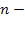 канальную СМО с ожиданием, на которую поступает поток заявок с интенсивностью
канальную СМО с ожиданием, на которую поступает поток заявок с интенсивностью  ; интенсивность обслуживания (для одного канала)
; интенсивность обслуживания (для одного канала) 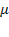 ; число мест в очереди
; число мест в очереди 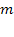 .
.
Состояния системы нумеруются по числу заявок, связанных системой:
нет очереди:
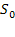 —все каналы свободны;
—все каналы свободны;
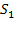 — занят один канал, остальные свободны;
— занят один канал, остальные свободны;
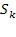 — заняты
— заняты  каналов, остальные нет;
каналов, остальные нет;
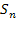 — заняты все
— заняты все  каналов, свободных нет;
каналов, свободных нет;
есть очередь:
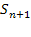 —заняты все n каналов; одна заявка стоит в очереди;
—заняты все n каналов; одна заявка стоит в очереди;
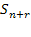 — заняты все n каналов, r заявок в очереди;
— заняты все n каналов, r заявок в очереди;
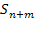 —заняты все n каналов, r заявок в очереди.
—заняты все n каналов, r заявок в очереди.
ГСП приведен на рис. 5.9. У каждой стрелки проставлены соответствующие интенсивности потоков событий. По стрелкам слева направо систему переводит всегда один и тот же поток заявок с интенсивностью  , по стрелкам справа налево систему переводит поток обслуживании, интенсивность которого равна
, по стрелкам справа налево систему переводит поток обслуживании, интенсивность которого равна 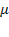 , умноженному на число занятых каналов.
, умноженному на число занятых каналов.

Рис. 5.9. Многоканальная СМО с ожиданием
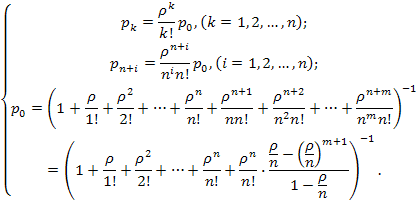
Граф типичен для процессов размножения и гибели, для которой решение ранее получено (5.29)—(5.33). Напишем выражения для предельных вероятностей состояний, используя обозначение 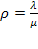 : (здесь используется выражение для суммы геометрической прогрессии со знаменателем
: (здесь используется выражение для суммы геометрической прогрессии со знаменателем 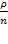 ).
).
Таким образом, все вероятности состояний найдены.
Определим характеристики эффективности системы.
Вероятность отказа. Поступившая заявка получает отказ, если заняты все  каналов и все
каналов и все 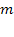 мест в очереди:
мест в очереди:
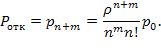
(5.57)
Относительная пропускная способность дополняет вероятность отказа до единицы:
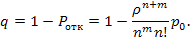
Абсолютная пропускная способность СМО:
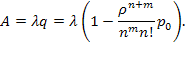
(5.58)
Среднее число занятых каналов. Для СМО с отказами оно совпадало со средним числом заявок, находящихся в системе. Для СМО с очередью среднее число занятых каналов не совпадает со средним числом заявок, находящихся в системе: последняя величина отличается от первой на среднее число заявок, находящихся в очереди.
Обозначим среднее число занятых каналов  . Каждый занятый канал обслуживает в среднем
. Каждый занятый канал обслуживает в среднем 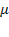 заявок в единицу времени, а СМО в целом обслуживает в среднем
заявок в единицу времени, а СМО в целом обслуживает в среднем  заявок в единицу времени. Разделив одно на другое, получим:
заявок в единицу времени. Разделив одно на другое, получим:
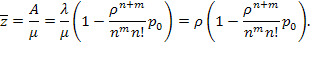
Среднее число заявок в очереди можно вычислить непосредственно как математическое ожидание дискретной случайной величины:
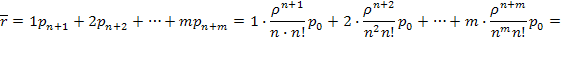
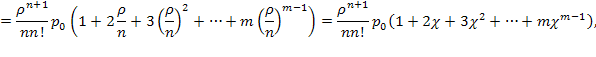
(5.59)
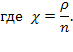
Здесь опять (выражение в скобках) встречается производная суммы геометрической прогрессии (см. выше (5.50), (5.51)—(5.53)), используя соотношение для нее, получаем:
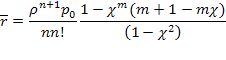
Среднее число заявок в системе:
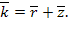
Среднее время ожидания заявки в очереди. Рассмотрим ряд ситуаций, различающихся тем, в каком состоянии застанет систему вновь пришедшая заявка и сколько времени ей придется ждать обслуживания.
Если заявка застанет не все каналы занятыми, ей вообще не придется ждать (соответствующие члены в математическом ожидании равны нулю). Если заявка придет в момент, когда заняты все  каналов, а очереди нет, ей придется ждать в среднем время, равное
каналов, а очереди нет, ей придется ждать в среднем время, равное 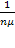 (потому что «поток освобождений»
(потому что «поток освобождений»  каналов имеет интенсивность
каналов имеет интенсивность 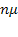 ). Если заявка застанет все каналы занятыми и одну заявку перед собой в очереди, ей придется в среднем ждать в течение времени
). Если заявка застанет все каналы занятыми и одну заявку перед собой в очереди, ей придется в среднем ждать в течение времени 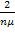 (по
(по 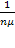 на каждую впереди стоящую заявку) и т. д. Если заявка застанет в очереди
на каждую впереди стоящую заявку) и т. д. Если заявка застанет в очереди  заявок, ей придется ждать в среднем в течение времени
заявок, ей придется ждать в среднем в течение времени 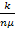 . Если вновь пришедшая заявка застанет в очереди уже
. Если вновь пришедшая заявка застанет в очереди уже 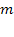 заявок, то она вообще не будет ждать (но и не будет обслужена). Среднее время ожидания найдем, умножая каждое из этих значений на соответствующие вероятности:
заявок, то она вообще не будет ждать (но и не будет обслужена). Среднее время ожидания найдем, умножая каждое из этих значений на соответствующие вероятности:
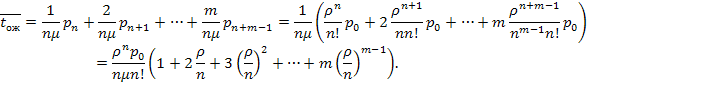
(5.60)
Так же, как и в случае одноканальной СМО с ожиданием, отметим, что это выражение отличается от выражения для средней длины очереди (5.59) только множителем 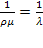 , т. е.
, т. е.
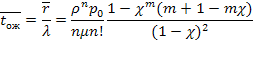
Среднее время пребывания заявки в системе, так же, как и для одноканальной СМО, отличается от среднего времени ожидания на среднее время обслуживания, умноженное на относительную пропускную способность:
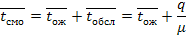
Системы с неограниченной длиной очереди. Мы рассмотрели 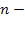 канальную СМО с ожиданием, когда в очереди одновременно могут находиться не более
канальную СМО с ожиданием, когда в очереди одновременно могут находиться не более 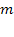 заявок.
заявок.
Так же, как и ранее, при анализе систем без ограничений необходимо рассмотреть полученные соотношения при 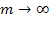 .
.
Вероятности состояний получим из формул (5.56) предельным переходом (при 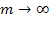 ). Заметим, что сумма соответствующей геометрической прогрессии сходится при
). Заметим, что сумма соответствующей геометрической прогрессии сходится при 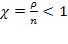 и расходится при
и расходится при 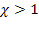 . Допустив, что
. Допустив, что 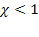 и устремив в формулах (5.56) величину m к бесконечности, получим выражения для предельных вероятностей состояний:
и устремив в формулах (5.56) величину m к бесконечности, получим выражения для предельных вероятностей состояний:
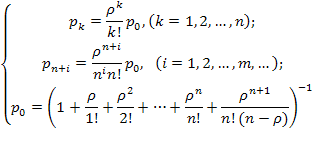
(5.61)
Вероятность отказа, относительная и абсолютная пропускная способность. Так как каждая заявка рано или поздно будет обслужена, то характеристики пропускной способности СМО составят:
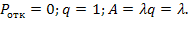
Среднее число заявок в очереди получим при 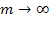 из (5.59):
из (5.59):
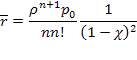
а среднее время ожидания — из (5.60):
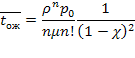
Среднее число занятых каналов  , как и ранее, определяется через абсолютную пропускную способность:
, как и ранее, определяется через абсолютную пропускную способность:
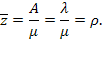
Среднее число заявок, связанных с СМО, определяется как среднее число заявок в очереди плюс среднее число заявок, находящихся под обслуживанием (среднее число занятых каналов):
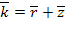
Пример 5.7. Автозаправочная станция с двумя колонками ( 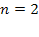 ) обслуживает поток машин с интенсивностью
) обслуживает поток машин с интенсивностью 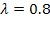 (машин в минуту). Среднее время обслуживания одной машины
(машин в минуту). Среднее время обслуживания одной машины
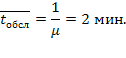
В данном районе нет другой АЗС, так что очередь машин перед АЗС может расти практически неограниченно. Найти характеристики СМО.
Имеем:
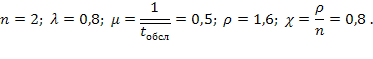
Поскольку 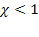 , очередь не растет безгранично и имеет смысл говорить о предельном стационарном режиме работы СМО. По формулам (5.61) находим вероятности состояний:
, очередь не растет безгранично и имеет смысл говорить о предельном стационарном режиме работы СМО. По формулам (5.61) находим вероятности состояний:
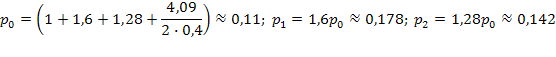
и т. д.
Среднее число занятых каналов найдем, разделив абсолютную пропускную способность СМО 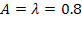 на интенсивность обслуживания
на интенсивность обслуживания 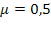 :
:
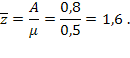
Вероятность отсутствия очереди у АЗС будет:
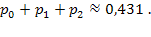
Среднее число машин в очереди:
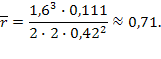
Среднее число машин на АЗС:
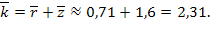
Среднее время ожидания в очереди:
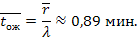
Среднее время пребывания машины на АЗС:
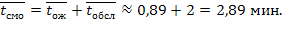
СМО с ограниченным временем ожидания. Ранее рассматривались системы с ожиданием, ограниченным только длиной очереди (числом 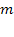 заявок, одновременно находящихся в очереди). В такой СМО заявка, раз ставшая в очередь, не покидает ее, пока не дождется обслуживания. На практике встречаются СМО другого типа, в которых заявка, подождав некоторое время, может уйти из очереди (так называемые «нетерпеливые» заявки).
заявок, одновременно находящихся в очереди). В такой СМО заявка, раз ставшая в очередь, не покидает ее, пока не дождется обслуживания. На практике встречаются СМО другого типа, в которых заявка, подождав некоторое время, может уйти из очереди (так называемые «нетерпеливые» заявки).
Рассмотрим СМО подобного типа, предполагая, что ограничение времени ожидания является случайной величиной.
Предположим, что имеется 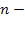 канальная СМО с ожиданием, в которой число мест в очереди не ограничено, но время пребывания заявки в очереди является некоторой случайной величиной со средним значением
канальная СМО с ожиданием, в которой число мест в очереди не ограничено, но время пребывания заявки в очереди является некоторой случайной величиной со средним значением 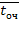 , таким образом, на каждую заявку, стоящую в очереди, действует своего рода пуассоновский «поток уходов» с интенсивностью
, таким образом, на каждую заявку, стоящую в очереди, действует своего рода пуассоновский «поток уходов» с интенсивностью
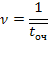
Если этот поток пуассоновский, то процесс, протекающий в СМО, будет марковским. Найдем для него вероятности состояний. Нумерация состояний системы связывается с числом заявок в системе — как обслуживаемых, так и стоящих в очереди:
нет очереди:
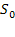 — все каналы свободны;
— все каналы свободны;
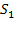 — занят один канал;
— занят один канал;
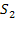 — заняты два канала;
— заняты два канала;
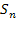 — заняты все
— заняты все  каналов; есть очередь:
каналов; есть очередь:
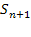 — заняты все
— заняты все  каналов, одна заявка стоит в очереди;
каналов, одна заявка стоит в очереди;
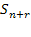 — заняты все
— заняты все  каналов,
каналов,  заявок стоят в очереди и т. д.
заявок стоят в очереди и т. д.
Граф состояний и переходов системы показан на рис. 5.10.

Рис. 5.10. СМО с ограниченным временем ожидания
Разметим этот граф, как и раньше; у всех стрелок, ведущих слева направо, будет стоять интенсивность потока заявок  . Для состояний без очереди у стрелок, ведущих из них справа налево, будет, как и раньше, стоять суммарная интенсивность потока обслуживании всех занятых каналов. Что касается состояний с очередью, то у стрелок, ведущих из них справа налево, будет стоять суммарная интенсивность потока обслуживании всех
. Для состояний без очереди у стрелок, ведущих из них справа налево, будет, как и раньше, стоять суммарная интенсивность потока обслуживании всех занятых каналов. Что касается состояний с очередью, то у стрелок, ведущих из них справа налево, будет стоять суммарная интенсивность потока обслуживании всех  каналов
каналов 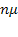 плюс соответствующая интенсивность потока уходов из очереди. Если в очереди стоят
плюс соответствующая интенсивность потока уходов из очереди. Если в очереди стоят  заявок, то суммарная интенсивность потока уходов будет равна
заявок, то суммарная интенсивность потока уходов будет равна 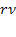 .
.
Как видно из графа, имеет место схема размножения и гибели; применяя общие выражения для предельных вероятностей состояний в этой схеме (используя сокращенные обозначения 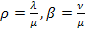 ) запишем:
) запишем:
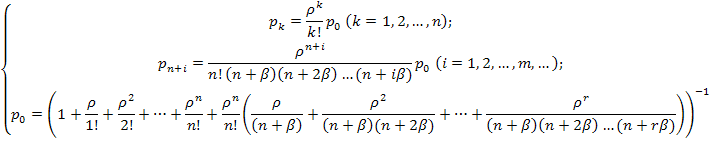
(5.62)
Отметим некоторые особенности СМО с ограниченным ожиданием сравнительно с ранее рассмотренными СМО с «терпеливыми» заявками.
Если длина очереди не ограничена и заявки «терпеливы» (не уходят из очереди), то стационарный предельный режим существует только в случае 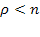 (при соответствующая
(при соответствующая 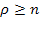 бесконечная геометрическая прогрессия расходится, что физически соответствует неограниченному росту очереди при
бесконечная геометрическая прогрессия расходится, что физически соответствует неограниченному росту очереди при 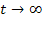 ).
).
Напротив, в СМО с «нетерпеливыми» заявками, уходящими рано или поздно из очереди, установившийся режим обслуживания при 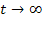 достигается всегда, независимо от приведенной интенсивности потока заявок
достигается всегда, независимо от приведенной интенсивности потока заявок 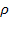 . Это следует из того, что ряд для
. Это следует из того, что ряд для 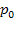 в знаменателе формулы (5.62) сходится при любых положительных значениях
в знаменателе формулы (5.62) сходится при любых положительных значениях 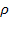 и
и 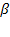 .
.
Для СМО с «нетерпеливыми» заявками понятие «вероятность отказа» не имеет смысла — каждая заявка становится в очередь, но может и не дождаться обслуживания, уйдя раньше времени.
Относительная пропускная способность, среднее число заявок в очереди. Относительную пропускную способность 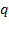 такой СМО можно подсчитать следующим образом. Очевидно, обслужены будут все заявки, кроме тех, которые уйдут из очереди досрочно. Подсчитаем, какое в среднем число заявок покидает очередь досрочно. Для этого вычислим среднее число заявок в очереди:
такой СМО можно подсчитать следующим образом. Очевидно, обслужены будут все заявки, кроме тех, которые уйдут из очереди досрочно. Подсчитаем, какое в среднем число заявок покидает очередь досрочно. Для этого вычислим среднее число заявок в очереди:
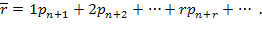
(5.63)
На каждую из этих заявок действует «поток уходов» с интенсивностью  . Значит, из среднего числа
. Значит, из среднего числа  заявок в очереди в среднем будет уходить, не дождавшись обслуживания,
заявок в очереди в среднем будет уходить, не дождавшись обслуживания, 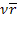 заявок в единицу времени и всего в единицу времени в среднем будет обслуживаться
заявок в единицу времени и всего в единицу времени в среднем будет обслуживаться
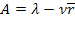
заявок. Относительная пропускная способность СМО будет составлять:
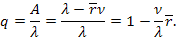
Среднее число занятых каналов  по-прежнему получаем, деля абсолютную пропускную способность
по-прежнему получаем, деля абсолютную пропускную способность  на
на 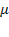 :
:
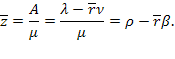
(5.64)
Среднее число заявок в очереди. Соотношение (5.64) позволяет вычислить среднее число заявок в очереди  , не суммируя бесконечного ряда (5.63). Из (5.64) получаем:
, не суммируя бесконечного ряда (5.63). Из (5.64) получаем:
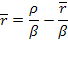
а входящее в эту формулу среднее число занятых каналов можно найти как математическое ожидание случайной величины 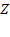 , принимающей значения
, принимающей значения 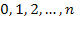 с вероятностями
с вероятностями 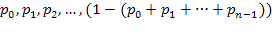 :
:
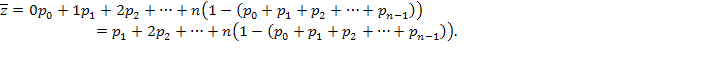
В заключение заметим, что если в формулах (5.62) перейти к пределу при 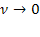 (или, что то же, при
(или, что то же, при 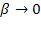 ), то при
), то при 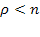 получатся формулы (5.61), т. е. «нетерпеливые» заявки станут «терпеливыми».
получатся формулы (5.61), т. е. «нетерпеливые» заявки станут «терпеливыми».
