По выполнению контрольной работы №1 2 страница
Пример 1. Найти производную функции 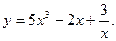
Решение. Данная функция есть алгебраическая сумма функций. Дифференцируем ее, используя формулы 3,5,7 и 8:
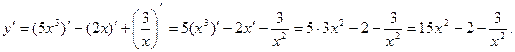
Пример 2. Найти производную функции 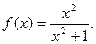
Решение. Применяя формулы 6, 3, 7 и 1, получим
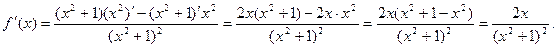
Пример 3. Найти производную функции 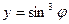 и вычислить ее значение при
и вычислить ее значение при 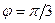 .
.
Решение. Это сложная функция с промежуточным аргументом 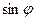 . Используя формулы 7а и 10, имеем
. Используя формулы 7а и 10, имеем 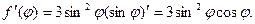
Вычислим значение производной при 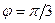 :
:
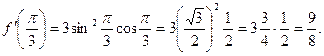
Пример 4. Найти производную функции 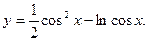
Решение. Это сложная функция с промежуточным аргументом 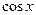 . Применяя формулы 3, 5, 7а, 11, 16а, получим
. Применяя формулы 3, 5, 7а, 11, 16а, получим
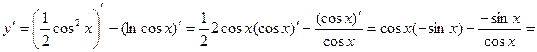
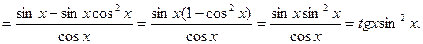
Пример 5. Найти производную функции 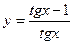 .
.
Решение. Дифференцируем данную функцию по формулам 6, 12, 3 и 1:
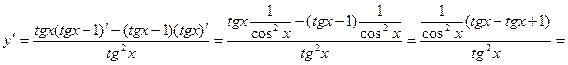
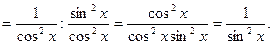
Пример 6. Найти производную функции 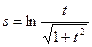 и вычислить ее значение при
и вычислить ее значение при 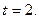
Решение. Сначала преобразуем функцию, используя свойства логарифмов
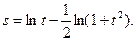
Теперь дифференцируем по формулам 3, 16а, 7 и 1:
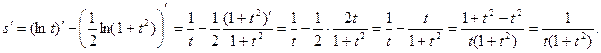
Вычислим значение производной при 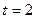
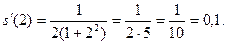
Пример 7. Найти производную функции 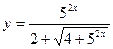 и вычислить ее значение при
и вычислить ее значение при 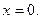
Решение. Используем формулы 6, 3, 14а, 9а, 5 и 1:
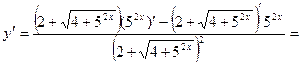
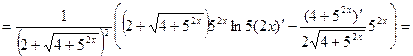
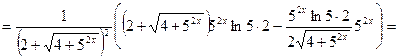
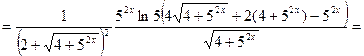
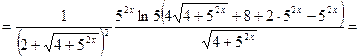
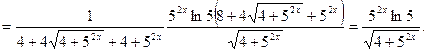
Вычислим значение производной при 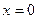 :
:
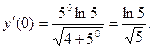
Геометрический смысл производной. Производная функции имеет простую и важную геометрическую интерпретацию.
Если функция 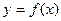 дифференцируема в точке
дифференцируема в точке  , то график этой функции имеет в соответствующей точке касательную, причем угловой коэффициент касательной равен значению производной в рассматриваемой точке.
, то график этой функции имеет в соответствующей точке касательную, причем угловой коэффициент касательной равен значению производной в рассматриваемой точке.
Угловой коэффициент касательной, проведенной к графику функции 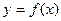 в точке
в точке 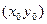 , равен значению производной функции при
, равен значению производной функции при  , т.е.
, т.е. 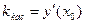 .
.
Уравнение этой касательной имеет вид
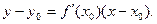
Пример 8. Составить уравнение касательной к графику функции 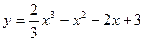 в точке
в точке 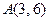 .
.
Решение. Для нахождения углового коэффициента касательной найдем производную данной функции:
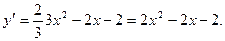
Угловой коэффициент касательной равен значению производной функции при 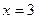 :
:
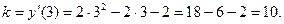
Уравнение касательной имеет вид
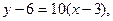 или
или 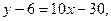 т.е.
т.е. 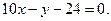
Пример 9. Составить уравнение касательной, проведенной к графику функции 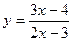 в точке с абсциссой
в точке с абсциссой 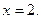
Решение. Сначала найдем ординату точки касания 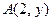 . Так как точка
. Так как точка 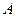 лежит на кривой, то ее координаты удовлетворяют уравнению кривой, т.е.
лежит на кривой, то ее координаты удовлетворяют уравнению кривой, т.е.
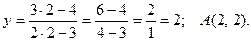
Уравнение касательной, проведенной к кривой в точке 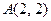 , имеет вид
, имеет вид 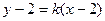 . Для нахождения углового коэффициента касательной найдем производную:
. Для нахождения углового коэффициента касательной найдем производную:
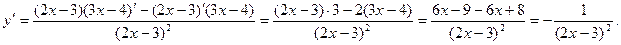
Угловой коэффициент касательной равен значению производной функции при 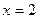 :
:
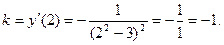
Уравнение касательной таково:
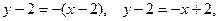 т.е.
т.е. 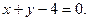
Физический смысл производной. Если тело движется по прямой по закону 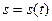 , то за промежуток времени
, то за промежуток времени 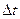 (от момента
(от момента 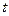 до момента
до момента 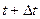 ) оно пройдет некоторый путь
) оно пройдет некоторый путь 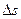 . Тогда
. Тогда 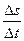 есть средняя скорость движения за промежуток времени
есть средняя скорость движения за промежуток времени 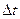 .
.
Скоростью движения тела в данный момент времени 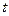 называется предел отношения приращения пути
называется предел отношения приращения пути 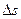 к приращению времени
к приращению времени 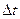 , когда приращение времени стремится к нулю:
, когда приращение времени стремится к нулю:
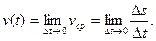
Следовательно, производная пути 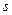 по времени
по времени 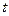 равна скорости прямолинейного движения тела в данный момент времени:
равна скорости прямолинейного движения тела в данный момент времени:
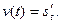
Скорость протекания физических, химических и других процессов также выражается с помощью производной.
Производная функции 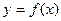 равна скорости изменения этой функции при данном значении аргумента
равна скорости изменения этой функции при данном значении аргумента  :
:
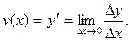
Пример 10. Закон движения точки по прямой задан формулой 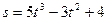 (
( 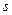 – в метрах,
– в метрах, 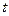 – в секундах). Найти скорость движения точки в конце первой секунды.
– в секундах). Найти скорость движения точки в конце первой секунды.
Решение. Скорость движения точки в данный момент времени равна производной пути 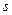 по времени
по времени 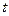 :
:
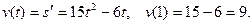
Итак, скорость движения точки в конце первой секунды, равна 9 м/с.
Пример 11. Тело, брошенное вертикально вверх, движется по закону 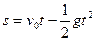 , где
, где 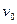 – начальная скорость,
– начальная скорость, 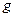 – ускорение свободного падения тела. Найти скорость этого движения для любого момента времени
– ускорение свободного падения тела. Найти скорость этого движения для любого момента времени 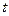 . Сколько времени будет подниматься тело и на какую высоту оно поднимется, если
. Сколько времени будет подниматься тело и на какую высоту оно поднимется, если 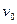 = 40 м/с?
= 40 м/с?
Решение. Скорость движения точки в данный момент времени 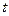 равна производной пути
равна производной пути 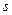 по времени
по времени 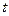 :
:
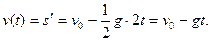
В высшей точке подъема скорость тела равна нулю:
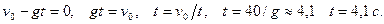
За 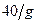 секунд тело поднимется на высоту
секунд тело поднимется на высоту
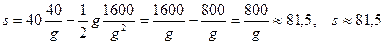 м.
м.
Вторая производная. Производная функции 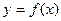 в общем случае является функцией от
в общем случае является функцией от  . Если от этой функции вычислить производную, то получим производную второго порядка или вторую производную функции
. Если от этой функции вычислить производную, то получим производную второго порядка или вторую производную функции 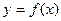 .
.
Второй производной функции 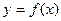 называется производная от ее первой производной
называется производная от ее первой производной 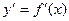 .
.
Вторая производная функции обозначается одним из символов – 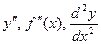 . Таким образом,
. Таким образом, 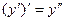 .
.
Аналогично определяются и обозначаются производные любого порядка. Например, производная третьего порядка:
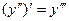 или
или 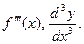
Пример 12. Найти вторую производную функции 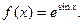
Решение. Сначала найдем первую производную
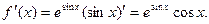
Дифференцируя еще раз, найдем вторую производную:
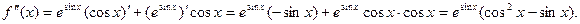
Пример 13. Найти вторую производную функции 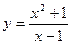 и вычислить ее значение при
и вычислить ее значение при 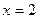 .
.
Решение. Сначала найдем первую производную:
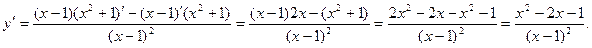
Дифференцируя еще раз, найдем вторую производную:
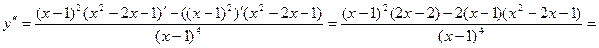
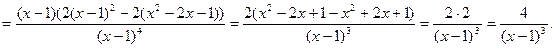
Вычислим значение второй производной при 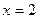 ; имеем
; имеем 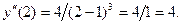
Физический смысл второй производной. Если тело движется прямолинейно по закону 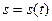 , то вторая производная пути
, то вторая производная пути 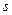 по времени
по времени 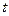 равна ускорению движения в данный момент времени
равна ускорению движения в данный момент времени 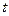 :
:
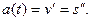
Таким образом, первая производная характеризует скорость некоторого процесса, а вторая производная – ускорение того же процесса.
Пример 14. Точка движется по прямой по закону 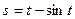 . Найти скорость и ускорение движения при
. Найти скорость и ускорение движения при 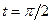 .
.
Решение. Скорость движения тела в данный момент времени равна производной пути 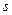 по времени
по времени 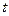 , а ускорение – второй производной пути
, а ускорение – второй производной пути 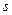 по времени
по времени 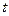 . Находим:
. Находим:
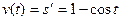 ; тогда
; тогда 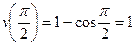 ;
;
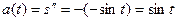 ; тогда
; тогда 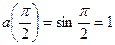 .
.
Пример 15. Скорость прямолинейного движения пропорциональна квадратному корню из пройденного пути (как, например, при свободном падении). Доказать что это движение происходит под действием постоянной силы.
Решение. По закону Ньютона, сила 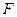 , вызывающая движение, пропорциональна ускорению, т.е.
, вызывающая движение, пропорциональна ускорению, т.е.
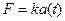 или
или 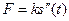 .
.
Согласно условию, 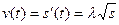 . Дифференцируя это равенство, найдем
. Дифференцируя это равенство, найдем
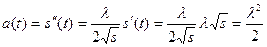 .
.
Следовательно, действующая сила 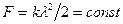 .
.
Приложения производной к исследованию функций.
Условие постоянства функции. Дифференцируемая функция 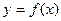 постоянна на промежутке
постоянна на промежутке  тогда и только тогда, когда
тогда и только тогда, когда 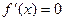 внутри
внутри  .
.
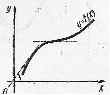 | 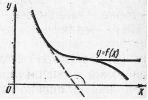 |
| Рис. 5 | Рис. 6 |
Условие возрастания функции. Дифференцируемая функция 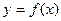 монотонно возрастает на промежутке
монотонно возрастает на промежутке  тогда и только тогда, когда ее производная не отрицательна внутри этого промежутка:
тогда и только тогда, когда ее производная не отрицательна внутри этого промежутка: 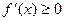 , причем производная
, причем производная 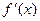 обращается в нуль в конечном числе точек, лежащих внутри промежутка
обращается в нуль в конечном числе точек, лежащих внутри промежутка  .
.
Это условие геометрически означает, что касательная к графику монотонно возрастающей функции образует с положительным направлением оси 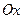 острый угол или параллельна ей. (рис. 5).
острый угол или параллельна ей. (рис. 5).
Условие убывания функции. Дифференцируемая функция 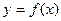 монотонно убывает на промежутке
монотонно убывает на промежутке  тогда и только тогда, когда ее производная не положительна внутри этого промежутка:
тогда и только тогда, когда ее производная не положительна внутри этого промежутка: 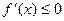 , причем производная
, причем производная 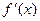 обращается в нуль в конечном числе точек, лежащих внутри
обращается в нуль в конечном числе точек, лежащих внутри  .
.
Это условие геометрически означает, что касательная к графику монотонно убывающей функции образует с положительным направлением оси 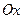 тупой угол или параллельна ей (рис. 6).
тупой угол или параллельна ей (рис. 6).
Экстремумы функции. Говорят, что функция 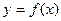 имеет максимум в точке
имеет максимум в точке 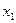 (рис. 7), если значение функции в этой точке больше, чем ее значения во всех точках,, достаточно близких к
(рис. 7), если значение функции в этой точке больше, чем ее значения во всех точках,, достаточно близких к 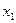 , т.е. если
, т.е. если 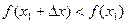 для любых
для любых  , как положительных, так и отрицательных, но достаточно малых по модулю. Таким образом,
, как положительных, так и отрицательных, но достаточно малых по модулю. Таким образом, 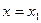 – точка максимума, а
– точка максимума, а 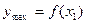 – максимум функции.
– максимум функции.
Говорят, что функция 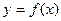 имеет минимум в точке
имеет минимум в точке 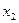 (рис. 7), если значение функции в этой точке меньше, чем ее значение во всех точках, достаточно близких к
(рис. 7), если значение функции в этой точке меньше, чем ее значение во всех точках, достаточно близких к 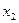 , т.е. если
, т.е. если 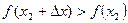 для любых
для любых  , как положительных, так и отрицательных, но достаточно малых по модулю. Таким образом,
, как положительных, так и отрицательных, но достаточно малых по модулю. Таким образом, 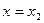 – точка минимума, а
– точка минимума, а 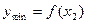 – минимум функции.
– минимум функции.
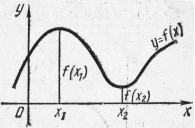 Рис. 7 Рис. 7 | Если в некоторой точке функция имеет максимум или минимум, то говорят, что в этой точке имеет место экстремум. Значение функции в этой точке называется экстремальным. Замечание. Следует помнить: 1) что максимум (минимум) не является обязательно наибольшим (наименьшим) значением, принимаемым функцией; 2) функция может иметь несколько максимумов или |
минимумов; 3) функция, определенная на отрезке, может достигать экстремума только во внутренних точках этого отрезка.
Необходимое условие экстремума. Если функция 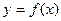 имеет экстремум при
имеет экстремум при  , то ее производная в этой точке равна нулю или бесконечности, либо вовсе не существует, при этом сама функция в точке
, то ее производная в этой точке равна нулю или бесконечности, либо вовсе не существует, при этом сама функция в точке 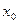 определена.
определена.
Из этого следует, что точки экстремума функции следует разыскивать только среди тех, в которых ее первая производная равна нулю, или бесконечности, или не существует. Эти точки называются критическими точками I рода.
Этот признак экстремума является только необходимым. Поэтому, определив критические точки I рода, надо каждую из них в отдельности исследовать на основании достаточных условий экстремума.
Первое достаточное условие существования экстремума функции. Пусть точка  является критической точкой I рода функции
является критической точкой I рода функции 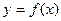 , а сама функция дифференцируема во всех точках некоторого промежутка, содержащего эту точку (за исключением, возможно, самой точки). Тогда:
, а сама функция дифференцируема во всех точках некоторого промежутка, содержащего эту точку (за исключением, возможно, самой точки). Тогда:
1) если при переходе слева направо через критическую точку I рода  первая производная меняет знак с плюса на минус, то в этой точке функция достигает максимума, т.е.
первая производная меняет знак с плюса на минус, то в этой точке функция достигает максимума, т.е.  – точка максимума,
– точка максимума, 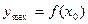 ;
;
2) если при переходе слева направо через критическую точку I рода  первая производная меняет знак с минуса на плюс, то в этой точке функция достигает минимума, т.е.
первая производная меняет знак с минуса на плюс, то в этой точке функция достигает минимума, т.е.  – точка минимума,
– точка минимума, 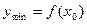 ;
;
3) если при переходе через критическую точку I рода первая производная не меняет знака, то в этой точке экстремума нет.
Для исследования функции на экстремум по первой производной следует:
1. Найти область определения функции.
2. Найти первую производную функции и критические точки I рода.
3. Отметить границы области определения и критические точки I рода на числовой прямой.
4. Исследовать знак производной в каждом из полученных интервалов.
5. Выписать точки экстремума и вычислить экстремумы функции.
Пример 16. Найти экстремумы функции 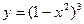 .
.
Решение. 1. Областью определения функции служит множество всех действительных чисел, т.е. 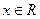 .
.
2. Функция имеет производную всюду, поэтому определяем критические точки из условия 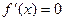 . Находим производную:
. Находим производную:
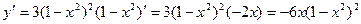 ;
;
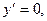
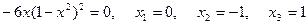
3. Отмечаем эти критические точки на числовой прямой (рис. 8).
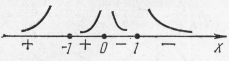 Рис. 8. Рис. 8. | 4. Исследуем знак производной 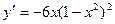 в каждом из полученных интервалов: в каждом из полученных интервалов: 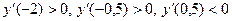 , , 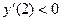 . . |
5. точка 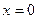 – точка максимума, так как при переходе через нее слева направо производная меняет знак с плюса на минус:
– точка максимума, так как при переходе через нее слева направо производная меняет знак с плюса на минус: 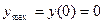 . Точки
. Точки 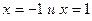 не являются точками экстремума.
не являются точками экстремума.
Второе достаточное условие существования экстремума функции. Если в точке  первая производная равна нулю
первая производная равна нулю 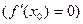 , а вторая производная отличная от нуля, то
, а вторая производная отличная от нуля, то  – точка экстремума.
– точка экстремума.
При этом если вторая производная в этой точке положительна 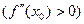 , то
, то  – точка минимума; если вторая производная в этой точке отрицательна
– точка минимума; если вторая производная в этой точке отрицательна 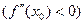 , то
, то  – точка максимума.
– точка максимума.
Для исследования функции на экстремум по первой и второй производной следует:
1. Найти область определения функции.
2. Найти первую производную функции и стационарные точки, т. е. точки, в которых она обращается в нуль.
3. Найти вторую производную функции и исследовать ее знак в каждой стационарной точке.
4. Выписать точки экстремума и вычислить (если нужно) экстремумы функции.
Пример 17. Найти экстремумы функции 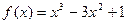 .
.
