Решение систем линейных уравнений

Действия с векторами.

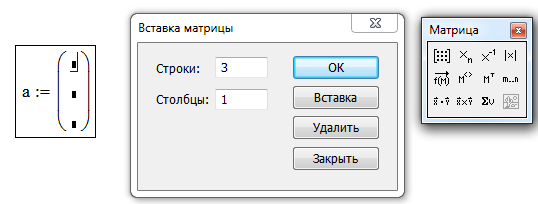
Работать с векторами в пакете MathCAD нужно с помощью панели инструментов Matrix (кнопка ). Появится окно, изображенное на рис. 3.1.

Рисунок 3.1

При вводе опции ORIGIN:=1 нумерация строк начинается с единицы. По умолчанию нумерация начинается с нуля. Линейная комбинация векторов осуществляется обычным способом алгебраических преобразований. Вычисление модуля вектора, скалярного и векторного произведения векторов осуществляется с помощью соответствующих кнопок панели Matrix (рис. 3.1). На этой панели 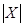- вычисление модуля, 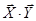- скалярное произведение, 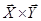- векторное произведение.

Решение уравнений.

Пример 1. Найти корни полинома _.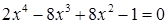

Решим это уравнение с помощью функции polyroots (рис. 3.2). Массив коэффициентов, используемый в этой функции, определим как вектор-столбец из пяти элементов. Обратите внимание, что в уравнении отсутствует переменная х в первой степени. Это означает, что соответствующий коэффициент равен нулю.

Рисунок 3.2

Как видно из проверки, при подстановке в данное уравнение первого вычисленного корня (х1) получается верное равенство, при подстановке других корней верное равенство получается лишь приблизительно, так как корни этого уравнения - числа иррациональные.

Пример 2. Найти корни уравнения .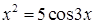

Уравнение произвольного вида решается с помощью функции root.

Решение.

1. Перенесем выражение, стоящее в правой части в левую, получим _.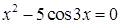

2. Введем функцию 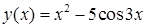. Корни данного уравнения - точки пересечения функции y(х) с осью абсцисс.

3. Построим график функции на таком интервале переменной х , чтобы четко наблюдались корни уравнения (рис. 3.3). Так как функция y(х) четная, то достаточно строить графики только при положительных значениях переменной х. Из рисунка видно, на втором графике корни уравнения более различимы.

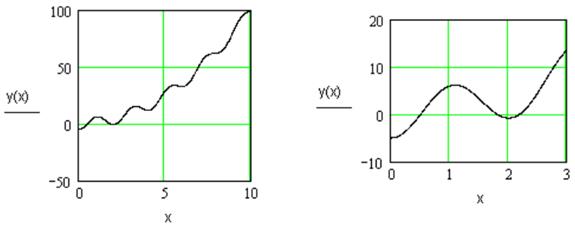Рисунок 3.3

4. Определим интервалы изоляции корней по второму графику (рис. 3.3). Первый корень лежит на интервале (0; 1), второй - на участке (1; 2), третий - (2; 3). Уточним корни уравнения с помощью функции root (рис. 3.4).

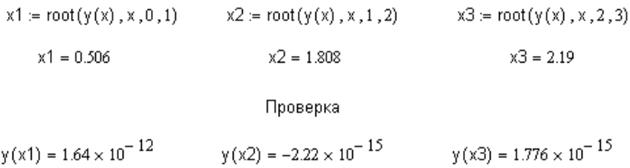Рисунок 3.4

Ответ: х = -2.19, -1.808, -0.506, 0.506, 1.808, 2.19.

Прим е р 3. Найти значение абсциссы и ординаты экстремумов функции .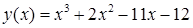

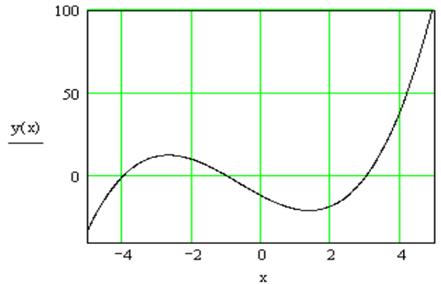
Решение. Перед нахождением экстремумов нужно определить промежуток оси абсцисс, где они находятся. Для этого строим график данной функции на произвольном отрезке (рис. 3.5). Если на построенном промежутке экстремумов нет, его нужно поменять. Строим график функции 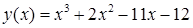на участке [-5; 5].

Рисунок 3.5

Как видно из рис. 3.5, минимум функции находится вблизи точки х = 2, а максимум - вблизи точки х = -3. Точки экстремума вычисляются с помощью функций Minimize (минимум) или Maximize (максимум), но перед ними необходимо написать слово Given (рис. 3.6).

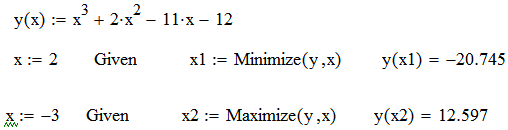Рисунок 3.6

Ответ: минимум (1,361; -20,745); максимум (-2,694; 12,597).

Решение систем линейных уравнений.

Пример 4. Решить систему уравнений

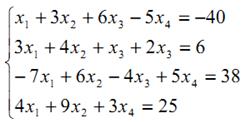Данную систему можно рассматривать как одно матричное уравнени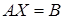е , где 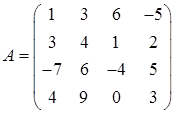, 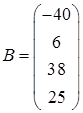. Поэтому уравнение можно решить традиционным матричным способом (рис. 3.7).

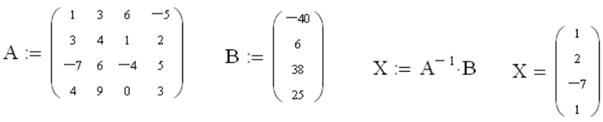Рисунок 3.7

Ответ: х1=1, х2=2, х3=-7, х4=1.