Постановка и решение задачи линейной регрессии. Метод наименьших квадратов
Рассмотрим 2 случайные величины X и Y, заданные на одном и том же пространстве элементарных событий. Значениям 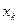 и
и 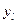 этих случайных величин соответствуют вероятности P
этих случайных величин соответствуют вероятности P 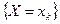 и P
и P 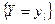 , с которыми они принимаются.
, с которыми они принимаются.
Пусть каждой паре ( 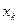 ,
, 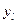 ) соответствует вероятность p(
) соответствует вероятность p( 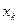 ,
, 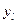 ) того, что
) того, что 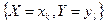 . Тогда говорят, что задано совместное распределение случайных величин X и Y.
. Тогда говорят, что задано совместное распределение случайных величин X и Y.
Случайные величины называются независимыми, если для любых 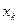 ,
, 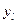 справедливо равенство p(
справедливо равенство p( 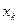 ,
, 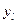 )=P
)=P 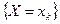 P
P 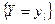 .
.
По определению их ковариация равна Cov(X, Y)=M((X-MX)(Y-MY)), где буквой М обозначено мат.ожидание.
Через ρ(X, Y) будем обозначать коэффициент корреляции X и Y, который определяется как ρ(X, Y)= 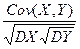 , где DX, DY – дисперсии X и Y. Если случайные величины независимы, их ковариация равна нулю. Заметим, что обратное неверно: равенство нулю ковариации и коэффициента корреляции еще не гарантирует независимости случайных величин. Из определения и неравенства Коши-Буняковского следует, что коэффициент корреляции принимает значения между -1 и +1.
, где DX, DY – дисперсии X и Y. Если случайные величины независимы, их ковариация равна нулю. Заметим, что обратное неверно: равенство нулю ковариации и коэффициента корреляции еще не гарантирует независимости случайных величин. Из определения и неравенства Коши-Буняковского следует, что коэффициент корреляции принимает значения между -1 и +1.
Будем говорить,что между случайными величинами X и Y имеется функциональная зависимость, если существует функция F(x) такая, что Y=F(x). Если же среднее значение одной случайной величины функционально зависит от значений, принимаемых другой, то будем говорить, что такие случайные величины связаны корреляционной зависимостью.
Выразим функционально один из двух взаимосвязанных факторов через другой (хотя бы приближенно). Простейшим из таких выражений является линейное: Y=aX+b, где a и b – некоторые константы.
Если справедливо равенство, то между X и Y имеется функциональная зависимость, даже линейная. Это бывает лишь в случаях, когда ρ(X, Y)=1 или ρ(X, Y)=-1. Если же –1< ρ(X, Y)<1, равенство может выполняться лишь приближенно, при условии, что константы a и b выбраны некоторым специальным образом.
Их выбирают такими, чтобы функция F(a,b)=M((Y–aX–b) 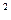 ) достигала в точке a, b минимума. Тогда в среднем квадратичном случайная величина aX+b будет менее всего уклоняться от Y.
) достигала в точке a, b минимума. Тогда в среднем квадратичном случайная величина aX+b будет менее всего уклоняться от Y.
Применив метод наименьших квадратов, найдем для a и b следующие значения:
a= ρ(X, Y) 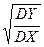 , b=MY – ρ(X, Y)
, b=MY – ρ(X, Y) 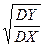 MX
MX
тогда F(a,b)=DY(1 – ρ(X, Y) 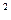 ).
).
1. Если ρ(X, Y)>0, то при увеличении одной из случайных величин другая также имеет тенденцию к увеличению.
2. Если ρ(X, Y) <0, то при увеличении одной из случайных величин другая также будет в среднем квадратичном возрастать.
3. Если ρ(X, Y)=0, то при любых a, b M((Y – aX – b) 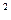 )≥DY. Следовательно, ни при каких a, b случайная величина aX+b не может в среднем квадратичном приблизить случайную величину Y лучше, чем константа MY(среднее значение Y).
)≥DY. Следовательно, ни при каких a, b случайная величина aX+b не может в среднем квадратичном приблизить случайную величину Y лучше, чем константа MY(среднее значение Y).
4. Если –1< ρ(X, Y)<1, то при a,b M((Y–aX–b) 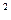 )= DY(1 – ρ(X, Y)
)= DY(1 – ρ(X, Y) 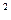 ). Следовательно, случайная величина aX+b в среднем квадратичном лучше приближает Y, чем MY, причем тем лучше, чем больше
). Следовательно, случайная величина aX+b в среднем квадратичном лучше приближает Y, чем MY, причем тем лучше, чем больше 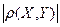 .
.
5. Если ρ(X, Y)=1 или ρ(X, Y)= –1, то равенство Y=aX+b выполняется с вероятностью 1.
Метод наименьших квадратов
Введем обозначения:
m 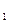 =MX, m
=MX, m 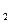 =MY,
=MY, 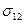 =Cov(X,Y),
=Cov(X,Y), 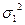 =DX,
=DX, 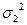 =DY.
=DY.
Пользуясь ими, вычисляем:
F(a,b)= M(Y – aX – b) 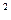 =M((Y – m
=M((Y – m 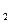 ) – a(X – m
) – a(X – m 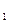 ) + (m
) + (m 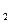 – a m
– a m 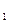 – b))
– b)) 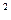 =
= 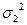 +a
+a 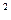
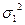 –2a
–2a 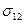 +( m
+( m 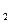 –a m
–a m 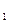 – b)
– b) 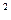 .
.
Исследуем функцию на экстремум. Сначала вычисляем ее частные производные и приравниваем их к нулю:
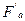 (a,b)=2a
(a,b)=2a 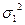 –2
–2 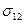 –2 m
–2 m 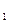 ( m
( m 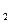 –a m
–a m 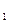 –b)=0
–b)=0
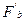 (a,b)=–2(m
(a,b)=–2(m 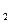 –a m
–a m 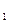 –b)=0
–b)=0
Решая полученную систему линейных уравнений относительно a, b, получаем: a= 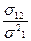 , b= m
, b= m 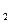 –
– 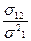 m
m 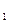 . Вычислим
. Вычислим 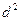 F(a,b)=2(
F(a,b)=2( 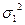 +
+ 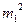 )da
)da 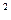 +4 m
+4 m 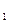 dadb+2db
dadb+2db 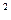 =2
=2 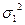 da
da 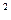 +2(m
+2(m 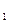 da+db)
da+db) 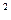 >0. Функция имеет единственную точку экстремума и в этой точке достигается минимум. Отметим, что выражению M(Y – aX – b)
>0. Функция имеет единственную точку экстремума и в этой точке достигается минимум. Отметим, что выражению M(Y – aX – b) 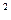 можно придать такой смысл: это среднее значение суммы квадратов расстояний от прямой y=ax+b до значений случайной величины Y, причем расстояние измеряется вдоль оси OY.
можно придать такой смысл: это среднее значение суммы квадратов расстояний от прямой y=ax+b до значений случайной величины Y, причем расстояние измеряется вдоль оси OY.
Основные понятия математической статистики.
МС – наука, которая изучает вероятностные свойства ГС.
Генеральная совокупность (ГС) – совокупность объектов, из которых производится выборка.
Задача МС : изучить вероятн-ые свойства генеральной совокупности.
Выборка – совокупность,случайно отобранных объектов (выборочная совокупность).
Числа выборки, упорядоченные по возрастанию,образуют вариационный ряд:
X 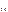 ≤ X
≤ X 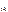 ≤ …≤ X
≤ …≤ X 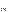
Статистики вида:
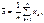
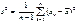
называются соответственно выборочным средним и выборочной дисперсией.
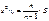 – несмещенная оценка DX (исправленная выборочная дисперсия)
– несмещенная оценка DX (исправленная выборочная дисперсия)
Статистическая оценка – любая функция от выборки. Свойства статистической оценки:
1. Несмещенность
2. Состоятельность
3. Эффективность
Теорема: Оценки  и
и 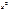 – несмещенные, а оценка
– несмещенные, а оценка  – состоятельная.
– состоятельная.
Доказательство: Сначала докажем несмещенность оценок. Нужно проверить, что M  =a, M
=a, M 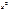 =σ
=σ 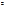 .
.
По определению имеем
 M
M  =M
=M 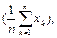 =
= 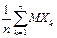 =a.
=a.
Далее,
M 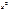 =
= 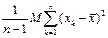 , где
, где 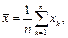
Выполним тождественные преобразования:
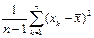 =
= 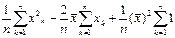 =
= 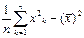 =
= 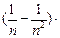
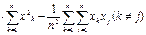
Далее воспользуемся тем, что MX 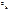 = σ
= σ 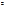 +a
+a 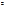 , и при
, и при 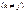 M (X
M (X 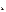 X
X 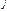 )=MX
)=MX 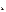 ·MX
·MX 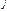 ( случайные величины X
( случайные величины X 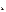 и X
и X 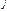 независимы)
независимы)
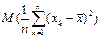 =
= 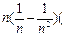 σ
σ 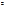 +a
+a 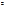 )–
)– 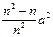 =(1–
=(1– 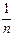 ) σ
) σ 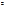 , то есть M
, то есть M 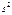 =σ
=σ 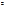 .
.
Докажем состоятельность оценки  . Для этого вычислим D
. Для этого вычислим D  :
:
D  =
= 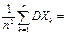
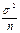 → 0.
→ 0.
Если D  и M
и M  → 0, то
→ 0, то  – состоятельная оценка параметра x.
– состоятельная оценка параметра x.
