Положительные и отрицательные числа

Применение мнемонических правил на уроках математики

Мнемоника (греч. τα μνημονιχα — искусство запоминания) - совокупность специальных приёмов и способов, облегчающих запоминание нужной информации и увеличивающих объём памяти путём образования ассоциаций. Замена абстрактных объектов и фактов на понятия и представления, имеющие визуальное, аудиальное или кинестетическое представление, связывание объектов с уже имеющейся информацией в памяти различных типов для упрощения запоминания.

Алгебра

Натуральные числа

Умножение на 5: дописать 0 и разделить на 2.

Например, 836×5=8360/2=4180

Умножение не 9: дописать 0 и отнять исходное число.

Например, 254×9=2540-254=2286

Умножать на 9 числа от 1 до 10 можно на пальцах. Вытягиваем 10 пальцев. Например, хотим умножить на 3. Загибаем третий палец и считаем вытянутые. Слева их 2, справа 7. Значит 27. И т.п.

Умножение на 9 от 1 до 9: пишем столбиком цифры от нуля до 8, а снизу вверх рядом от 1 до 9:

Умножение двузначных чисел на 11: записываем число, а в середину вставляем сумму его цифр. Например, 24×11=2#4 (вместо решетка сумма цифр)=2 (2+4) 4=264. Если сумма цифр больше 10, то вторая цифра записывается в середину, а десятки прибавляются к первой цифре. Например, 75×11=7#5=7 (7+5) 5=(7+1) 25=825

О нуле

Когда-то многие считали, что нуль не значит ничего

И, как ни странно, полагали, что нуль совсем не есть число.

Но на оси средь прочих чисел он все же место получил,

И все действительные числа на два разряда разделил.

Нуль не в один из них не входит, он сам составил чисел класс,

О всех его особых свойствах мы поведем сейчас рассказ.

Коль нуль к числу ты прибавляешь иль отнимаешь от него

В ответе тотчас получаешь опять то самое число.

Попав как множитель средь чисел, он сводит мигом всех на нет.

И потому в произведенье один за всех несет ответ.

А относительно деления, во первых нужно помнить то,

Что уж давно в научном мире делить на нуль запрещено.

Причина всем ведь очевидна, а состоит причина в том,

Что смысла нет в таком деленьи. Противоречье в нем самом.

И впрямь какое из известных число за частное нам взять,

Когда с нулем в произведенье все числа нуль лишь могут дать?

«а» в нулевой есть единица, так все условились считать.

Но глубоко бы тот ошибся, кто б это вздумал доказать.

Обыкновенные дроби

Каждый может за версту

Видеть дробную черту.

Над чертой – числитель, знайте,

Под чертою – знаменатель.

Дробь такую непременно

Надо звать обыкновенной

Вот дробь три четвёртых.

Нам видно чётко:

В числителе тройка

Меньше четвёрки.

Дробь такая по правилу

Называется правильной.

Если дроби нам такие две даны,

У которых знаменатели равны,

Больше будет та, бесспорно,

Числитель больше у которой.

Умножение дробей обыкновенных

Без ошибки можно выполнить мгновенно.

Надо сразу их числители умножить,

Получается числитель в результате,

Знаменатели потом умножить тоже –

И получим новой дроби знаменатель.

Как деление дробей обыкновенных

Выполняется, запомнить каждый может:

Надо первую из двух и непременно

На обратную второй дроби умножить.

Десятичные дроби

Чтоб десятичные дроби сложить,

Нам не приходится долго мудрить:

Выстроим все запятые мы в ряд,

Цифра под цифрой строго стоят.

И в результате получим мы вновь,

Побольше других, десятичную дробь.

Чтоб две дроби сложить,

Долго думать не надо.

Просто их запиши

Разряд под разрядом.

Дальше складывай числа, -

Совет мой такой, -

И пиши запятую под запятой.

При сложении дробей десятичных

Не отступим от правил обычных.

Пиши запятую под запятой,

Разряд под разрядом – в этом вся соль.

Десятичные дроби вычти, сложи,

Цифру под цифрой строго пиши,

И запятые все сохраняй,

В ряд их пиши, не забывай!

Дроби десятичные когда мы умножаем,

Запятой внимания почти не уделяем.

Здесь работает такое правило:

Умножай их. Как числа натуральные.

Подсчитав в множителях обоих

Знаки, отделённые справа запятою.

Столько же отметь в произведении,

И получишь верное решение.

Чтоб десятичную дробь округлять,

До какого разряда надо бы знать,

Разрядную цифру ты сохрани,

Добавь к ней единицу,

Если первая отбрасываемая цифра пять

Или больше пяти.

Делимость чисел

Можно съесть кило варенья,

Закусить его соленьем,

Не бояться вражьих пуль, -

Но нельзя делить на нуль!

Десятки превратил он в сотни,

А может в миллионы превратить.

Он среди чисел равноправен,

Но на него нельзя делить.

Признаки делимости

Знать обязательно каждому надо,

Чтоб получить без ошибки ответ:

Из натуральных разделятся на два

Чётные числа, нечётные – нет.

Натуральные без всякого труда

Те лишь на три делятся всегда,

У которых сумма цифр, ты посмотри,

Без остатка тоже делится на три.

О том, что не вернуть минуты вспять,

Давно по свету ходит поговорка.

А те лишь числа делятся на пять,

В конце которых ноль или пятёрка.

Принцип нумерологии для делимости на 9 (вспомогательно и для 3):

Девятки в записи числа «пропадают».

Например, 992399921 – проверяем только 2+3+2+1 = 8 – не делится ни на 3, ни на 9.

Простые числа

Хоть есть среди них большие,

Судьба их такова:

Делителей у каждого

Всего лишь только два.

С давних пор числа такие

Называются простые.

Составные числа

Мы эти числа учим тоже.

Делители найти их сможем.

У каждого числа – смотри –

Должно быть их хотя бы три.

Эти числа не простые,

Эти числа составные.

Отношения и пропорции

«Крест накрест» - основное свойство пропорции.

Положительные и отрицательные числа

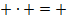
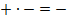
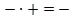
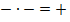
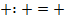
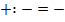
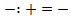
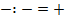
Минус с минусом сложить,

Можно минус получить.

Если сложишь минус, плюс,

То получится конфуз?!

Знак числа ты выбирай

Что сильнее, не зевай!

Модули их отними,

Да все числа помири!

Минус с плюсом множь, дели,

Минус ставь, и не мудри!

«Друг моего друга - мой друг»

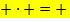
«Друг моего врага - мой враг»