Полиномы, наименее уклоняющиеся от нуля

(полиномы Чебышева на промежутке).

Полиномы Чебышева, рассматриваемые ранее, применялись для аппроксимации точечных множеств. Теперь рассматриваем аппроксимацию функции на промежутке.

1. Ортогональность с весом.

Система функций 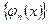,заданная на отрезке 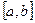называется ортогональной на этом отрезке с весом 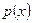, если 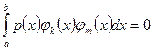при .

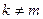Из ортогональности функции 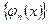с весом 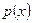следует обычная ортогональность системы .

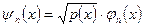Системой функций, ортогональной с весом, является полиномы Чебышева – полиномы, наименее уклоняющиеся от нуля.

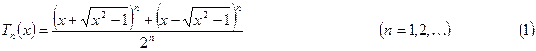
Получаем

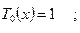
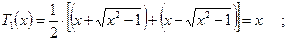
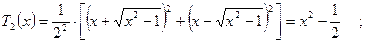
Коэффициенты при старшем числе 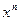всегда равны единице!

Другая форма полиномов Чебышева, рассматриваемых на отрезке .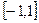

На этом отрезке можно положить 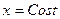; т.е. .

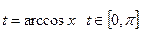Тогда 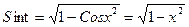, и 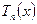примет вид

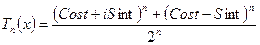при

(т.к. )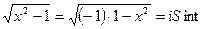

т.к. 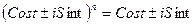, то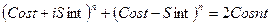

Формула 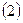неверна пр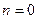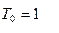и ! при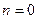

При 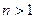из 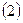получается рекуррентные формулы для вычисления полиномов Чебышева.

Т.к. ,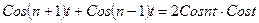

а 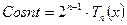- следует из 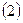,то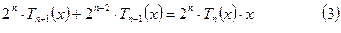

И из 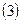следует:

Т.о. зная, что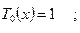

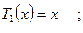
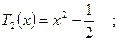
можно по 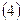вычислить последовательно все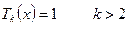

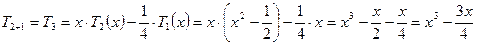и т.д.

Свойства полиномов Чебышева:

1. Полиномы Чебышева образуют на отрезке 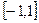ортогональную систему с весом

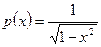, т.е. 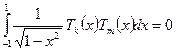при .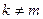

т.е. полиномы Чебышева – ортогональны с весом.

1. Все корни полинома Чебышева ненулевой степени действительны, различны и лежат на интервале .

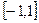1. Полином Чебышева 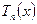при 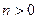на отрезке 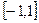имеет 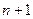экстремальных значений, равных между собой по абсолютной величине. Максимальной значение модуля полинома Чебышева 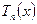при 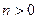на отрезке 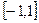равно 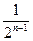, т.е. 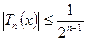при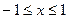

т.к. вес 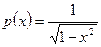возрастает при приближении к краям отрезка 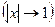,то приближения, получаемые с помощью полиномов Чебышева 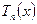, учитывают с большей степени значения аппроксимирующей функции у концов отрезка

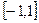
(это свойство позволяет использовать полиномы Чебышева для равномерногоприближения функции)

2. Понятие о равномерном приближении функций.

До сих пор мы рассматривали квадратичную аппроксимацию функций, при котором минимизировалось среднее квадратичное отклонение (СКО).

– СКО намножестветочек

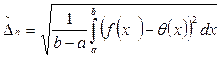– СКО при интегральной аппроксимации

(т.е. наотрезке )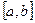

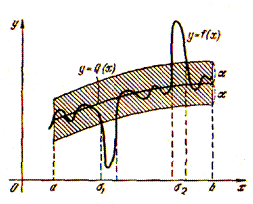
При квадратичной аппроксимации достигается выполнение неравенства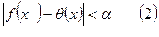

для «подавляющего большинства» значения аргумента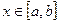

Для интервалов 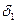и 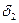условие 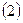может не выполняться.

При равномерномприближении выполняются более жесткие условия:

Гарантировать, чтобы на всем отрезке 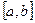отклонение функции и было меньше заданной величины.

Абсолютным отклонением на 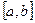обобщенного полинома 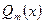от данной непрерывной функции называется число

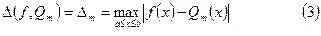
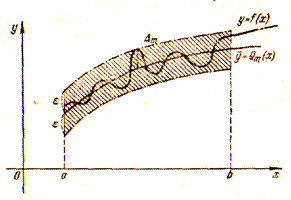Если 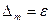для всех точек 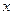на отрезке 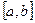, то обобщенным полином 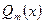на 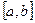равномерно приближает функцию с точностью до .

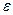Если степень 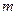полинома 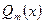фиксирована, то задача становиться таким образом: подобрать коэффициент 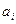полинома 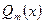так, чтобы величина

была минимальной.

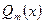Полином , дающий минимум величине 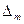, называется полиномом наилучшего приближения или полиномом, наименее отклоняющимся от на множестве .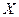

Если 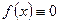, тогда полином 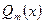, дающий минимум величине 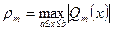называется полиномом, наименееотклоняющимсяотнуля.

Если полином 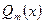ищется в виде ,

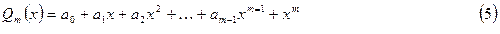(т.е. когда коэффициенты при старшей степени 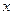равен 1), то полиномом, наименее отклоняющимся от нуля, является полином Чебышева.

Легко построить наименее отклоняющийся от нуля на данном отрезке 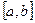полином степени m со старшим коэффициентом, равным единице.

Действительно, подстановка

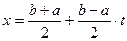
Преобразует отрезок 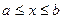в отрезок 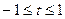, причем старший коэффициент (при 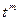) будет равен 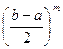. Отсюда

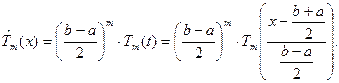(6)

Так как для полинома 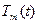отклонение от нуля равно 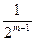, то для полинома отклонение от нуля равно

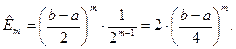(7)

Пример: С помощью полинома первой степени 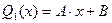наилучшим образом равномерно приблизить функцию 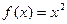на отрезке .

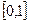Решение: Требуется определить А и В так, чтобы величина 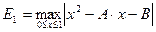была наименьшей.

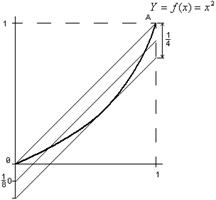
Следовательно, полином 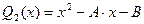наименее отклоняется от нуля на отрезке .

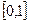Из формулы (6) получаем, полагая , .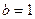

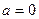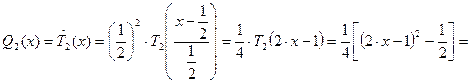
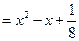, (так как )

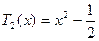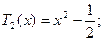
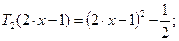
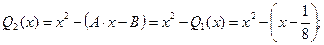
Так как .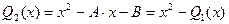

Таким образом: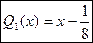

Причем 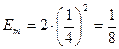(из формулы (7) )

Геометрически график - средняя параллель между секущей, проходящей через две крайние точки и , и касательной, параллельной этой секущей.

Эмпирические формулы

Пусть даны табличные значения 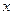и .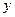

Необходимо найти аналитическую зависимость 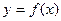. Поиск такой зависимости называют «сглаживанием» экспериментальных данных. Сглаживание можно производить, используя метод наименьших квадратов (МНК). При этом следует указать вид эмпирической формулы

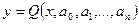(1)

Затем находится сумма квадратов отклонений

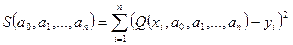(2)

и ищется ее минимум из условий 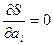, 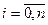(3)

В общем случае система уравнений (3) нелинейна. Ее можно решить, применяя итерационные методы.

1. Более простым методом является метод выравнивания, при котором нелинейнаязависимость (1) может быть сведена к линейной.

Пусть экспериментальные точк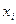и и 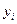не располагаются вблизи прямой. Это свидетельствует о нелинейной зависимости между 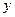и 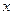. Вводятся новые переменные

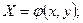
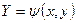. (4)

так, чтобы преобразованные экспериментальные данные ; 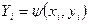менее уклонялись от прямой. Для аппроксимирующей прямой

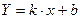(5)

Коэффициент 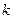и 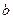можно определить из уравнений (2) и (4)

Окончательный результат получают в виде

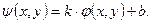(6)

Далее уравнение (6) разрешается относительно .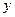

Пример: Установить вид эмпирической формулы 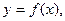используя зависимость (1) с двумя параметрами 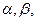и определить наилучшие значения параметров, если данные представлены таблицей

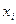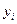	7.1	27.8	62.1

Решение: Строим график 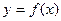. Точки не лежат на прямой.

Делаем преобразование: ; .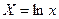

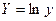Составим таблицу преобразованных данных

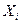	0.000	0.693	1.099	1.386	1.609
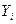	1.960	3.325	4.128	4.700	5.081

Строим график и убеждаемся, что связь между 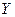и 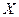почти линейная.

Составляем уравнение

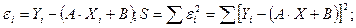
Находим 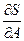и 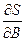, и приравниваем их нулю.

Получаем систему двух уравнений с двумя неизвестными:

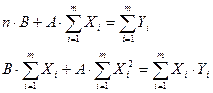
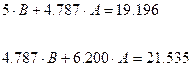
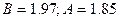
Таким образом

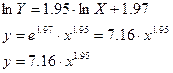
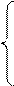Этот результат можно было бы непосредственно получить, решая задачу

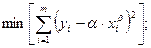
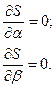
Однако, методом выравнивания задача решается проще!

1. Метод выбранных точек

Обычно применяется для нахождения начальной оценки параметров. Если связь между переменными – нелинейная, то, разлагая нелинейную зависимость в ряд по формуле Тейлора, производят линеаризацию системы, оставляя только линейные члены уравнения. Затем решение уточняется методом итераций. В качестве нулевого (начального) приближения берутся оценки параметров, найденные по методу выбранных точек.

В методе оставляют столько экспериментальных данных, сколько имеется неизвестных параметров.

Затем находится решение полученной системы!