Матрицы, действия над матрицами
ИКТИБ ИТА ЮФУ
КУРС ЛЕКЦИЙ ПО МАТЕМАТИКЕ
Глава 2 Линейная алгебра и аналитическая геометрия
Лекция 3 Матрицы, действия над ними
Что главное мы узнали на прошлых лекциях
Первые две лекции главы 1 были посвящены некоторым вопросам теории комплексных чисел и решения алгебраических уравнений.
Что мы узнаем на этой лекции
Приступая к важной главе 2, мы вначале познакомимся с новым для нас понятием в математике – матрицей. Как всегда, в математическое определение входит не только описание объекта, но и определение операций, которые можно производить над этими объектами.
Мы узнаем, что такое матрица, какие операции входят в определение матрицы, почему нельзя поделить матрицу на матрицу. Выясним, что такое квадратная, нулевая, единичная, симметричная матрица, операция транспонирования матрицы.
Матрицы, действия над матрицами
Если кратко ответить на вопрос, что такое матрица, то можно сказать, что это прямоугольная таблица чисел. Строгое определение должно содержать информацию об операциях над матрицами.
Определение 1. Прямоугольная таблица чисел, содержащая 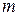 строк и
строк и 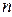 столбцов (
столбцов ( 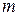 и
и 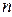 - произвольные натуральные числа), называется матрицей размерности
- произвольные натуральные числа), называется матрицей размерности 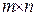 . При этом для матриц введены операции сложения, умножения на число и умножения матриц по следующим правилам:
. При этом для матриц введены операции сложения, умножения на число и умножения матриц по следующим правилам:
а) Пусть заданы две матрицы одной размерности 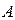 и
и 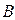 . Матрица
. Матрица 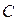 называется суммой матриц
называется суммой матриц 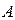 и
и 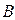 (
( 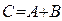 ), если она имеет ту же размерность, и при этом каждый элемент матрицы
), если она имеет ту же размерность, и при этом каждый элемент матрицы 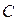 равен сумме соответствующих элементов матриц
равен сумме соответствующих элементов матриц 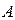 и
и 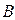 .
.
б) Пусть задана произвольная матрица 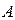 . Матрица
. Матрица 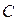 называется произведением матрицы
называется произведением матрицы 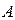 на число
на число 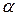 (
( 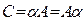 ), если она имеет ту же размерность, что и матрица
), если она имеет ту же размерность, что и матрица 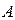 , и при этом каждый элемент матрицы
, и при этом каждый элемент матрицы 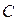 равен произведению соответствующего элемента матрицы
равен произведению соответствующего элемента матрицы 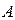 на число
на число 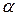 .
.
в) Пусть задана матрица 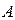 размерности
размерности 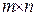 и матрица
и матрица 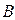 размерности
размерности 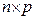 . Матрица
. Матрица 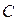 размерности
размерности 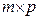 . называется произведением матрицы
. называется произведением матрицы 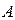 на матрицу
на матрицу 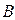 (
( 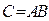 ), если элемент матрицы
), если элемент матрицы 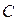 , лежащий на пересечении
, лежащий на пересечении 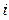 -й строки и
-й строки и 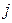 -го столбца матрицы
-го столбца матрицы 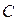 равен сумме попарных произведений соответствующих элементов
равен сумме попарных произведений соответствующих элементов 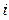 -й строки матрицы
-й строки матрицы 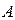 и
и 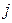 -го столбца матрицы
-го столбца матрицы 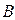 .
.
Пример 1. Даны матрицы 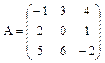 и
и 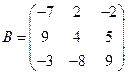 размерности
размерности 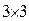 . Найдите сумму
. Найдите сумму 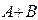 и произведение
и произведение 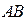 этих матриц.
этих матриц.
Решение. Нам заданы две матрицы одной размерности. Поэтому матрицы можно сложить, при сложении получится матрица той же размерности 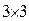 . Итак,
. Итак, 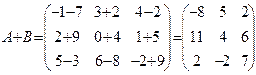 .
.
Эти две матрицы, в соответствии с определением, можно перемножить. При этом произведение матриц также является матрицей размерности 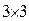 . Суть определения в том, что каждая строчка первой матрицы «умножается» на все столбцы второй матрицы. Итак, мы получаем
. Суть определения в том, что каждая строчка первой матрицы «умножается» на все столбцы второй матрицы. Итак, мы получаем 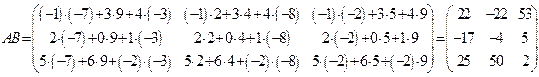 .
.
Первые две операции в определении матриц являются относительно простыми для восприятия. При сложении матриц соответствующие элементы складываются. Формально правило сложения матриц можно записать следующим образом. Пусть 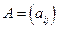 ,
, 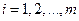 ,
, 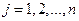 ;
; 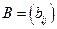 ,
, 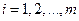 ,
, 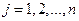 . Тогда
. Тогда 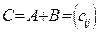 ,
, 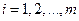 ,
, 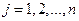 и при этом для всех допустимых значений индексов
и при этом для всех допустимых значений индексов 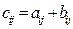 . Обратите внимание на тот факт, что сложение матриц является симметричной, по определению, операцией, поэтому справедлива формула
. Обратите внимание на тот факт, что сложение матриц является симметричной, по определению, операцией, поэтому справедлива формула 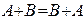 . Такая симметрия позволяет ввести операцию, обратную к операции «сложение». Эта обратная операция называется вычитанием.
. Такая симметрия позволяет ввести операцию, обратную к операции «сложение». Эта обратная операция называется вычитанием.
Разность матриц можно определить и записать следующим образом. Пусть 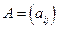 ,
, 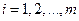 ,
, 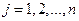 ;
; 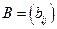 ,
, 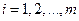 ,
, 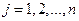 . Тогда
. Тогда 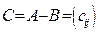 ,
, 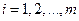 ,
, 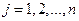 и при этом для всех допустимых значений индексов
и при этом для всех допустимых значений индексов 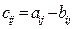 .
.
Проверьте, что в приведенном выше примере 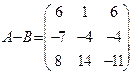 .
.
Пусть умножается матрица на число или число на матрицу. В этом случае каждый элемент матрицы умножается на это число. Эту операцию и ее результат можно записать следующим образом. Пусть 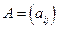 ,
, 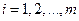 ,
, 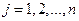 ; тогда
; тогда 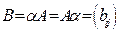 ,
, 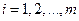 ,
, 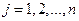 и при этом для всех допустимых значений индексов
и при этом для всех допустимых значений индексов 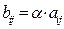 .
.
Проверьте, что в примере 1: 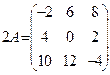 ,
, 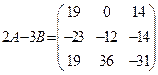 .
.
Теперь обсудим операцию умножения матриц. Алгоритм здесь следующий. В произведении 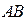 каждая строка первой матрицы умножается на каждый столбец второй матрицы. Под произведением строки на столбец понимается сумма их попарных произведений. Аналогично выглядит школьная формула для скалярного произведения векторов. Поэтому может быть употреблена такая фраза: каждая вектор-строка первой матрицы скалярно умножается на каждую вектор-столбец второй матрицы.
каждая строка первой матрицы умножается на каждый столбец второй матрицы. Под произведением строки на столбец понимается сумма их попарных произведений. Аналогично выглядит школьная формула для скалярного произведения векторов. Поэтому может быть употреблена такая фраза: каждая вектор-строка первой матрицы скалярно умножается на каждую вектор-столбец второй матрицы.
Пример 2. Даны матрицы 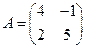 и
и 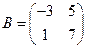 . Найдите
. Найдите 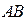 и
и 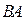 .
.
Решение. 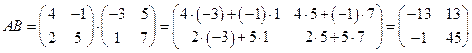
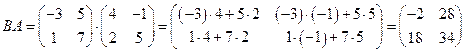 .
.
Мы видим, что 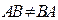 . Отсюда следует, что нельзя ввести операцию, обратную операции умножение. (Почему?!)
. Отсюда следует, что нельзя ввести операцию, обратную операции умножение. (Почему?!)
Отметим, что формула для вычисления произведения матриц не является симметричной. Поэтому, вообще говоря, как мы уже видели, 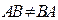 . Если в конкретной, частной ситуации выполнено условие
. Если в конкретной, частной ситуации выполнено условие 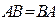 , то такие матрицы
, то такие матрицы 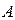 и
и 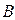 называются перестановочными. Отметим еще некоторые виды матриц. Матрица, все элементы которой равны 0, называется нулевой матрицей. Очевидно, матрица не меняется, если к ней прибавить или если от нее вычесть нулевую матрицу. Продолжим краткую формулировку некоторых определений.
называются перестановочными. Отметим еще некоторые виды матриц. Матрица, все элементы которой равны 0, называется нулевой матрицей. Очевидно, матрица не меняется, если к ней прибавить или если от нее вычесть нулевую матрицу. Продолжим краткую формулировку некоторых определений.
Если в матрице число строк равно числу столбцов, то такая матрица называется квадратной. Диагональ квадратной матрицы, идущая из левого верхнего угла в правый нижний, называется главной диагональю квадратной матрицы. Квадратная матрица называется единичной матрицей, если ее главная диагональ состоит из «1», а все остальные элементы равны 0. Если элементы квадратной матрицы симметричны относительно главной диагонали, то такая матрица называется симметричной.
Пусть строки матрицы 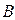 являются столбцами матрицы
являются столбцами матрицы 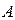 . Мы в этом случае будем говорить, что матрица
. Мы в этом случае будем говорить, что матрица 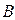 получена из матрицы
получена из матрицы 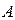 путем операции транспонирования. Очевидно, что после двукратного транспонирования мы получаем исходную матрицу.
путем операции транспонирования. Очевидно, что после двукратного транспонирования мы получаем исходную матрицу.
Итак, в общем случае матрица записывается в виде 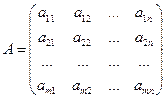 . Матрица
. Матрица 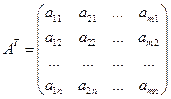 является матрицей, транспонированной к матрице
является матрицей, транспонированной к матрице 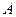 . Матрица
. Матрица 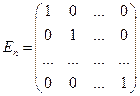 является единичной матрицей
является единичной матрицей 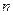 -го порядка, если в каждой строке и столбце этой матрицы
-го порядка, если в каждой строке и столбце этой матрицы 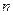 элементов. Матрицы
элементов. Матрицы 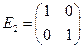 и
и 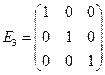 являются единичными матрицами 2-го и 3-го порядков соответственно.
являются единичными матрицами 2-го и 3-го порядков соответственно.
Проверьте, что квадратная матрица не меняется, если ее справа или слева умножить на единичную матрицу той же размерности. Этот факт можно записать в виде формулы 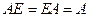 .
.
Давайте еще раз посмотрим, как перемножаются матрицы. Здесь надо помнить, что произведение матриц 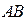 существует тогда и только тогда, когда число столбцов матрицы
существует тогда и только тогда, когда число столбцов матрицы 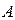 равно числу строк матрицы
равно числу строк матрицы 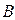 . В этом случае число строк матрицы
. В этом случае число строк матрицы 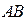 равно числу строк матрицы
равно числу строк матрицы 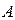 , а число столбцов матрицы
, а число столбцов матрицы 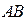 равно числу столбцов матрицы
равно числу столбцов матрицы 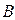 .
.
Пример 3. Даны матрицы 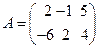 и
и 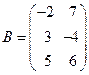 . Найдите матрицы
. Найдите матрицы 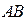 и
и 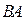 .
.
Решение. Заметим, что в данном случае матрицы можно перемножить в любом порядке. Но при этом получаются разные по порядку квадратные матрицы. Итак, 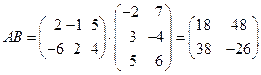 , а второе произведение равно
, а второе произведение равно 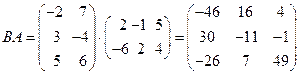 .
.
Еще раз отметим, что произведение матриц не является, вообще говоря, коммутативной операцией. В то же время остальные свойства матриц похожи на свойства действий с обычными числами. Например, если данные операции возможны, то справедливы тождества: 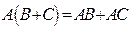 ,
, 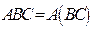 ,
, 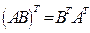 .
.
