Некоторые свойства функций
Ограниченные функции. Функция 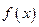 называется ограниченной сверху (снизу) в области
называется ограниченной сверху (снизу) в области 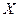 , если существует такое число
, если существует такое число 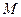 , что для всех
, что для всех 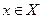 выполняется
выполняется 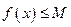 (
( 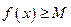 ).
).
Функция 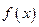 называется ограниченной в
называется ограниченной в 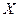 , если она ограничена и сверху и снизу, т.е. существуют такие числа
, если она ограничена и сверху и снизу, т.е. существуют такие числа 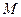 и
и 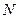 (
( 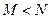 ), что для всех
), что для всех 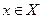 выполняется
выполняется 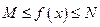 .
.
Примеры: 1. Функция 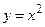 ограничена снизу на всей числовой оси, так как для всякого числа
ограничена снизу на всей числовой оси, так как для всякого числа  выполняется
выполняется  , но не ограничена сверху.
, но не ограничена сверху.
2. Функция 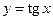 не ограничена на всей числовой оси, но ограничена на
не ограничена на всей числовой оси, но ограничена на 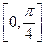 , так как
, так как 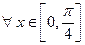 выполняется
выполняется 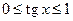 , т.е. существуют числа
, т.е. существуют числа 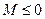 ,
, 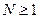 и такие, что
и такие, что 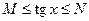 .
.
3. Функция 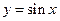 ограничена на всей числовой оси, так как для любого числа
ограничена на всей числовой оси, так как для любого числа 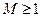 выполняется
выполняется 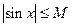 .
.
4. Функции 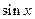 ,
, 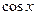 ,
, 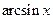 ,
, 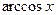 ,
, 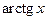 ,
, 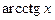 ограничены в своих областях определения.
ограничены в своих областях определения.
Монотонные функции. Пусть:
1) функция 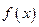 определена в D;
определена в D;
2) 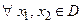 приращение функции
приращение функции 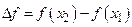 .
.
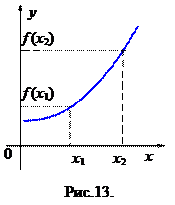
Функция 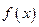 называется монотонно возрастающей (убывающей) в D в строгом смысле, если для
называется монотонно возрастающей (убывающей) в D в строгом смысле, если для 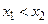 выполняется
выполняется 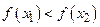 или
или 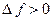 , рис.13 (
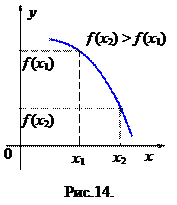
, рис.13 ( 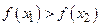 или
или 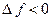 , рис. 14), и называется неубывающей (невозрастающей), если
, рис. 14), и называется неубывающей (невозрастающей), если 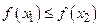 или
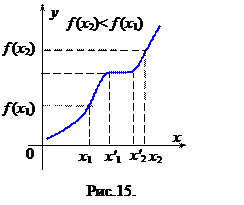
или 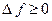 , рис.15 (
, рис.15 ( 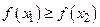 или
или 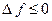 ).
).
 |  |  |
Пример. Функция 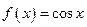 – монотонно убывающая в интервале
– монотонно убывающая в интервале 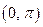 .
.
Действительно, для произвольных 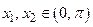 приращение функции имеет вид:
приращение функции имеет вид:
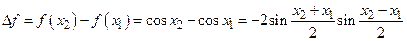 (*)
(*)
Так как 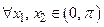 при
при 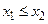 имеем
имеем 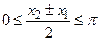 , следовательно,
, следовательно, 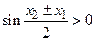 , тогда из (*) следует, что
, тогда из (*) следует, что 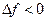 или
или 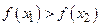 , т.е.
, т.е. 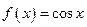 монотонно убывает в
монотонно убывает в 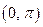 .
.
Отметим, что функции 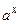 ,
, 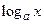 ,
, 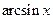 ,
, 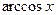 ,
, 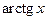 ,
, 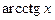 строго монотонны в своих областях определения.
строго монотонны в своих областях определения.
Если функция 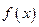 не является монотонной в области определения, но область определения можно представить в виде объединения промежутков, на каждом из которых функция является монотонной, то функция
не является монотонной в области определения, но область определения можно представить в виде объединения промежутков, на каждом из которых функция является монотонной, то функция 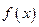 называется кусочно-монотонной.
называется кусочно-монотонной.
Пример. 1. Функция 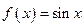 – кусочно-монотонная, так как она строго возрастает на множествах
– кусочно-монотонная, так как она строго возрастает на множествах 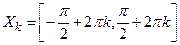 , и строго убывает на множествах
, и строго убывает на множествах 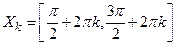 ,
, 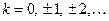 (рис. 5).
(рис. 5).
2. Функция 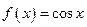 – кусочно-монотонная, так как она строго возрастает на множествах
– кусочно-монотонная, так как она строго возрастает на множествах 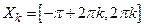 , и строго убывает на множествах
, и строго убывает на множествах 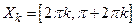
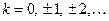 (рис. 6).
(рис. 6).
3. Функция 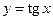 – кусочно-монотонная, так как она строго возрастает на множествах
– кусочно-монотонная, так как она строго возрастает на множествах 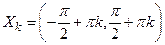 ,
, 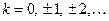 (рис. 7).
(рис. 7).
4. Функция 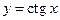 – кусочно-монотонная, так как она строго убывает на множествах
– кусочно-монотонная, так как она строго убывает на множествах 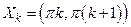 ,
, 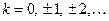 (рис. 8).
(рис. 8).
Четные и нечетные функции. Функция 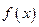 определенная в симметричном интервале
определенная в симметричном интервале 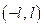 , называется четной, если
, называется четной, если 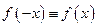 , и нечетной, если
, и нечетной, если 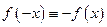 .
.
Пример. 1. 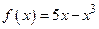 – нечетная функция, так как она определена на
– нечетная функция, так как она определена на 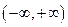 и
и
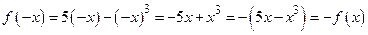 .
.
2. 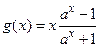 – четная функция, так как она определена на
– четная функция, так как она определена на  и
и
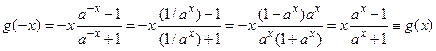 .
.
3. Докажем, что всякую функцию, определенную в 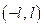 , можно представить в виде суммы четной и нечетной функций.
, можно представить в виде суммы четной и нечетной функций.
Действительно,
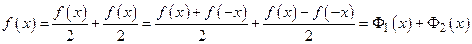 ,
,
где 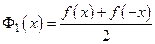 ,
, 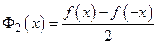 .
.
Так как 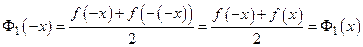 , то
, то 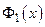 – четная функция; так как
– четная функция; так как 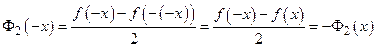 , то
, то 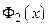 – нечетная функция. Следовательно, функция
– нечетная функция. Следовательно, функция 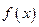 есть сумма четной функции
есть сумма четной функции 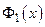 и нечетной функции
и нечетной функции 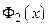 .
.
Периодические функции. Функция 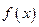 , определенная в D, называется периодической, если существует число
, определенная в D, называется периодической, если существует число 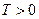 такое, что
такое, что 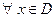 выполняется
выполняется
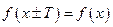 .
.
Наименьшее из Т, для которых выполняется последнее равенство, называется периодом 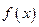 ; тогда
; тогда 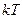 (
( 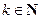 ) – период функции в широком смысле слова.
) – период функции в широком смысле слова.
Пример. Найти, если существует, период функции 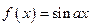 (
( 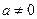 ).
).
Решение. Функция определена 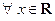 . По определению
. По определению 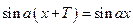 или
или 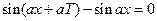 – уравнение для определения
– уравнение для определения 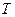 ; преобразуем его:
; преобразуем его: 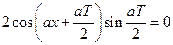 . Так как
. Так как  – любое из
– любое из 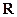 , то последнее уравнение выполняется, если
, то последнее уравнение выполняется, если 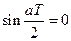 , отсюда
, отсюда 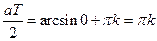 , т.е.
, т.е. 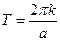 . Наименьшее положительное (отличное от нуля)
. Наименьшее положительное (отличное от нуля) 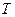 получим при
получим при 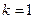 . Итак, функция
. Итак, функция 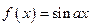 – периодическая с периодом
– периодическая с периодом 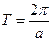 .
.
Замечание. Функции 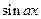 ,
, 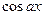 имеют период
имеют период 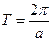 , функции
, функции 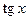 ,
, 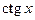 – период
– период 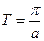 .
.
Теорема. Если функция 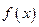 , определенная в
, определенная в 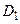 , имеет период
, имеет период 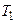 , а функция
, а функция 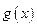 , определенная в
, определенная в 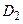 , – период
, – период 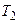 , то
, то
1) функция 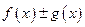 , определенная в
, определенная в 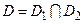 будет периодической с периодом
будет периодической с периодом 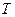 , если отношение
, если отношение 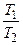 – рациональное число;
– рациональное число;
2) период 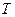 – наименьшее общее кратное чисел,
– наименьшее общее кратное чисел, 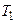 и
и 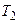 .
.
Доказательство. 1) По определению
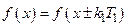 ,
, 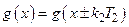 ,
,
где 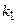 ,
, 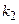 – целые.
– целые.
Пусть 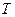 кратное чисел
кратное чисел 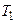 и
и 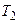 , тогда
, тогда 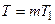 и
и 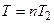 , где
, где 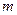 и
и 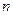 – целые числа, тогда
– целые числа, тогда 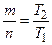 – рациональное число.
– рациональное число.
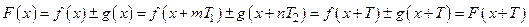 , т.е. функция
, т.е. функция  – периодическая с периодом
– периодическая с периодом  в широком смысле. Если
в широком смысле. Если  – наименьшее общее кратное чисел
– наименьшее общее кратное чисел 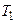 и
и 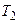 , то
, то 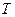 – период функции
– период функции 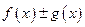 .
.
Пример. Будет ли периодической функция 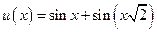 ?
?
Решение. Функции 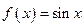 и
и 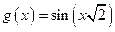 определены
определены 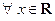 и имеют периоды
и имеют периоды 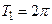 и
и 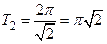 соответственно. Тогда
соответственно. Тогда 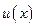 определена
определена  . Так как
. Так как 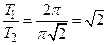 – иррациональное число, то функция
– иррациональное число, то функция 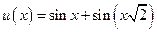 – непериодическая.
– непериодическая.
Обратные функции
 Рассмотрим примеры. Основная элементарная функция
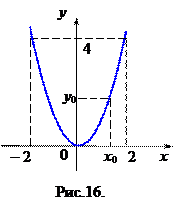
Рассмотрим примеры. Основная элементарная функция 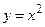 , определенная на
, определенная на 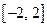 , каждому числу
, каждому числу 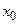 из множества
из множества 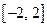 ставит в соответствие единственное число
ставит в соответствие единственное число 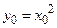 из отрезка
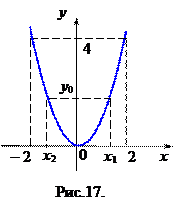
из отрезка 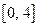 (рис.16). Возникает вопрос, найдется ли для конкретного числа
(рис.16). Возникает вопрос, найдется ли для конкретного числа 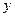 из отрезка
из отрезка 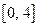 значение
значение  , такое, что
, такое, что 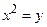 . Непосредственной проверкой убеждаемся, что такими числами будут
. Непосредственной проверкой убеждаемся, что такими числами будут 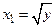 и
и 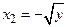 (рис. 17).
(рис. 17).
Действительно, 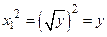 и
и 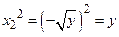 . Так для
. Так для 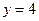 находим
находим 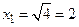 и
и 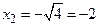 .
.
Таким образом, всякому числу 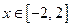 функция
функция 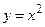 ставит в соответствие единственное число
ставит в соответствие единственное число 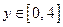 , но для всякого числа
, но для всякого числа 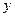 , отличного от нуля из отрезка
, отличного от нуля из отрезка 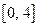 можно указать, по крайней мере, две функции
можно указать, по крайней мере, две функции 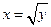 и
и 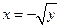 , которые переводят одну и ту же точку из
, которые переводят одну и ту же точку из 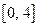 в две разные точки из множества
в две разные точки из множества 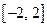 . Функция
. Функция 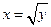 каждой точке
каждой точке 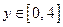 ставит в соответствие единственную точку
ставит в соответствие единственную точку 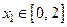 , а функция
, а функция 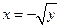 каждой точке
каждой точке 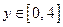 ставит в соответствие единственную точку
ставит в соответствие единственную точку 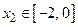 . Таким образом, не существует единственной основной элементарной функции, которая переводила бы все точки из множества
. Таким образом, не существует единственной основной элементарной функции, которая переводила бы все точки из множества 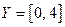 во все точки множества
во все точки множества 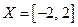 .
.
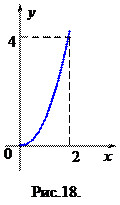 Рассмотрим теперь функцию
Рассмотрим теперь функцию 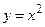 ,
, 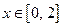 (рис. 18), которая отличается от выше рассмотренной функции только областью определения. Эта функция каждому числу
(рис. 18), которая отличается от выше рассмотренной функции только областью определения. Эта функция каждому числу 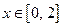 ставит в соответствие единственное число
ставит в соответствие единственное число 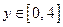 . Функция
. Функция 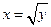 каждому
каждому 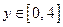 ставит в соответствие единственное число
ставит в соответствие единственное число 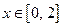 . Таким образом, между числовыми множествами
. Таким образом, между числовыми множествами 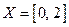 и
и 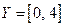 установлено взаимно однозначное соответствие и, кроме того,
установлено взаимно однозначное соответствие и, кроме того, 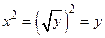 . Функция
. Функция 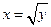 в таком случае называется обратной для функции
в таком случае называется обратной для функции 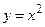 , а функция
, а функция 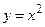 , в свою очередь, называется обратной для функции
, в свою очередь, называется обратной для функции 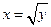 .
.
Возникает вопрос, в каких случаях для функции 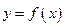 существует обратная функция? Ответ дает следующая теорема (приведем ее без доказательства).
существует обратная функция? Ответ дает следующая теорема (приведем ее без доказательства).
Теорема.Если непрерывная функция 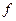 строго монотонна в области
строго монотонна в области 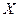 и имеет область значений
и имеет область значений 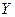 , то для нее существует однозначная обратная функция
, то для нее существует однозначная обратная функция 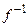 , определенная на
, определенная на 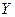 и с областью значений
и с областью значений 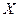 .
.
Замечание. Предполагается, что понятие непрерывной функции знакомо из школьного курса математики, хотя бы как функции, график которой – сплошная линия, т.е. его можно нарисовать одним росчерком (не отрывая карандаша от бумаги). Чуть позже дадим строгое определение непрерывной функции.
Пример. Показательная функция 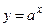 является непрерывной и строго монотонной (строго возрастающей при
является непрерывной и строго монотонной (строго возрастающей при 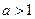 и строго убывающей при
и строго убывающей при 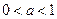 ), т.е. удовлетворяет условиям теоремы о существовании обратной функции. Такой функцией является функция
), т.е. удовлетворяет условиям теоремы о существовании обратной функции. Такой функцией является функция 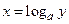 (
( 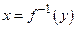 ).
).
Так как ранее условились обозначать функцию символом 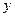 , а аргумент символом
, а аргумент символом  , то в обратной функции
, то в обратной функции 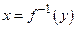 символы
символы  и
и 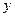 меняем местами и имеем обратную функцию в виде
меняем местами и имеем обратную функцию в виде 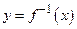 .
.
Тогда функция 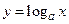 есть обратная для функции
есть обратная для функции 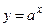 , а функция
, а функция 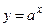 есть обратная для функции
есть обратная для функции 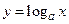 , и, таким образом,
, и, таким образом, 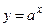 и
и 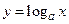 – взаимно обратные функции.
– взаимно обратные функции.
Обратные тригонометрические функции 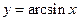 ,
, 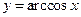 ,
, 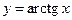 ,
, 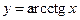 ввели как обратные соответствующим тригонометрическим функциям (этот факт зафиксирован уже в самом названии функций), а затем поменяли местами символы
ввели как обратные соответствующим тригонометрическим функциям (этот факт зафиксирован уже в самом названии функций), а затем поменяли местами символы  и
и 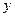 .
.
Так функция 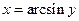 есть обратная для строго монотонной функции
есть обратная для строго монотонной функции 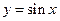 с областью определения
с областью определения 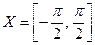 и множеством значений
и множеством значений 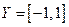 ; функция
; функция 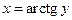 есть обратная функция для строго монотонной функции
есть обратная функция для строго монотонной функции 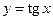 с областью определения
с областью определения 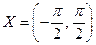 и множеством значений
и множеством значений 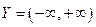 .
.
 Для монотонных функций заданных аналитически
Для монотонных функций заданных аналитически 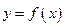 обратную функцию можно получить, выразив
обратную функцию можно получить, выразив  через
через 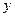 (для этого необходимо найти
(для этого необходимо найти  из уравнения
из уравнения 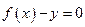 ).
).
Для кусочно-монотонных функций обратную функцию находят на каждом интервале монотонности.
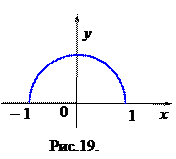
Пример. 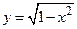 ,
, 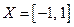 ,
, 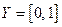 . Функция представлена графиком (рис.19). На отрезке
. Функция представлена графиком (рис.19). На отрезке 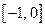 функция строго возрастает, следовательно, существует обратная к ней функция, которую найдем последовательно выполняя преобразования:
функция строго возрастает, следовательно, существует обратная к ней функция, которую найдем последовательно выполняя преобразования:
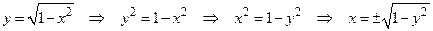 .
.
Так как 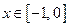 , то искомой обратной функцией будет
, то искомой обратной функцией будет 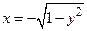 с областью определения
с областью определения 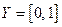 и множеством значений
и множеством значений 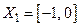 .
.
Для убывающей на отрезке 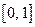 функции
функции 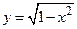 получим (повторив преобразования) обратную функцию
получим (повторив преобразования) обратную функцию 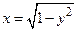 с областью определения
с областью определения 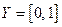 и множеством значений
и множеством значений 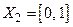 .
.
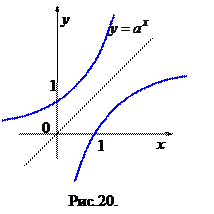 Отметим, что графики взаимно обратных функций
Отметим, что графики взаимно обратных функций 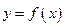 и
и 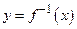 симметричны относительно прямой
симметричны относительно прямой 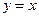 (биссектрисы первого и третьего координатных углов). Действительно, точка
(биссектрисы первого и третьего координатных углов). Действительно, точка 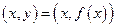 графика функции
графика функции 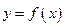 симметрична относительно прямой
симметрична относительно прямой 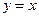 точке
точке 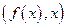 . Если обозначить
. Если обозначить 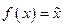 , то
, то 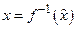 и точка
и точка 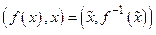 является точкой графика функции
является точкой графика функции 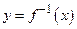 при значении аргумента
при значении аргумента 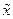 .
.
Например, графики функций 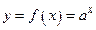 и
и 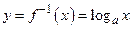 симметричны относительно прямой
симметричны относительно прямой 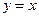 (рис. 20).
(рис. 20).
Аналогично, графики попарно взаимно обратных функций 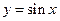 и
и 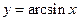 ,
, 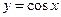 и
и 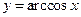 ,
, 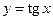 и
и 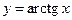 ,
, 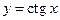 и
и 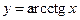 тоже симметричны относительно прямой
тоже симметричны относительно прямой 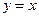 .
.
Элементарные функции
Элементарной функцией называется всякая функция, которая может быть явным образом задана с помощью формулы, содержащей лишь конечное число арифметических операций (сложения, вычитания, умножения, деления) и композиций над основными элементарными функциями.
