Обобщённый закон Ома. Закон Ома для участка цепи

Закон Ома для участка цепи.

больше .Тогда закон Ома для данного участка цепи будет иметь вид:

Обобщенный закон Ома.

больше .

1) (источник ЭДС – генератор)

2) (источник ЭДС – двигатель)

Закон Ома для цепи, содержащей источник ЭДС (обобщенный закон Ома):

I=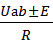

Первый и второй законы Кирхгофа. Расчёт электричес-кой цепи по законам Кирхгофа ( на примере электрической цепи).

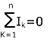Первый закон Кирхгофа - алгебраическая сумма всех токов, сходящихся в узле равна нулю.

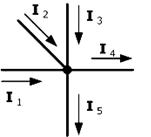(Токи, направленные к узлу, условно принимаются отрицательными, а направленные от него -положительными). На

-I₁-I₂-I₃+I₄+I₅=0

I₁+I₂+I₃=I₄+I₅

Второй закон Кирхгофа - Вдоль замкнутого контура алгебраическая сумма падений напряжений в отдельных элементах контура равна алгебраической сумме ЭДС, входящих в этот контур (или 0, если контур не содержит ЭДС)

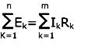
Пример расчета цепи, основанного законах Кирхгофа:

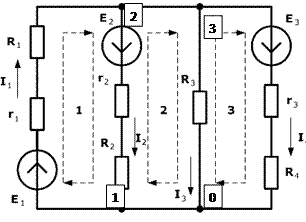
· Число уравнений по первому закону Кирхгофа равно числу узлов минус 1

1) I₁-I₂₌₀

2) -I₁+I₂₌₀

3) -I₁₊ I₃+I₄₌₀

· Число уравнений по второму закону Кирхгофа равно числу независимых контуров:

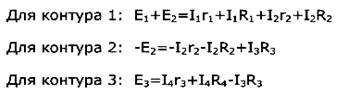
Последовательное, параллельное и смешанное соединение элементов.

А) Последовательное соединение – это такое соединение, при котором через все элементы протекает один и тот же ток I=I₁=I₂=I₃ , при этом U=U₁+U₂+U₃= I₁R₁+I₂R₂+I₃R₃=I*(R₁+R₂+R₃). Где Rэкв= R₁+R₂+R₃

I*Rэкв=U

При последовательном соединении все сопротивления можно заменить одним эквивалентным.

Б) Параллельное соединение – при нем все элементы присоединяются к одной паре узлов, т.е. находятся под одним напряжением. I₁=U₁/R₁; I₂=U₂/R₂; I₃=U₃/R , тогда I=I₁+I₂+I₃. Тогда U/Rэкв=U₁/R₁+U₂/R₂+U₃/R₃ а значит 1/Rэкв=1/ R₁+1/R₂+1/ R₃, а I=U/Rэкв

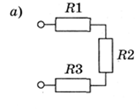
В) Смешанное соединение – такое соединение элементов, которое содержит последовательно и параллельно соединенные элементы. Rэкв=R₁+R₂+R₆+R₁R₂R₃/(R₁R₂+R₂R₃+R₁R₃)

Метод эквивалентных преобразований с одним источником.

Дано: R1, R2, R3, R4, R5,R6, E Найти: I.

R456=R4+R5+R6; R12=R1+R2; тогда преобразуем данную схему (рис.1) в эквивалентную (рис.2) с учетом этих преобразований.

R3456=(R3*R456)/(R3+R456). Исходя из этого преобразования преобразуем схему (рис.2) в эквивалентную (рис.3). I1=E/(R12+R3456)

I способ. Uab=E-I1R12; I2=Uab/R3; I3=Uab/R456.

II способ. В нем используется формула «разброса». I2=I1*R456/(R3+R456); I3=I1*R3/(R3+R456)

В случае, когда в электрической цепи имеется источник тока, то для определения тока, то для определения тока в ветвях можно использовать только формулу «разброса».

Рис.1

Рис.2

Метод контурных токов

уравнения метода контурных токов составляются только по второму закону Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи графа . Первый закон Кирхгофа выполняется автоматически. Контуры можно выбирать произвольно, лишь бы их число было равно и чтобы каждый новый контур содержал хотя бы одну ветвь, не входящую в предыдущие. Такие контуры называются независимыми.

Направления истинных и контурных токов выбираются произвольно. Выбор положительных направлений перед началом расчета может не определять действительные направления токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его истинное направление противоположно.

При составлении уравнений необходимо помнить следующее:

· - сумма сопротивлений, входящих в i-й контур;

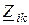· - сумма сопротивлений, общих для i-го и k-гоконтуров, причем ;

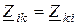· члены на главной диагонали всегда пишутся со знаком “+”;

· знак “+” перед остальными членами ставится в случае, если через общее сопротивление 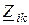i-й и k- й контурные токи проходят в одном направлении, в противном случае ставится знак “-”;

· если i-й и k- й контуры не имеют общих сопротивлений, то ;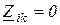

· в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением контурного тока, и “-”, если не совпадает.

Пример расчета цепи методом контурных токов

Пусть имеем схему по рис. 3.

Выразим токи ветвей через контурные токи:

;

; ;

; .

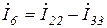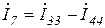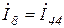Обойдя контур aeda, по второму закону Кирхгофа имеем:

.Поскольку:

То:

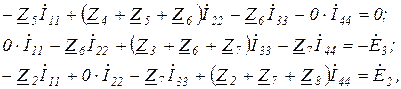Таким образом, получили уравнение для первого контура относительно контурных токов. Аналогично можно составить уравнения для второго, третьего и четвертого контуров

Совместно с первым решить их относительно контурных токов и затем по уравнениям, связывающим контурные токи и токи ветвей, найти последние.