Колебательный контур. Добротность контура
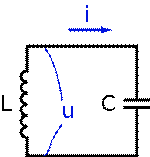
Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).
Пусть конденсатор ёмкостью C заряжен до напряжения 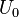 . Энергия, запасённая в конденсаторе составляет:
. Энергия, запасённая в конденсаторе составляет:
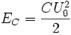
При соединении конденсатора с катушкой индуктивности, в цепи потечёт ток 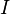 , что вызовет в катушке ЭДС самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности) в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.
, что вызовет в катушке ЭДС самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности) в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.
Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора 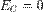 . Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна
. Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна
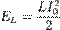 , где
, где 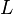 — индуктивность катушки,
— индуктивность катушки, 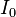 — максимальное значение тока.
— максимальное значение тока.
После этого начнётся перезарядка конденсатора, то есть заряд конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор, в этом случае, снова будет заряжен до напряжения 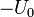 .
.
В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.
В общем, описанные выше процессы в параллельном колебательном контуре называются резонанс токов, что означает, что через индуктивностьи ёмкость протекают токи, больше тока проходящего через весь контур, причем эти токи больше в определённое число раз, которое называется добротностью. Эти большие токи не покидают пределов контура, так как они противофазны и сами себя компенсируют. Стоит также заметить, что сопротивление параллельного колебательного контура на резонансной частоте стремится к бесконечности (в отличие от последовательного колебательного контура, сопротивление которого на резонансной частоте стремится к нулю), а это делает его незаменимым фильтром.
Стоит заметить, что помимо простого колебательного контура, есть ещё колебательные контуры первого, второго и третьего рода, что учитывают потери и имеют другие особенности.
Резонансная частота контура определяется так называемой формулой Томсона:
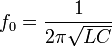
Напряжение, возникающее в катушке при изменении протекающего тока равно
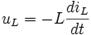
Аналогично для тока, вызванного изменением напряжения на конденсаторе:
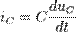
Поскольку всё возникающее в катушке напряжение падает на конденсаторе, то 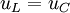 , а ток, вызванный конденсатором проходит через катушку, то
, а ток, вызванный конденсатором проходит через катушку, то 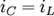 . Дифференцируя одно из уравнений и подставляя результат в другое, получаем:
. Дифференцируя одно из уравнений и подставляя результат в другое, получаем:
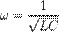
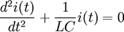
Это уравнение гармонического осциллятора с циклической частотой:
Решением такого уравнения является:
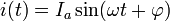
Добротносью контура (истинная) – это отношение полной проводимости к величине активной проводимости:
Q= Yв/G= 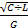 . Добротность контура тем выше, чем меньше величина проводимости или больше величина сопротивлений.
. Добротность контура тем выше, чем меньше величина проводимости или больше величина сопротивлений.
39) 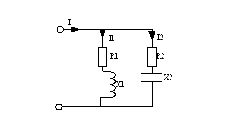 Параллельное соединение R-L-C элементов. Треугольник токов и проводимостей.
Параллельное соединение R-L-C элементов. Треугольник токов и проводимостей.
Имеем цепь:
Zэкв1=R1+jX1; Zэкв2=R2-jX2; I1=U/Zэкв1; I2=U/Zэкв2; I=I1+I2=U(1/ Zэкв1+ Zэкв2)=U(Yэкв1+ Yэкв2)=UY
Yэкв1=1/(R1+jX1)=(R1+jX)/(R21+X21)=R1/( R21+X21)-jX1/( R21+X21)=G - jBL,
где G=R1/ (R21+X21), BL=X1/ (R21+X21)
Если в ветви вместо L имеется С то в этом случае составляющие реактивной проводимости записываются со знаком «+»: Yэкв2= G + jBс
Треугольник проводимостей:
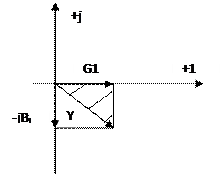
G1=Ycosα; BL=Ysinα; Y= 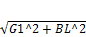 *e-jarctgBL/G1
*e-jarctgBL/G1
Iα=G1*U; Ip=BL*U
Треугольник токов

I=(I2a+I2p)0.5
Ì=(I2a+I2p)0.5e-jarctgIp/Ia
