Численные методы решения обыкновенных дифференциальных уравнений

Метод Эйлера.

В основе метода Эйлера (метод ломаных) лежит идея графического построения решения дифференциальных уравнений, однако этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.

Пусть дано дифференциальное уравнение:

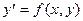
с начальными условиями:

.

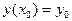Выбрав достаточно малый шаг h, строится система равноотстоящих точек .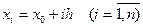

В методе Эйлера приближенные значения 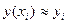вычисляются последовательно по формулам:

.

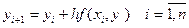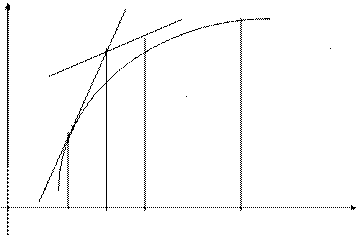
При этом искомая интегральная кривая 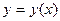, проходящая через точку 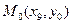, заменяется ломанной 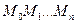с вершинами 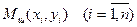; каждое звено 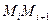этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения 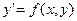, которая проходит через точку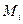

y

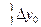
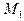
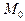
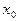
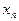
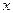
Пример

Пусть дано дифференциальное уравнение:

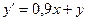
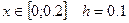
с начальными условиями:

.

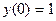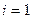
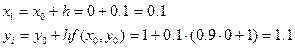
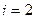
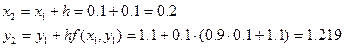
Решение ОДУ имеет вид:

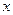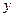0.0	1.000
0.1	1.100
0.2	1.219

Особенности метода Эйлера.

Метод очень прост в реализации, но обладает малой точностью, поскольку погрешность каждого нового шага систематически возрастает. Существует модификации метода, повышающие его точность, - методы Эйлера-Коши – первая и вторая улучшенные формулы.

Первая улучшенная формула Эйлера

Пусть дано дифференциальное уравнение:

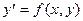
с начальными условиями:

.

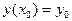Решение в каждой точке 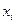определяется по формуле:

,

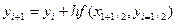где

.

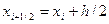
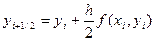Геометрически это означает, что отрезок ломанная между точками 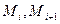заменяется на два отрезка 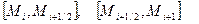. Направление первого отрезка совпадает с направлением интегральной кривой в точке

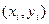, а направление второго отрезка определяется направлением, интегральной кривой в вспомогательной точке .

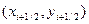Пример.

Пусть дано дифференциальное уравнение:

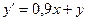
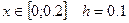
с начальными условиями:

.

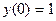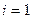
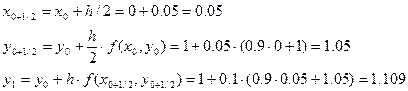
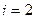
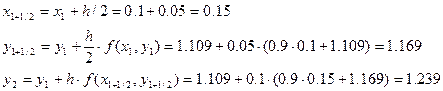
Решение ОДУ имеет вид:

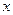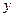0.0	1.000
0.1	1.109
0.2	1.239

Вторая улучшенная формула Эйлера

Пусть дано дифференциальное уравнение:

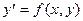
с начальными условиями:

.

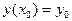Решение в каждой точке 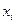определяется по формуле:

,

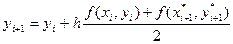где

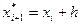
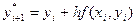
Геометрически это означает, что определяется направление интегральной кривой в исходной точке 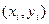и во вспомогательной точке 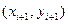, а в качестве окончательного направления ломаной берется среднее этих направлений.

Пример.

Пусть дано дифференциальное уравнение:

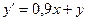
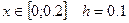
с начальными условиями:

.

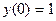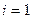
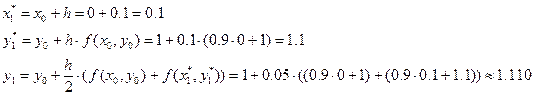
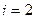
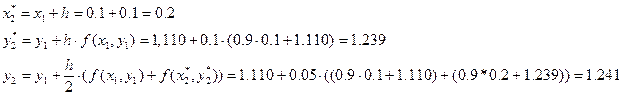Решение ОДУ имеет вид:

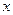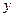0.0	1.000
0.1	1.110
0.2	1.241

Метод Рунге-Кутта.

Метод Эйлера относится к семейству методов Рунге-Кутта.

Метод Рунге-Кутта 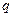-го порядка имеет вид:

,

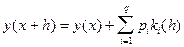где при фиксированных значениях некоторых параметров:

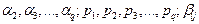
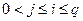
последовательно вычисляются:

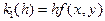
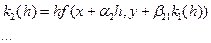
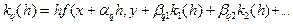
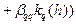
Наибольшее применение на практике получил метод Руте-Кутта 4-го порядка:

,

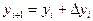где

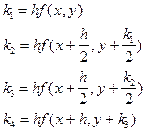
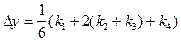
Метод Рунге-Кутта имеет ряд важнейших достоинств:

1) высокая точность

2) явная схема вычислений 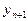за определенное количество шагов и по определенным формулам.

3) возможен переменный шаг, т.е. можно сменить шаг, где функция быстро меняется.

4) легко оформляется.

Пусть дано дифференциальное уравнение:

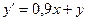
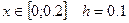
с начальными условиями:

.

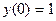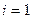
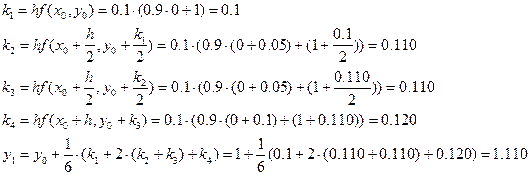
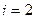
Решение ОДУ имеет вид:

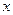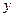0.0	1.000
0.1	1.110
0.2	1.241