Произведение равно нулю , когда хотя бы один из сомножителей равен нулю

Приравняем к нулю каждый сомножитель, получим:

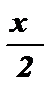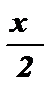sin = 0; = pk , х = 2pk , k Î Z .

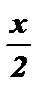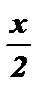cos - sin = 0;

Полученное тригонометрическое уравнение является однородным первой степени относительно sin 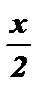и cos .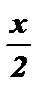

Разделим обе части этого уравнения на cos 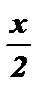¹ 0, получим:

1 - tg 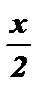= 0; tg 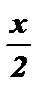= 1; 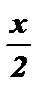= arctg 1 + pk ; 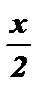= 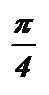+ pk ; х = 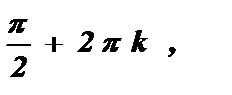k Î Z

Ответ: х = 2pk , х = 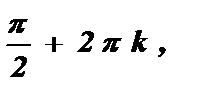k Î Z .

Упражнения:

№1. Решить уравнения:

1) sin 2x = 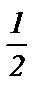; 6) cos 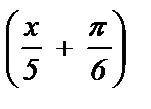= -1 ; 11) ctg 3x = ;

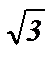2) sin 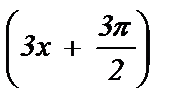= 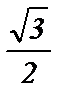; 7) cos 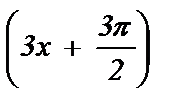= 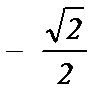; 12) ctg 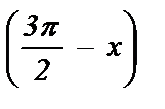= -1 ;

3) sin 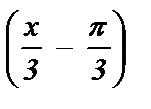= 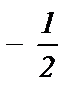; 8) cos 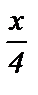= 0; 13) tg = ;

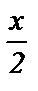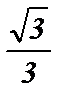4) 2 sin 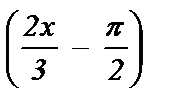= -1 ; 9) 3 cos x = 2; 14) tg 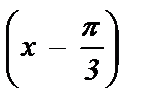= 3;

5) sin 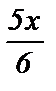= 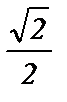; 10) cos 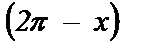= 1; 15) ctg = .

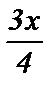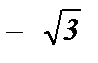№2. Решить уравнения:

1) 4 sin ² x + 11 sin x - 3 = 0; 11) 3 sin ² x + sin x cos x = 2 cos ² x;

2) tg ² x + 2 tg x - 3 = 0; 12) 9 sin x cos x - 7 cos ² x = 2 sin ² x;

3) ctg ² 2x - tg 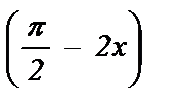- 2 = 0; 13) 4 sin ² x = 3 + sin 2x;

4) 2 sin ² x - 5 cos x +1 = 0; 14) cos 2x = 2 cos x - 1;

5) 5 sin ² 2x + 6 cos 2x - 6 = 0; 15) sin x - cos x = 0;

6) cos ² x + 3 sin x = 3; 16) sin 3x - 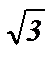cos 3x = 0;

7) 4 cos ² 3x - 3 = 0; 17) sin ⁴ 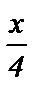- cos ⁴ = ;

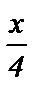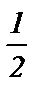8) 3 sin ² x - cos ² x = 1; 18) 1 - cos x = 2 sin ;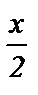

9) 2 tg ² 5x + 3 tg 5x - 2 = 0; 19) sin 4x + sin ² 2x = 0;

10) sin ⁴ x - cos ⁴ x = 0,5; 20) 4sin x + 3cos x = - 3.

№3. Решить уравнения:

1) (sin 2x - 1) tg x = 0; 11) cos 4x cos 2x = cos 5x cos x;

2) 2 cos x ctg 3x = ctg 3x; 12) sin 6x cos 2x = sin 5x cos 3x;

3) sin 3x + sin x = 0; 13) cos 2x cos 3x = sin 6x sin x;

4) cos (3x - 2p) + sin 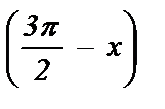= 0; 14) tg 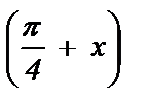+ tg x + 2 = 0;

5) cos 2x - cos x = 0; 15) tg x - 2 ctg x = 1;

6) cos 3x = sin x; 16) 4 sin 2x - 3 cos 2x = 3;

7) tg x = tg 2x; 17) 1 - sin ² x + sin ² 2x = 0;

8) tg 2x - 3 tg x = 0; 18) tg ⁴ x - tg ² x - 12 = 0;

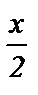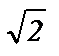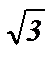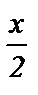9) 3 cos x + 5 sin = - 1; 19) (2 sin 3x + )(tg x - ) cos = 0;

10) tg 5x = tg 3x; 20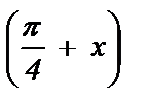) tg + tg 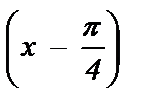= 2 ctg x .

21. Простейшие тригонометрические неравенства.

sin x £ a

sin x £ a Û - p - arcsin a + 2pk £ x £ arcsin a + 2pk , k Î Z .

sin x ³ a

sin x ³ a Û arcsin a + 2pk £ x £ p - arcsin a + 2pk , k Î Z .

cos x £ a

cos x £ a Û arccos a + 2pk £ x £ 2p - arccos a + 2pk , k Î Z .

cos x ³ a

cos x ³ a Û - arccos a + 2pk £ x £ arccos a + 2pk , k Î Z .

tg x £ a Û 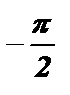+ pk < x £ arctg a + pk , k Î Z .

tg x ³ a Û arctg a + pk £ x < 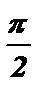+ pk , k Î Z .

ctg x £ a Û arcctg a + pk £ x < p + pk , k Î Z .

ctg x ³ a Û pk < x £ arcctg a + pk , k Î Z .

Пример №1: Решить неравенство: sin x ³ .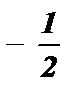

Решение:

sin x ³ a Û arcsin a + 2pk £ x £ p - arcsin a + 2pk , k Î Z .

arcsin 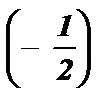+ 2pk £ x £ p - arcsin 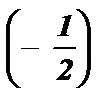+ 2pk , k Î Z ;

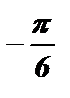+ 2pk £ x £ p - 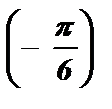+ 2pk , k Î Z ;

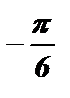+ 2pk £ x £ 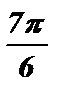+ 2pk , k Î Z .

Ответ: 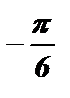+ 2pk £ x £ 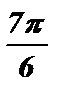+ 2pk , k Î Z .

Пример №2: Решить неравенство: cos 2x ³ .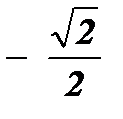

Решение:

cos x ³ a Û - arccos a + 2pk £ x £ arccos a + 2pk , k Î Z .

- arccos 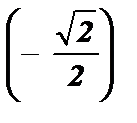+ 2pk £ 2x £ arccos 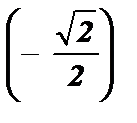+ 2pk , k Î Z ;

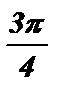- + 2pk £ 2x £ 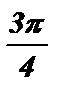+ 2pk , k Î Z ;

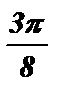- + 2pk £ x £ 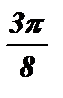+ 2pk , k Î Z .

Ответ: - 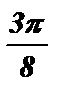+ 2pk £ x £ 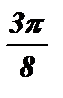+ 2pk , k Î Z .

Пример №3: Решить неравенство: 3 tg < .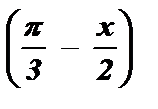

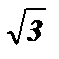Решение:

Разделим обе части неравенства на 3: tg < ;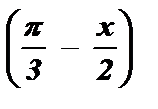

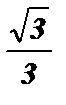Воспользуемся нечетностью тангенса:

tg 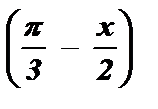= - tg 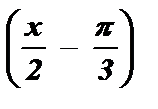; - tg < ;

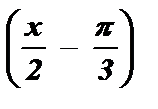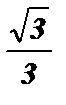Разделим обе части неравенства на - 1: tg > - ;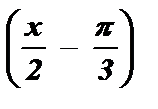

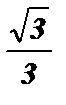Воспользуемся формулой решений неравенства tg x ³ a :

arctg a + pk £ x < 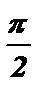+ pk , k Î Z .

arctg 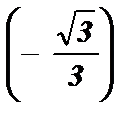+ pk £ 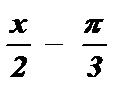< 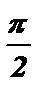+ pk , k Î Z;

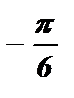+ pk £ 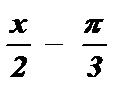< 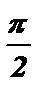+ pk , k Î Z;

Прибавим ко всем частям неравенства :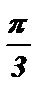

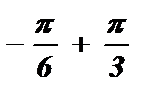+ pk £ 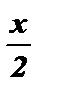< 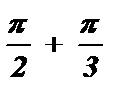+ pk , k Î Z;

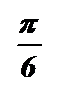+ pk £ 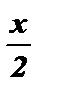< 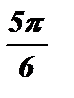+ pk , k Î Z;

Умножим все части неравенства на 2:

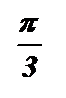+ 2pk £ х < 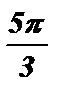+ 2pk , k Î Z;

Ответ: 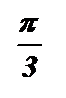+ 2pk £ х < 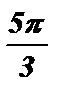+ 2pk , k Î Z;

Формулы тригонометрии

Основные тригонометрические тождества

sin ²a + cos ²a = 1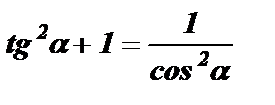

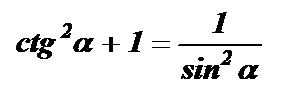
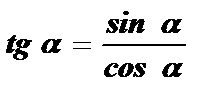
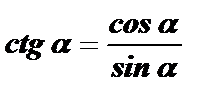tg a · сtg a = 1