Раздел 2. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Аналитическая геометрия – раздел геометрии, в котором простейшие геометрические образы (прямые, плоскости, линии второго порядка, поверхности) исследуются средствами алгебры на основе метода координат.
Тема 1. Системы координат. Простейшие задачи
Аналитической геометрии
Основные задачи аналитической геометрии
Расстояние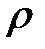 
между точками 
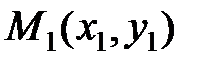и 
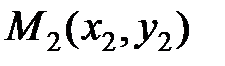находится по формуле:
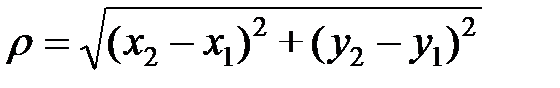. (2.1)
Деление отрезка в заданном отношении. Рассмотрим две различные точк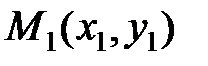и 
и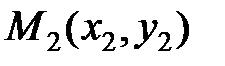 
. Если точка 
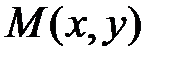делит отрезок 
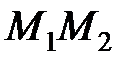, в отношении λ, считая от точки 
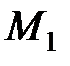т.е. λ= 
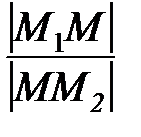, то ее координаты определяются формулами:
, 
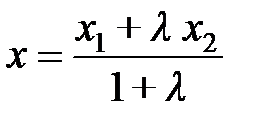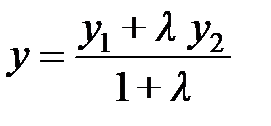, (2.2)
в частности, если точка 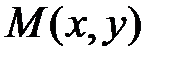является серединой отрезка 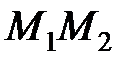, т.е. λ=1, из (2.2) получим формулы деления отрезка пополам:
, 
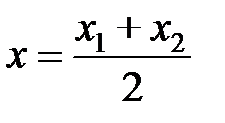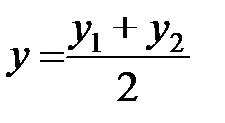. (2.3)
Тема 2. Общие понятия уравнения линии на плоскости.
Прямая на плоскости
Уравнением линии на плоскости, относительно выбранной системы координат, называется такое уравнение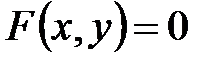 
, которому удовлетворяют координаты любой точки данной линии и не удовлетворяют координаты точек, не лежащих на этой линии. В уравнении 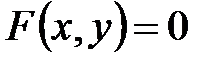координаты 
, 
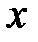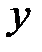называют текущими координатами, или координатами текущей точки.
Уравнения прямой на плоскости задаются алгебраическими уравнениями первой степени относительно декартовых координат:
1) Общее уравнение прямой:
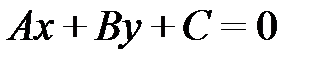, где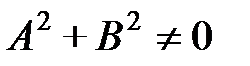 
; (2.4)
2) Уравнение прямой, проходящей через две заданные точк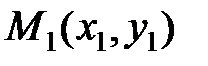и и 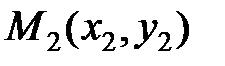, имеет вид:
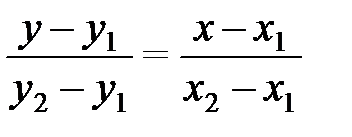; (2.5)
Замечание. Если знаменатель одной из дробей в (2.5) равен нулю, то для записи уравнения прямой необходимо соответствующий числитель приравнять к нулю, т.е. получим прямую параллельную одной из координатных осей вида: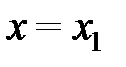 
или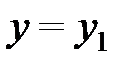 
.
3) Уравнение прямой с угловым коэффициентом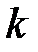 
:
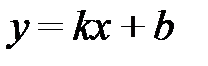; (2.6)
4) Уравнение прямой, проходящей через заданную точку 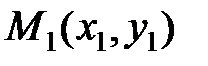и имеющей данный угловой коэффициент 
:
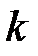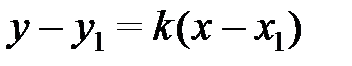. (2.7)
Если две прямые заданы уравнениями: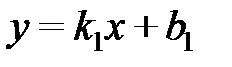 
и 
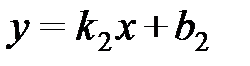, то
тангенс угла φ между двумя прямыми определяется по формуле:
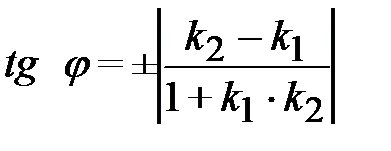, (2.8)
где знак выбирается в зависимости от того, острый или тупой угол между прямыми нужно найти.
Необходимое и достаточное условие параллельности выражается равенством:
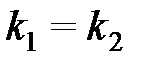. (2.9)
Необходимое и достаточное условие перпендикулярности прямых выражается равенством: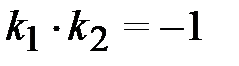 
или
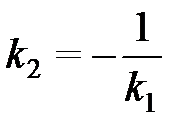. (2.10)
Расстояние d от точки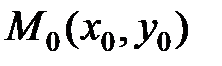 
до прямой 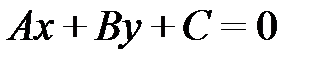можно определить по формуле:
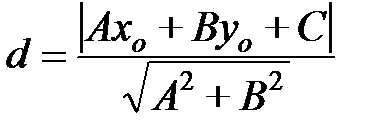. (2.11)
Для нахождения точки пересечения прямых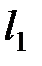 
и 
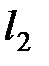необходимо решить систему уравнений, соответствующих уравнениям данных прямых.
Задача 1. Даны вершины А (–2; 3), В (1; 12), С (11; 6) треугольника АВС. Необходимо: 1) сделать чертеж. Найти:
2) уравнение стороны АВ; 3) длину стороны АВ; 4) уравнение высоты, опущенной из вершины С; 5) длину этой высоты; 6) уравнение прямой, параллельной стороне АВ, проходящей через вершину С; 7) площадь треугольника; 8) уравнение медианы, опущенной из вершины С; 9) точку пересечения высот 10) внутренний угол треугольника АВС.
Решение:
1) Выполним чертеж в прямоугольной декартовой системе координат:
 | |
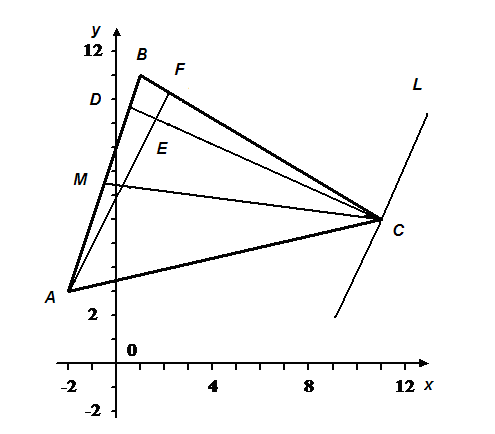| Рисунок 2.1 |
2) Для нахождения уравнения стороны АВ воспользуемся уравнением прямой, проходящим через две точки. Подставим в (2.5) координаты точек А и В:
; 
;
; 
;
; 
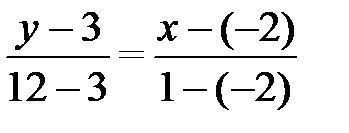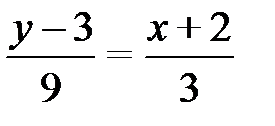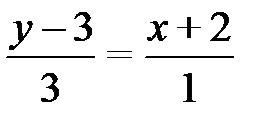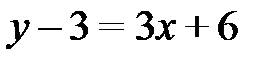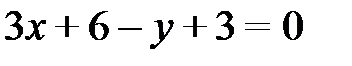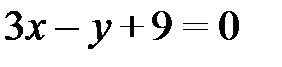– получено общее уравнение прямой АВ.
3) Длину стороны АВ найдем по формуле расстояния между двумя точками. Подставим в(2.1) координаты точек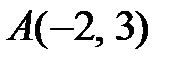 
и 
= 
= 
= 
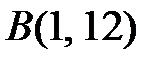
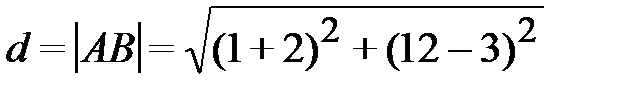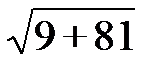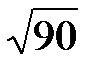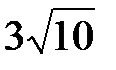ед.
4) Высота CD, проведенная к стороне AB перпендикулярна ей,и поэтому, чтобы воспользоваться условием перпендикулярности (2.10) запишем уравнение прямой АВ: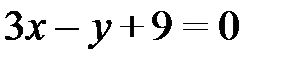 
в виде уравнения прямой с угловым коэффициентом (2.6): 
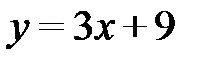. Следовательно, 
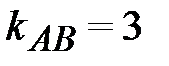. Угловые коэффициенты 
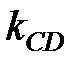и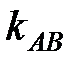 
удовлетворяют условию (2.10), т.е.: 
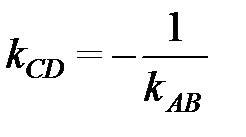и угловой коэффициент высоты CD будет равен 
.
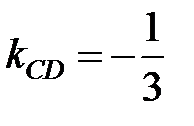Напишем уравнение высоты CD, используя уравнение прямой, проходящей через заданную точку и имеющей данный угловой коэффициент:
Подставляя в (2.7)координаты точки С(11; 6) и угловой коэффициент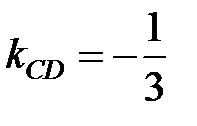 
получим: 
, 
, 
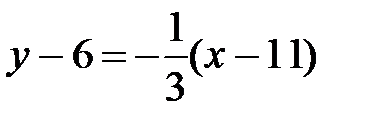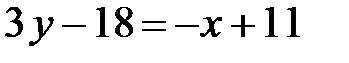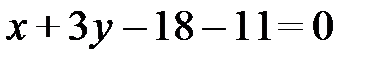или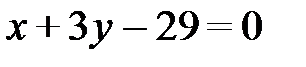 
– общее уравнение прямой CD.
5) Длину высоты СD, найдем как расстояние от точки С(11; 6) до прямой АВ: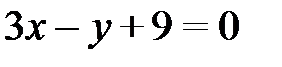 
, используя формулу (2.11):
.
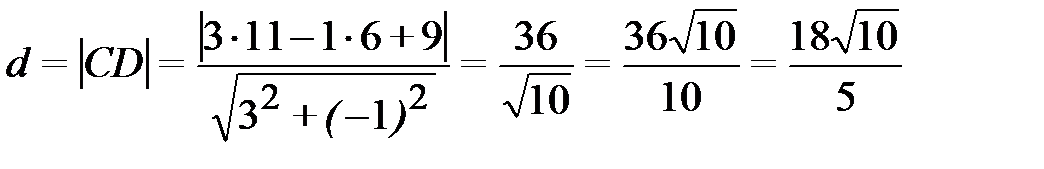6) Уравнение прямой СL, параллельной стороне АВ, проходящей через вершину С напишем, используя условие параллельности (2.9), т.е.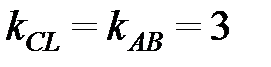 
. В уравнение (2.7) подставим координаты точки С (11; 6) и значение углового коэффициента 
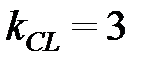, получим: 
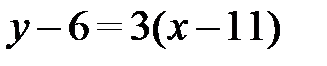, или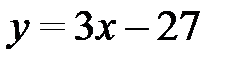 
.
Итак,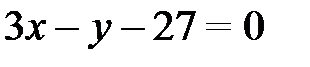 
- общее уравнение прямой СL.
7) Площадь треугольника найдем по формуле:
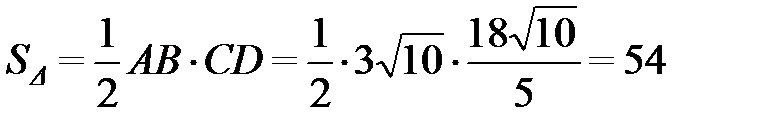ед2.
8) Для нахождения уравнения медианы CM, найдем координаты точки М. Точка М делит сторону АВ пополам, тогда по формулам деления отрезка пополам (2.3) координаты точки М будут равны :
, 
.
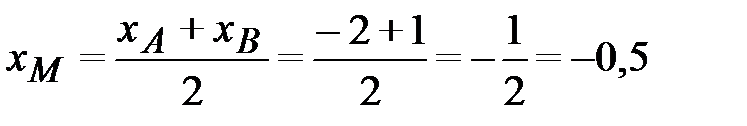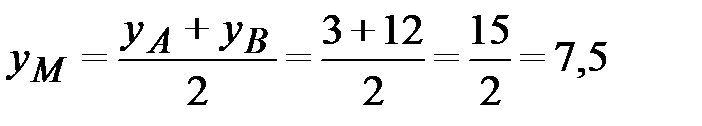Уравнение медианы СМ получим, подставив координаты точек C(11; 6)и
М(-0,5; 7,5) в формулу (2.5):
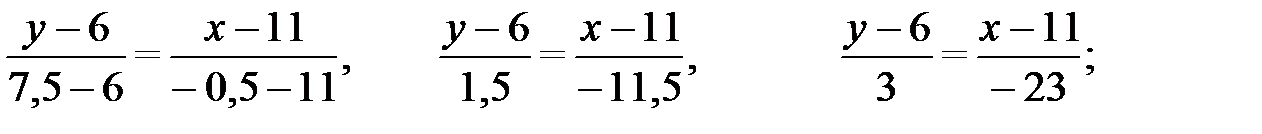
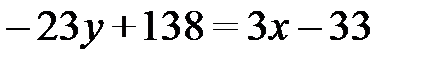или 
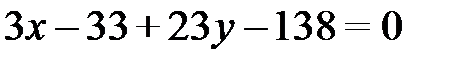
Итак: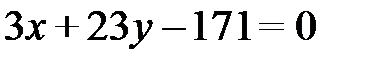 
– общее уравнение медианы СМ.
9) Для нахождения точки пересечения высот треугольника АВС необходимо найти уравнение еще одной высоты, например проведенной из вершины A, т.к. все три высоты пересекаются в одной точке. Найдем уравнение высоты AF аналогично тому, как находили уравнение высоты CD в пункте 3). Для этого напишем уравнение стороны ВС по формуле (2.5), используя координаты точек В(1; 12) и С(11; 6), тогда
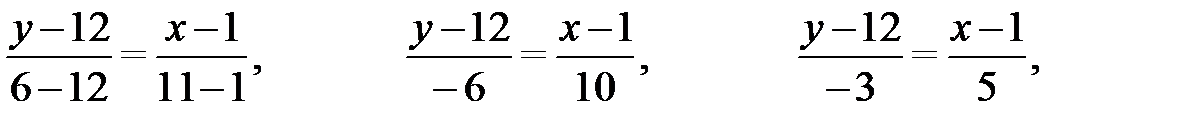
или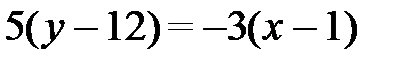 
, 
.
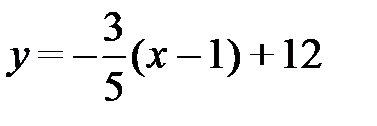Следовательно, для прямой ВС угловой коэффициент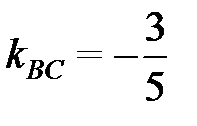 
.
Угловой коэффициент прямой AF из условия (2.10) будет:
.
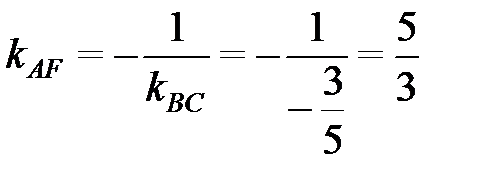Подставляя в (2.7) координаты точки А(-2; 3) и угловой коэффициент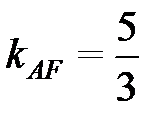 
, получим уравнение высоты AF: 
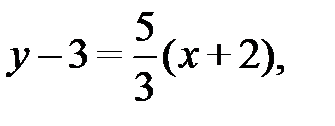или
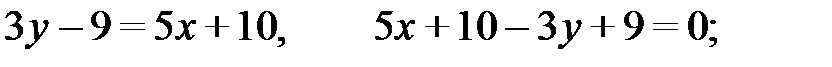
Итак,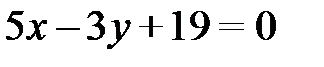 
– общее уравнение высоты AF.
Решая систему уравнений, соответствующих прямым CD и AF, найдем точку пересечения высот:
, 
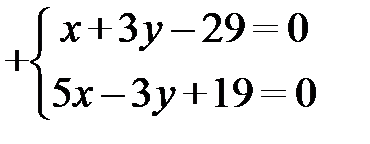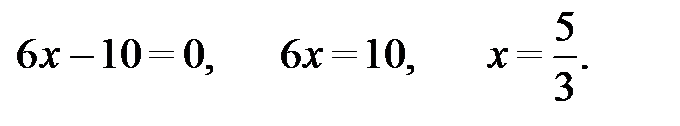
Подставим в первое уравнение системы и получим:
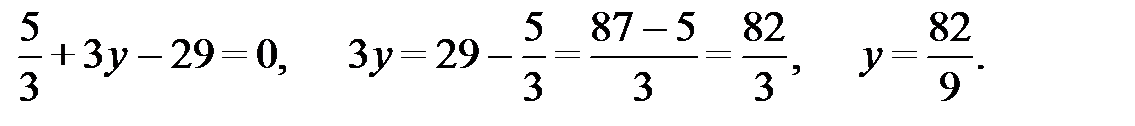
Итак, точка Е пересечения высот имеет координаты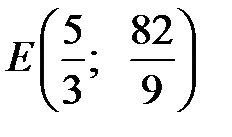 
.
10) Для нахождения угла АВС используем формулу (2.8), где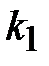 
– угловой коэффициент прямой АВ и 
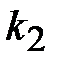- угловой коэффициент прямой ВС, т.е. 
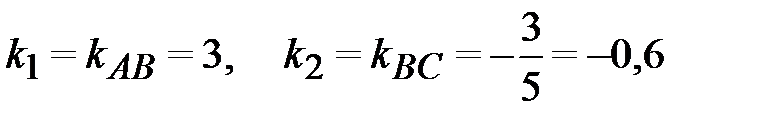, причем по рисунку видно, что этот угол 
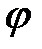меньше 
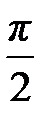, следовательно, 
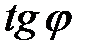должен быть положительным.
Итак,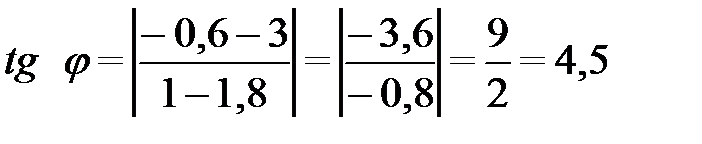 
или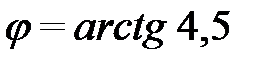 
.
Задания и варианты для индивидуального решения
Задание 1.Даны определител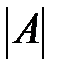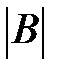и 
, 
и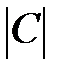 
.
а) Вычислить 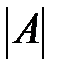и 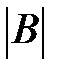по определению;
б) Вычислить 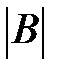и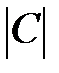 
разложением по первой строке;
в) Вычислить 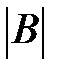и 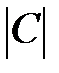разложением по второму столбцу;
г) Для определителей 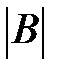и , и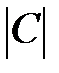спользуя свойства, обнулить все элементы какого-либо ряда, кроме одного. Вычислить их, разлагая по элементам полученного ряда;
д) Определител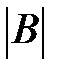и и 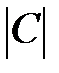, используя свойства, привести к треугольному виду и вычислить их значения.
Вариант 1.
, 
, 
.
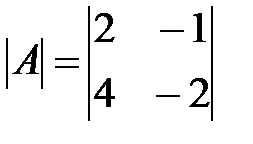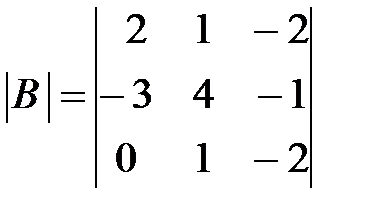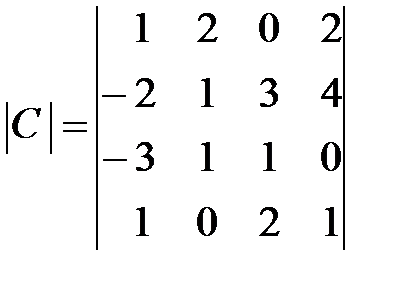Вариант 2.
, 
, 
.
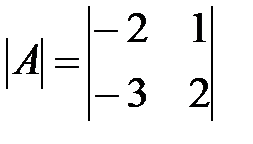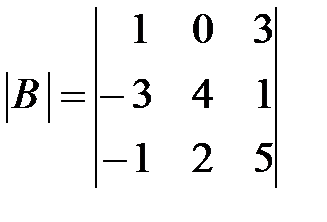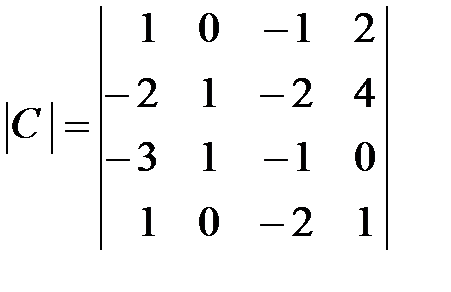Вариант 3.
, 
, 
.
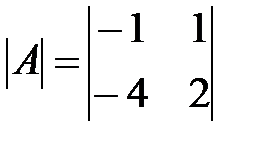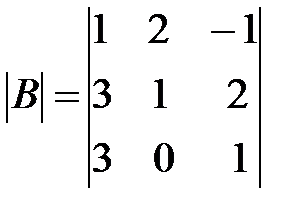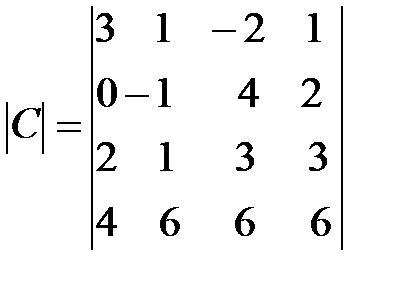Вариант 4.
, 
, 
.
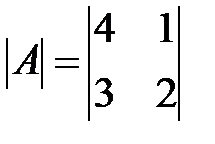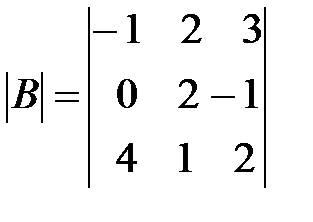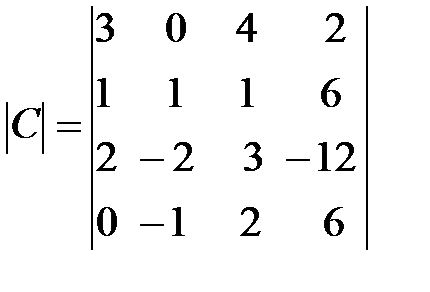Вариант 5.
, 
, 
.
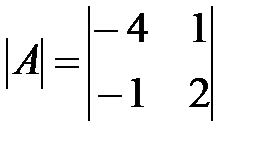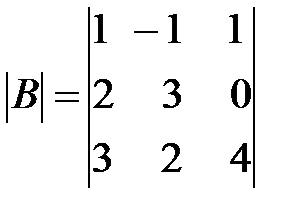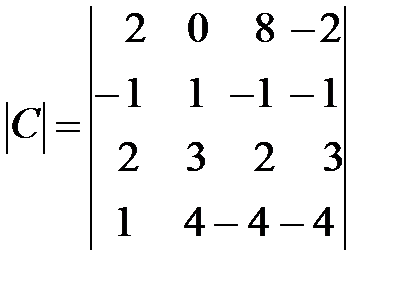Вариант 6.
, 
, 
.
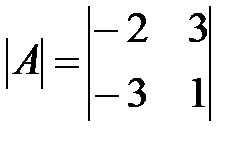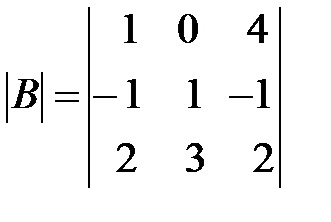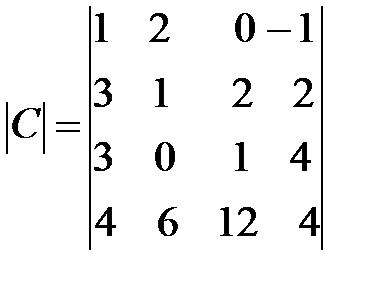Вариант 7.
, 
, 
.
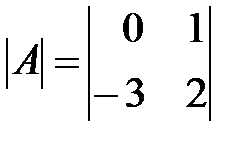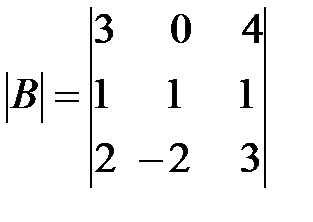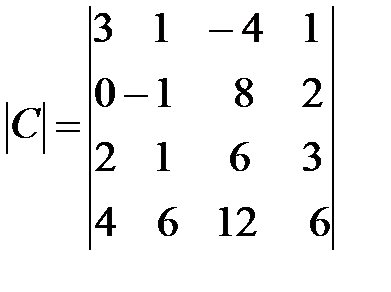Вариант 8.
, 
, 
.
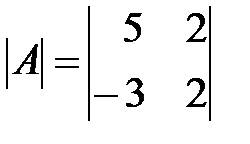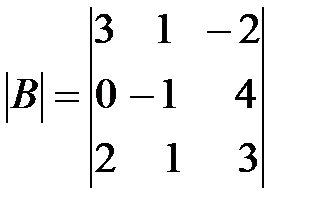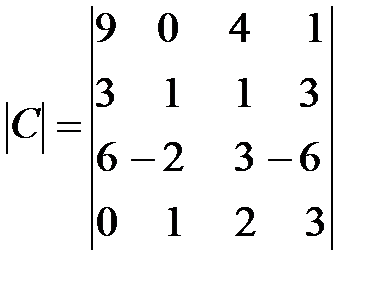Вариант 9.
, 
, 
.
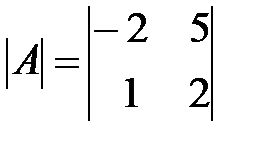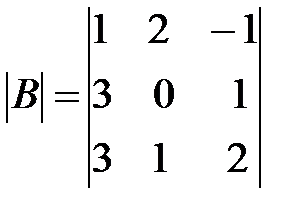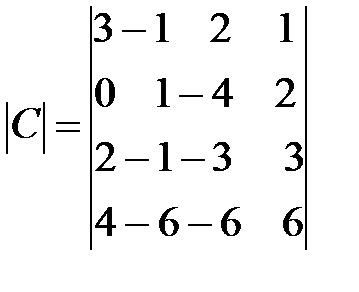Вариант 10.
, 
, 
.
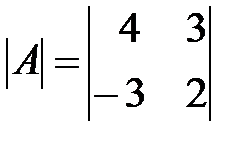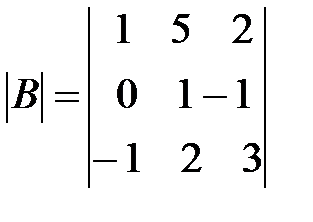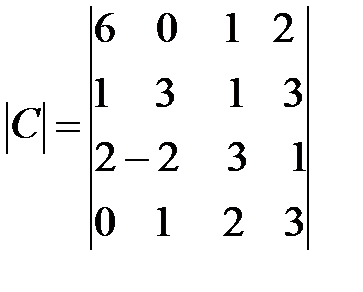Вариант 11.
, 
, 
.
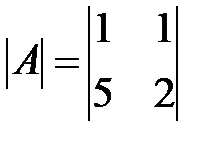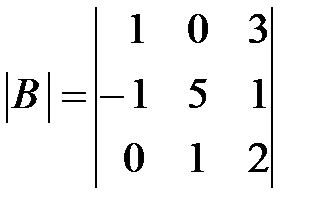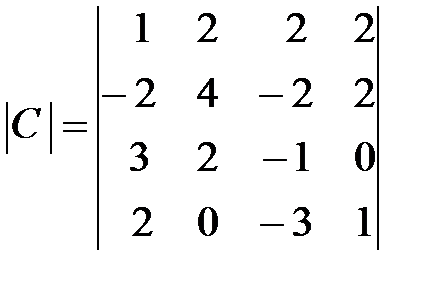Вариант 12.
, 
, 
.
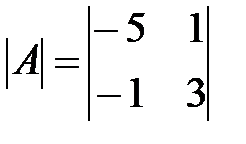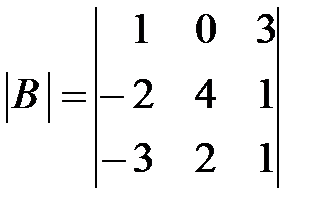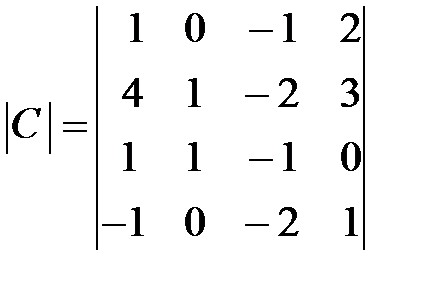Вариант 13.
, 
, 
.
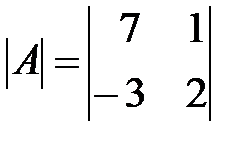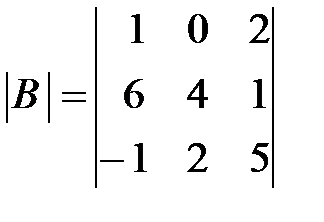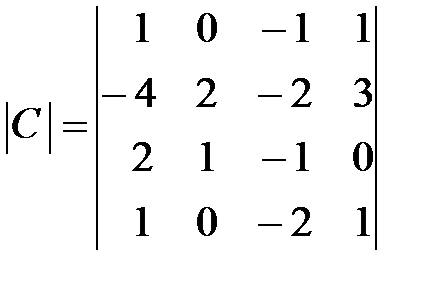Вариант 14.
, 
, 
.
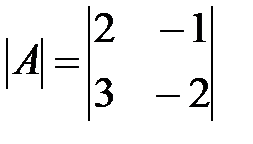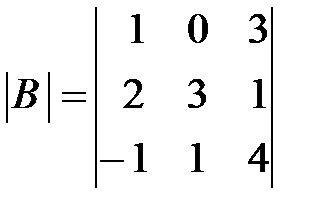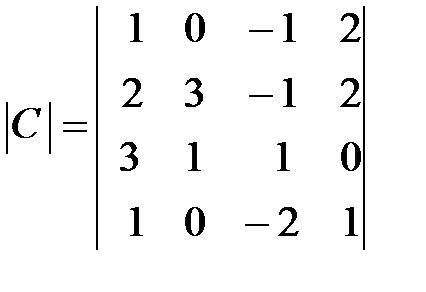Вариант 15.
, 
, 
.
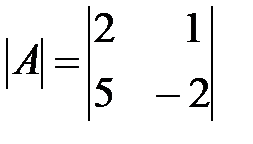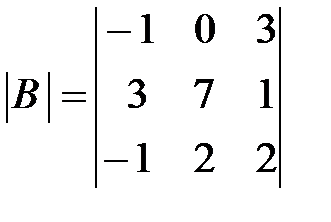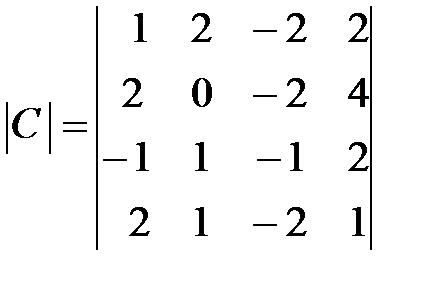Вариант 16.
, 
, 
.
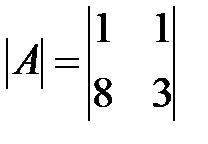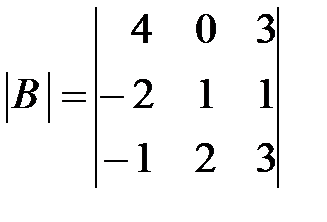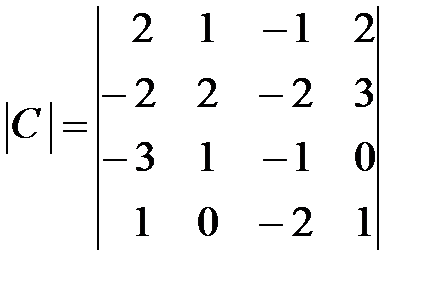Вариант 17.
, 
, 
.
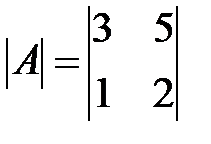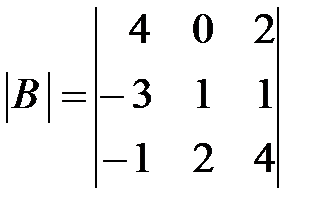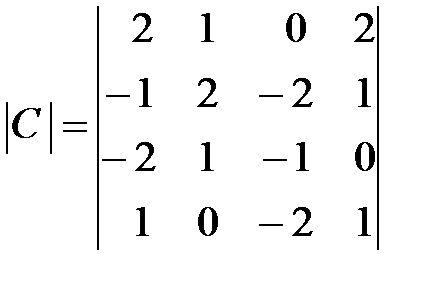Вариант 18.
, 
, 
.
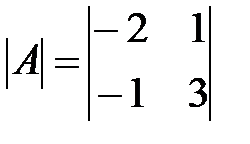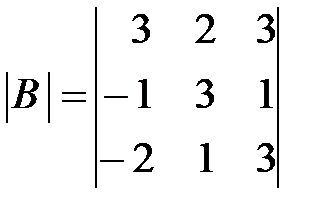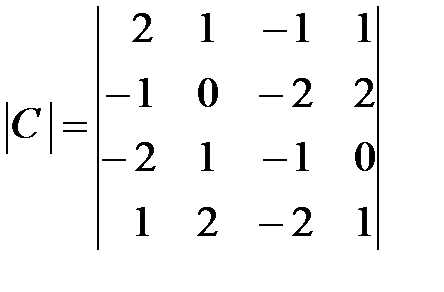Вариант 19.
, 
, 
.
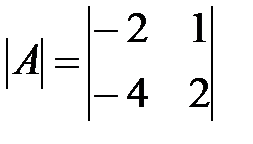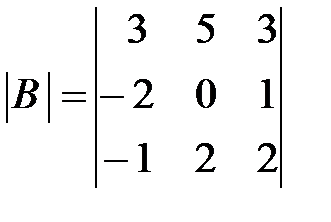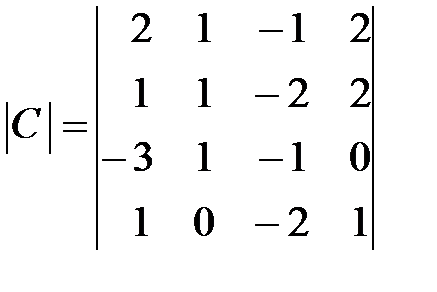Вариант 20.
, 
, 
.
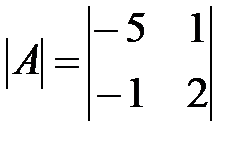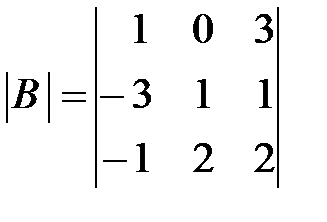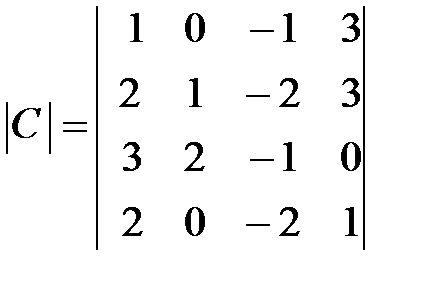Вариант 21.
, 
, 
.
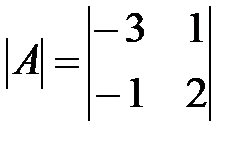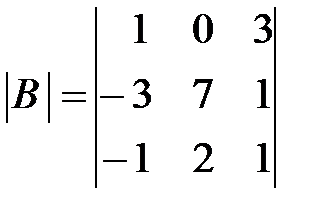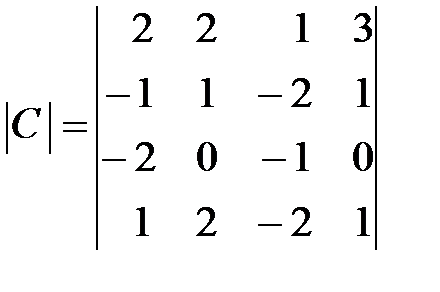Вариант 22.
, 
, 
.
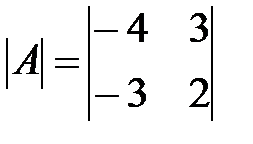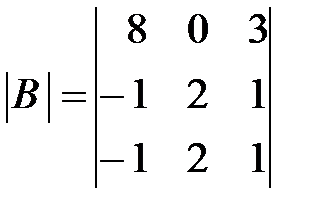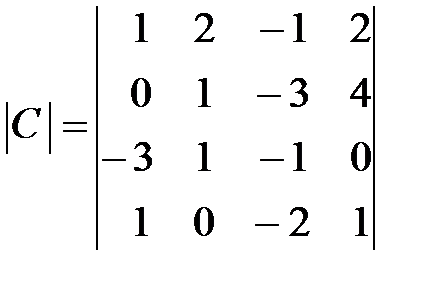Вариант 23.
, 
, 
.
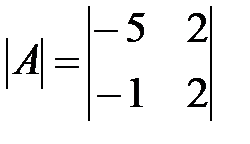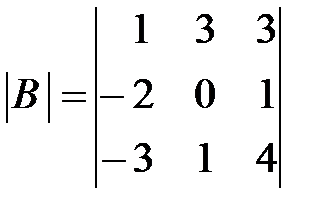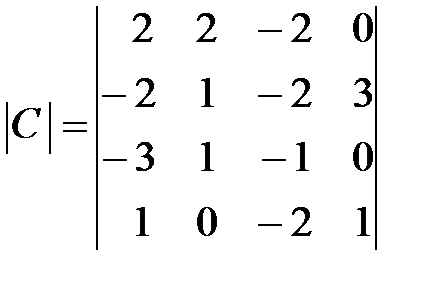Вариант 24.
, 
, 
.
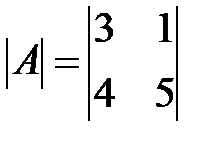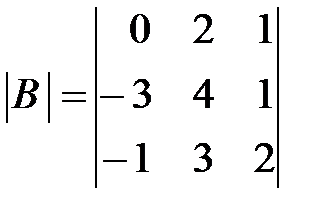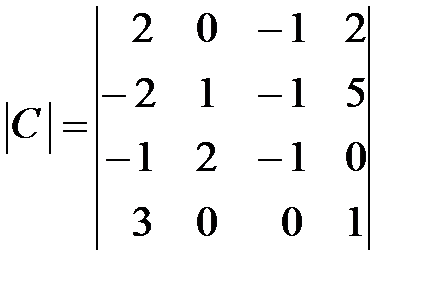Вариант 25.
, 
, 
.
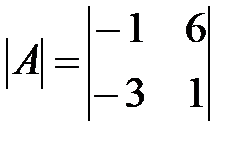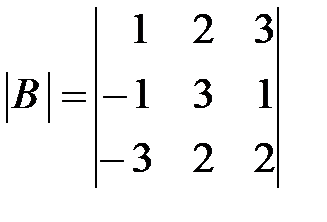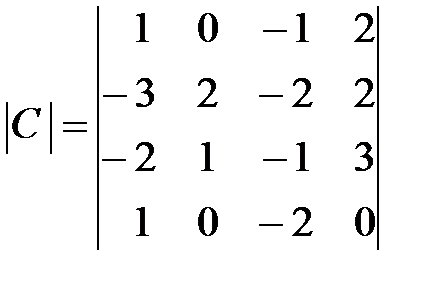Вариант 26.
, 
, 
.
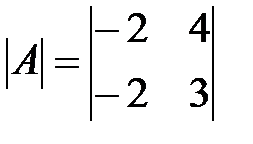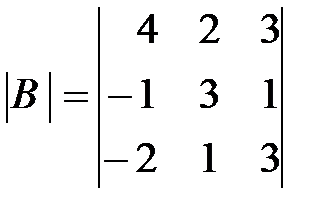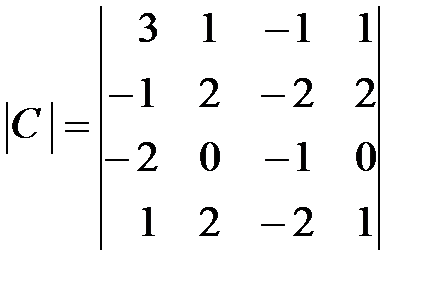Вариант 27.
, 
, 
.
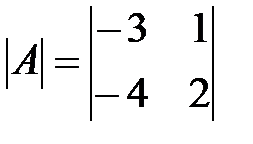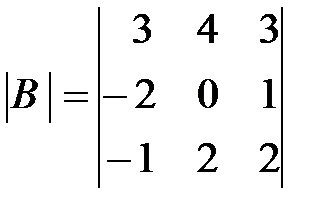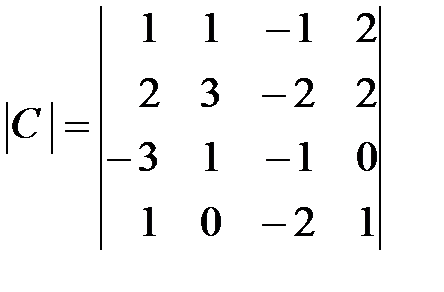Вариант 28.
, 
, 
.
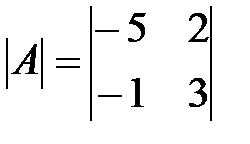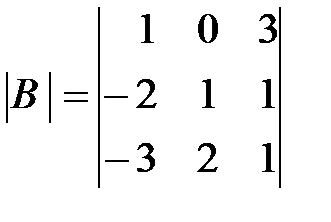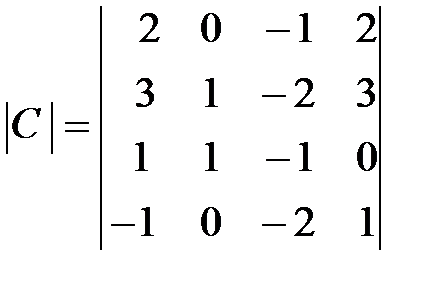Вариант 29.
, 
, 
.
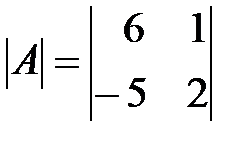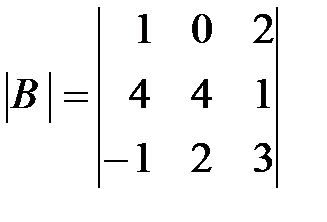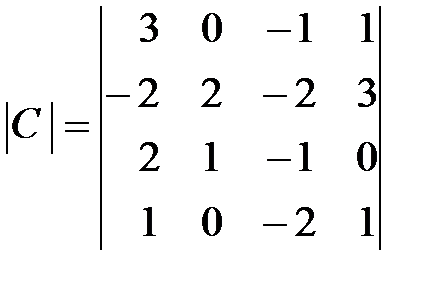Вариант 30.
, 
, 
.
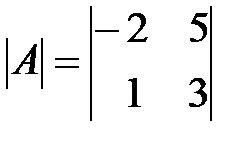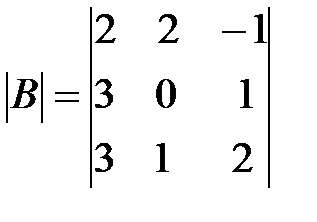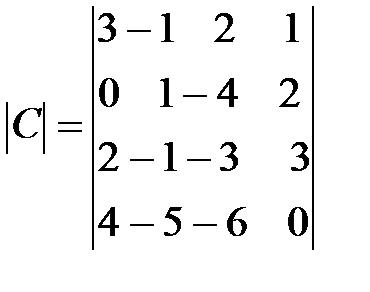Задание 2. Даны матрицы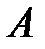 
, 
, 
, 
, 
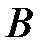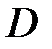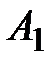и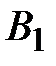 
.
1.Найти:
а)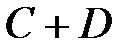 
, 
, 
, 
;
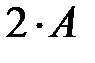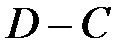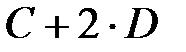б)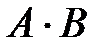 
, 
, 
, 
, 
;
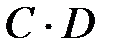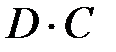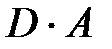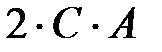в)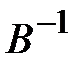 
, 
, 
, 
.
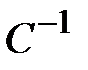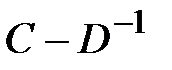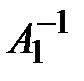2.Найти ранги матриц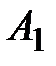 
и 
.
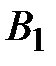Вариант 1.
, 
, 
, 
,
, 
.
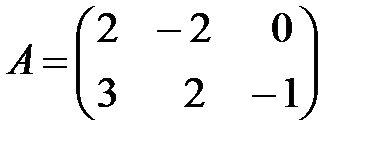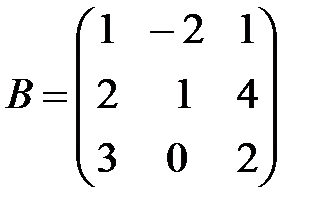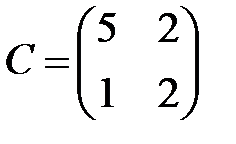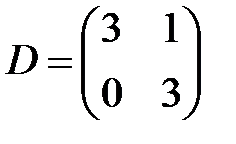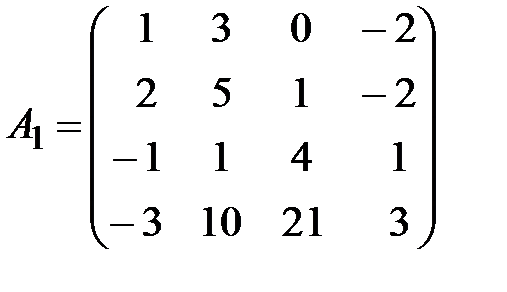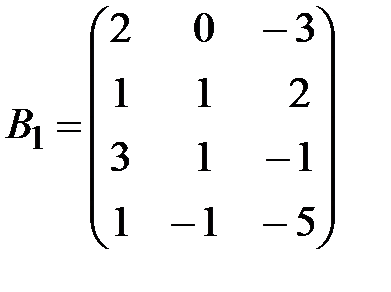Вариант 2.
, 
, 
, 
,
, 
.
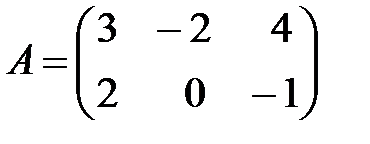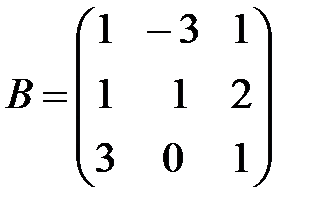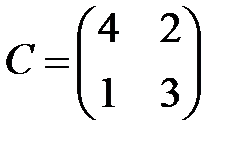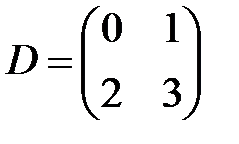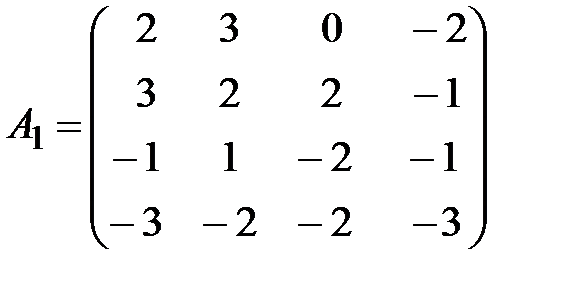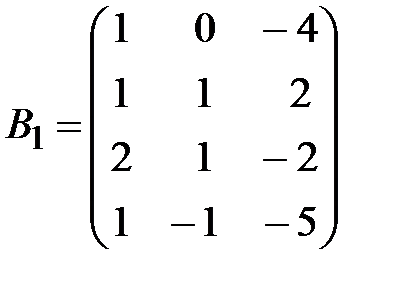Вариант 3.
, 
, 
, 
,
, 
.
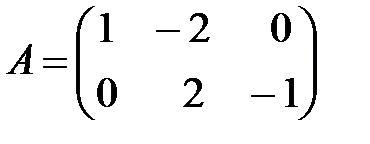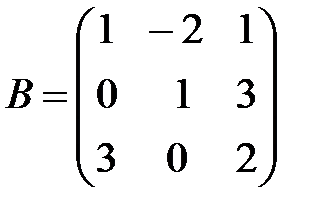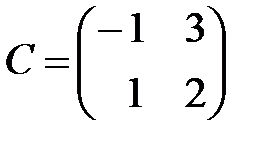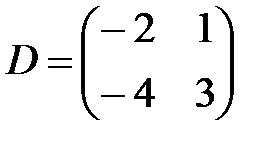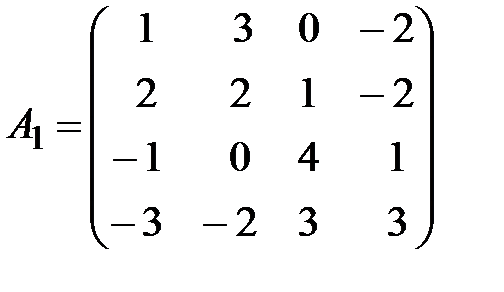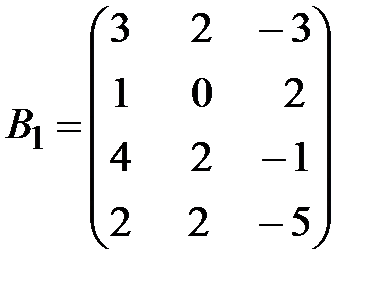Вариант 4.
, 
, 
, 
,
, 
.
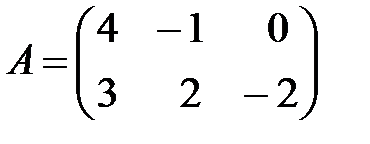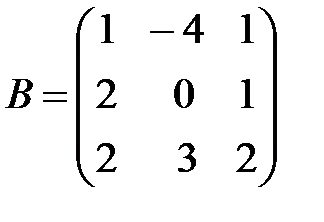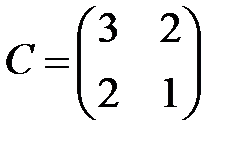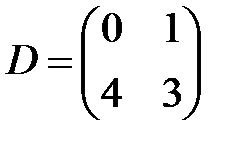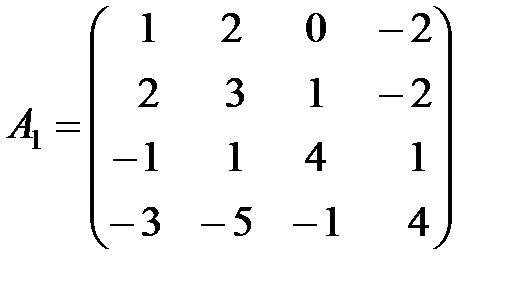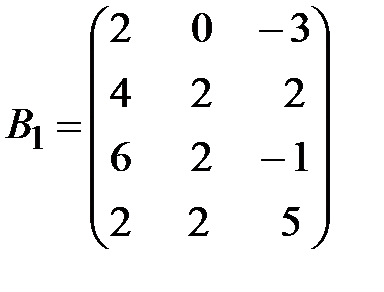Вариант 5.
, 
, 
, 
,
, 
.
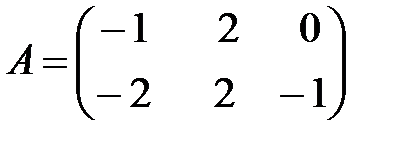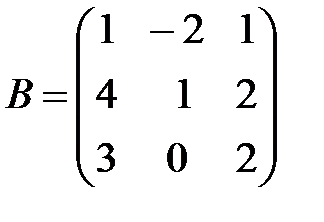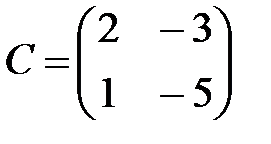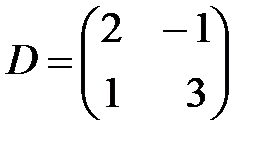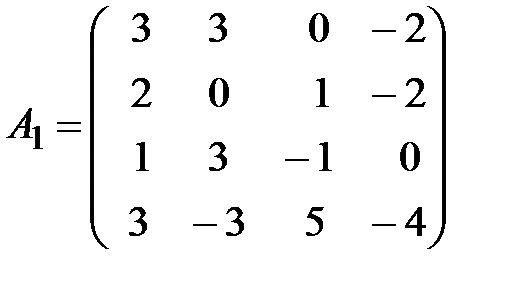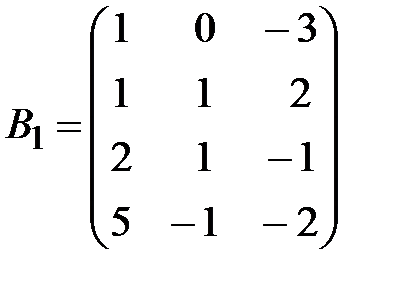Вариант 6.
, 
, 
, 
,
, 
.
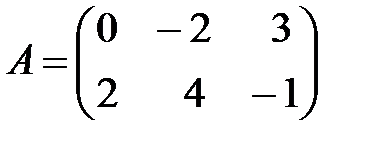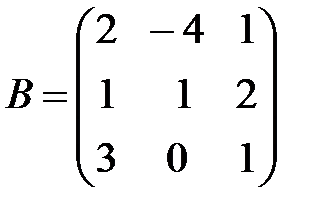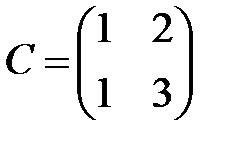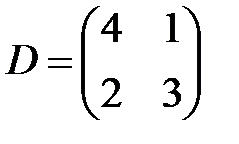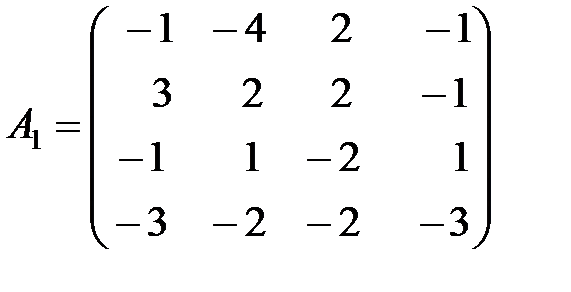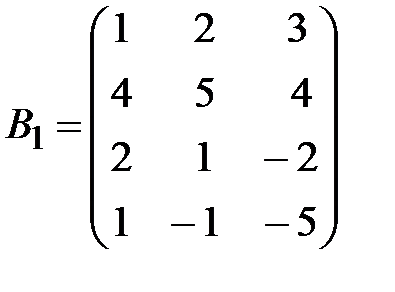Вариант 7.
, 
, 
, 
,
, 
.
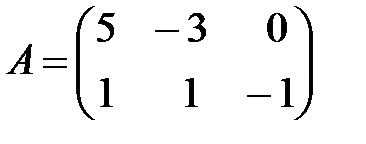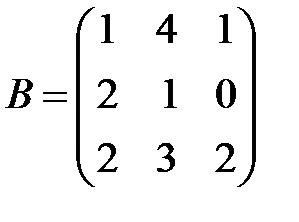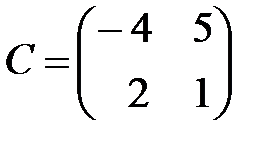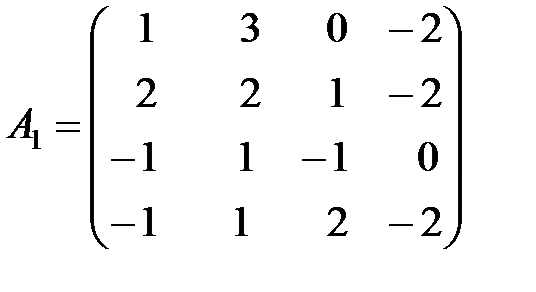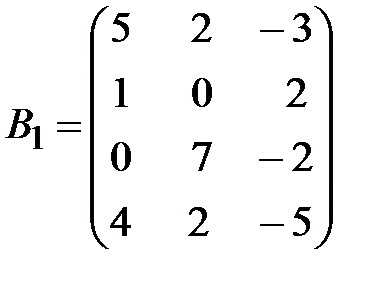Вариант 8.
, 
, 
, 
,
, 
.
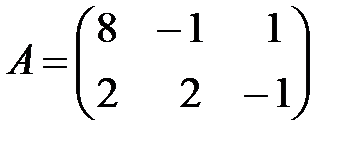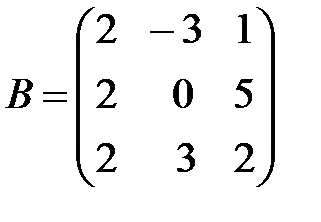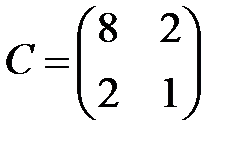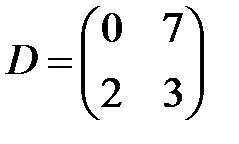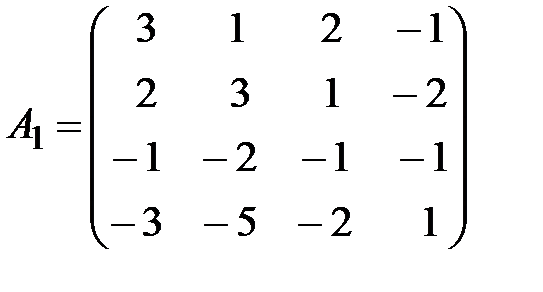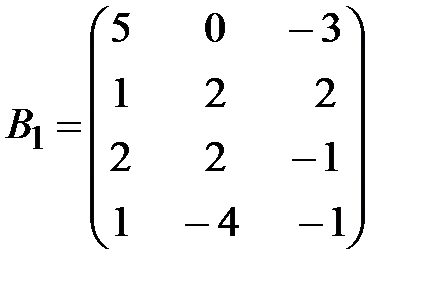Вариант 9.
, 
, 
, 
,
, 
.
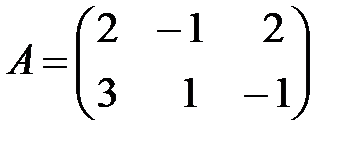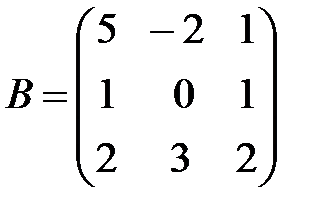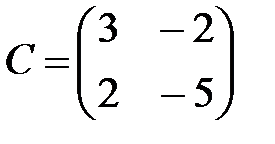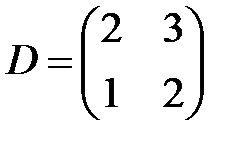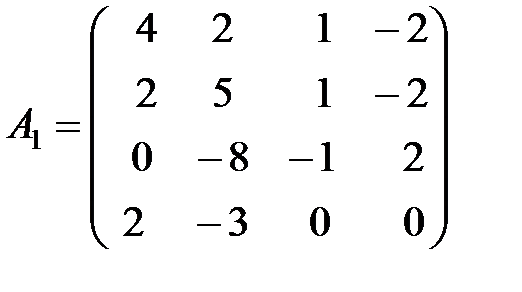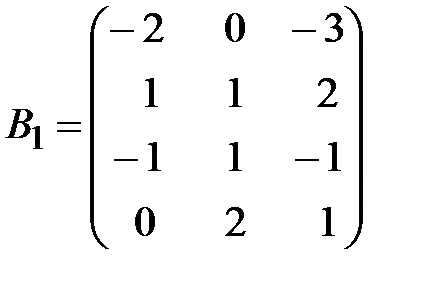Вариант 10.
, 
, 
, 
,
, 
.
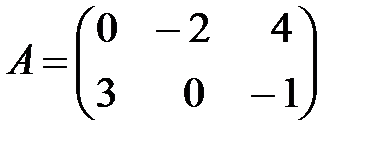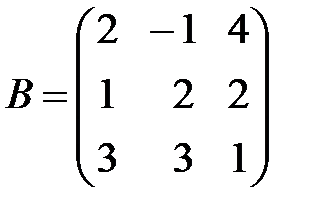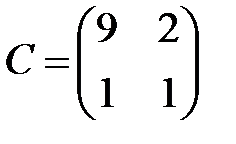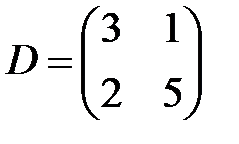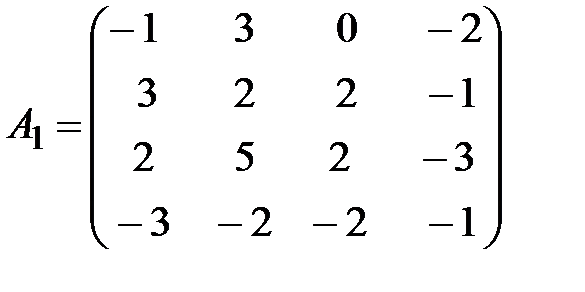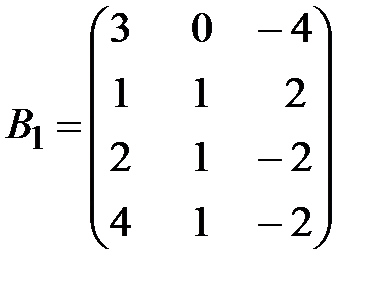Вариант 11.
, 
, 
, 
,
, 
.
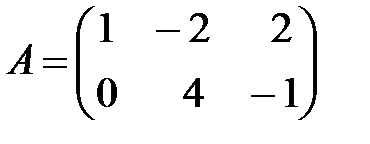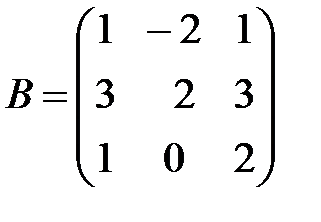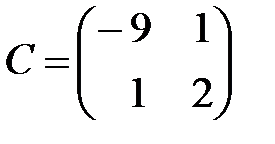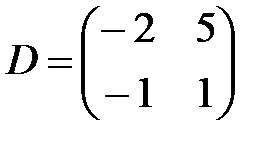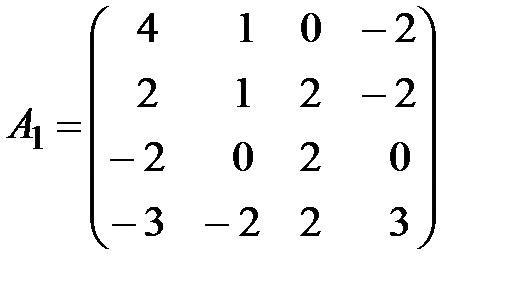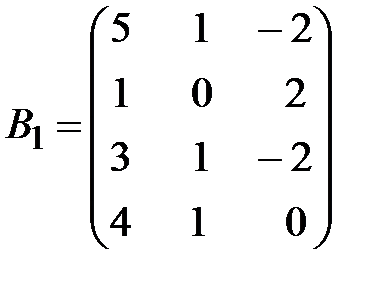Вариант 12.
, 
, 
, 
,
, 
.
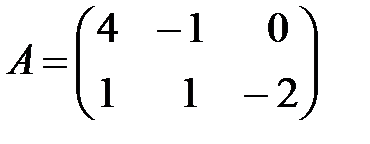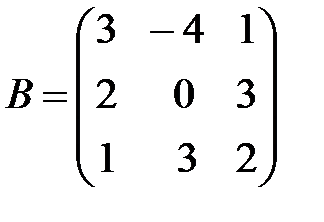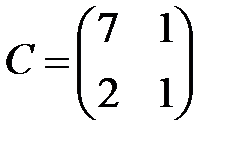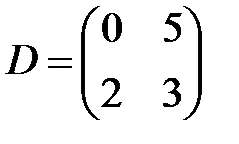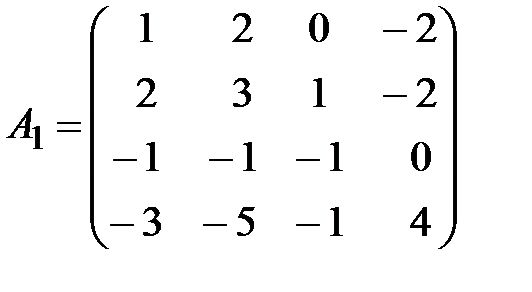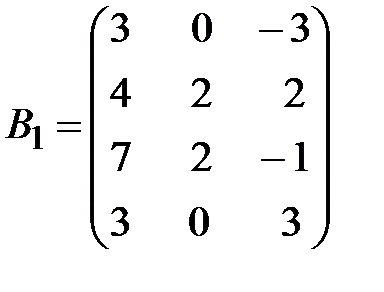Вариант 13.
, 
, 
, 
,
, 
.
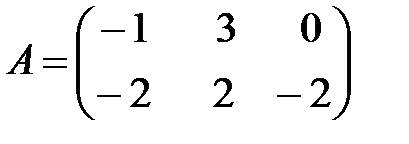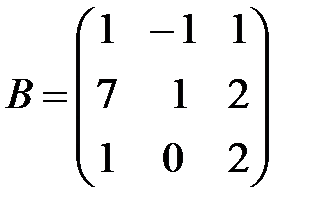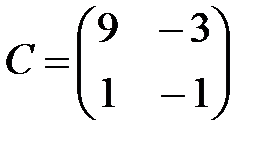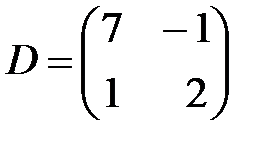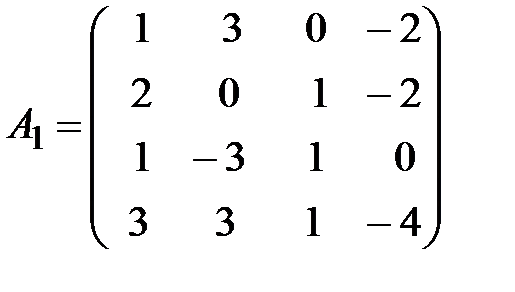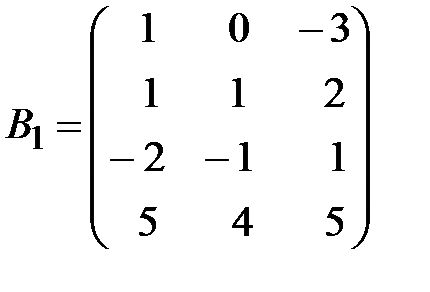Вариант 14.
, 
, 
, 
,
, 
.
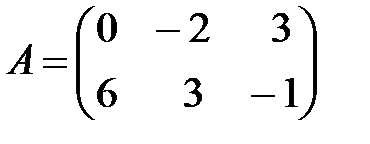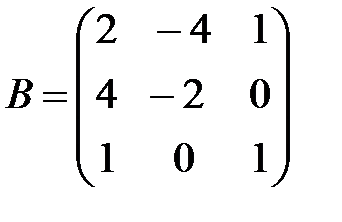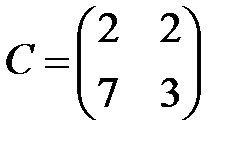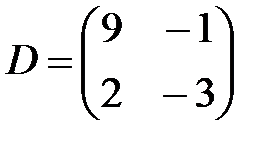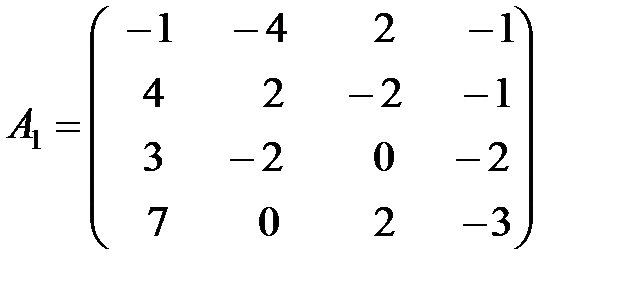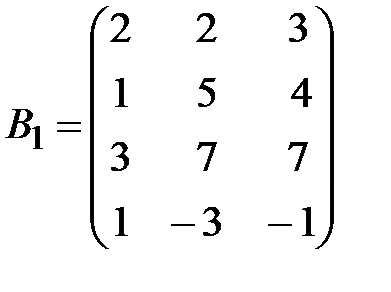Вариант 15.
, 
, 
, 
,
, 
.
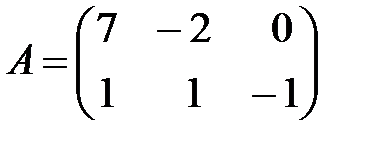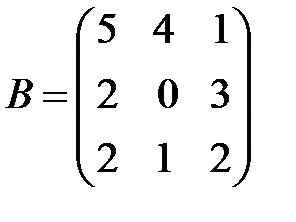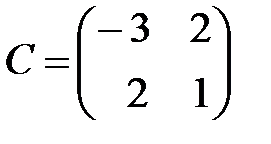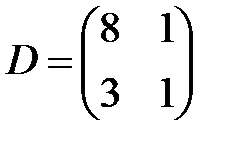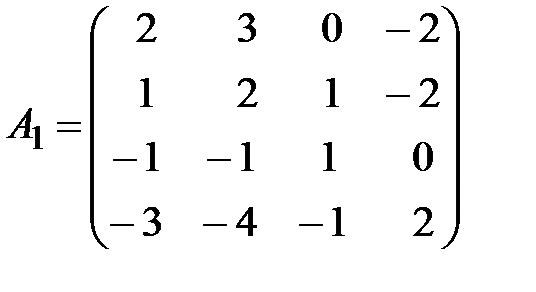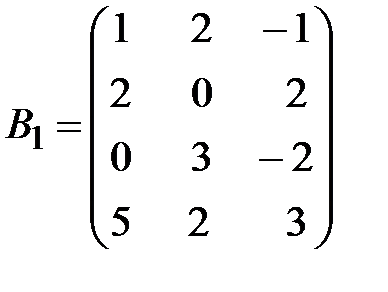Вариант 16.
, 
, 
, 
,
, 
.
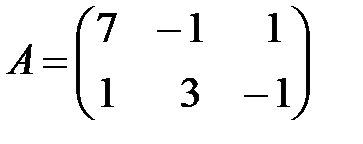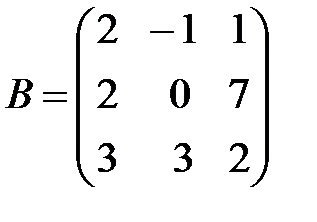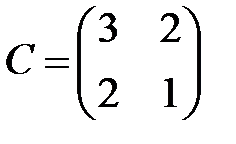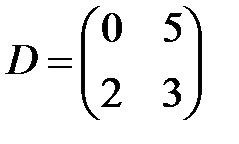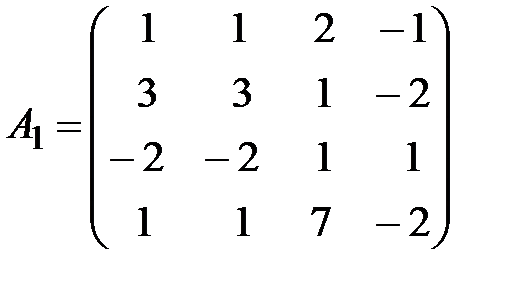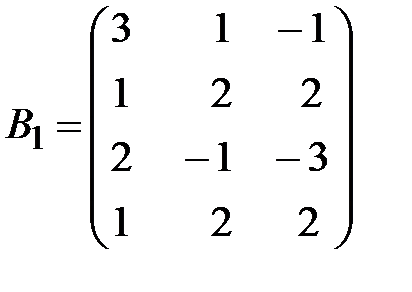Вариант 17.
, 
, 
, 
,
, 
.
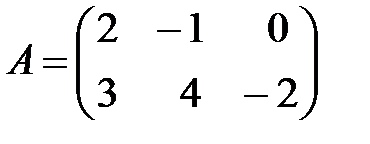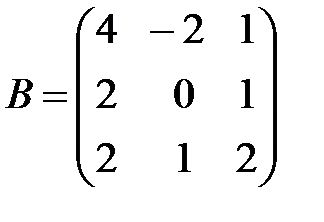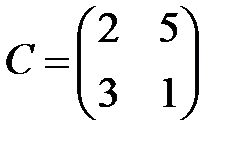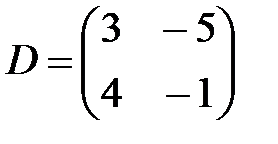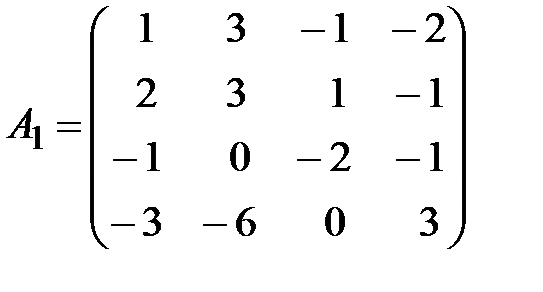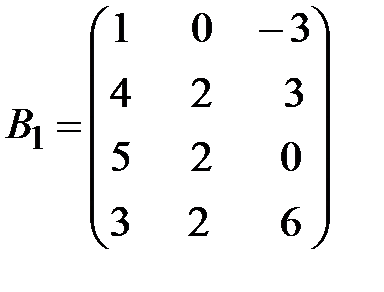Вариант 18.
, 
, 
, 
,
, 
.
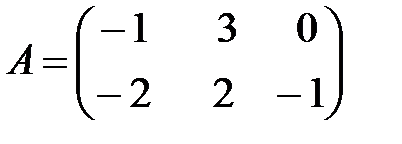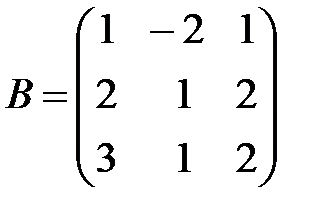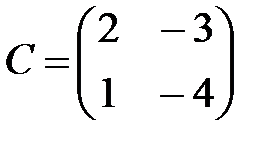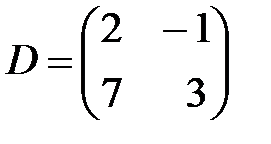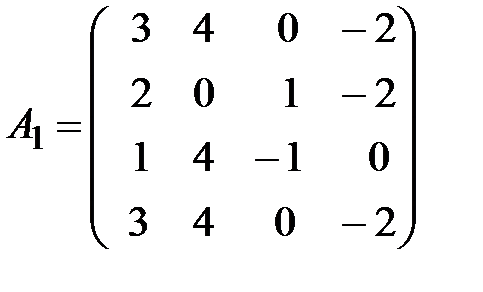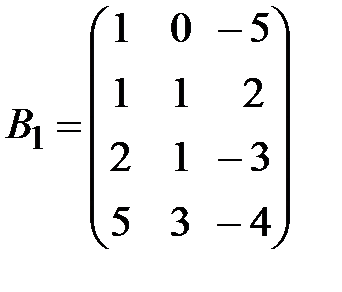Вариант 19.
, 
, 
, 
,
, 
.
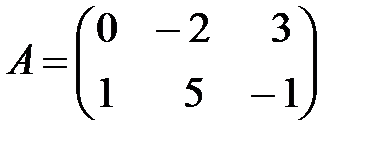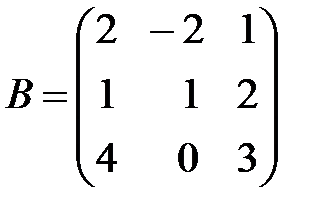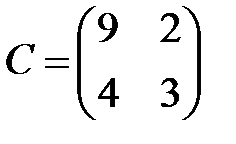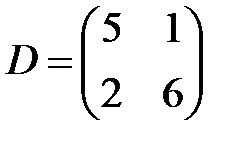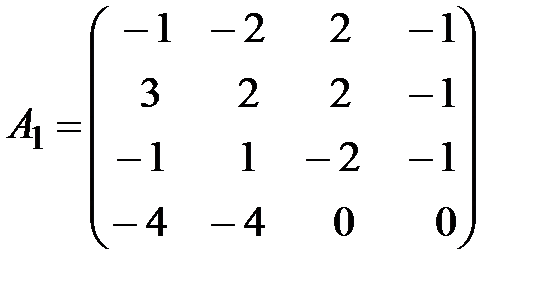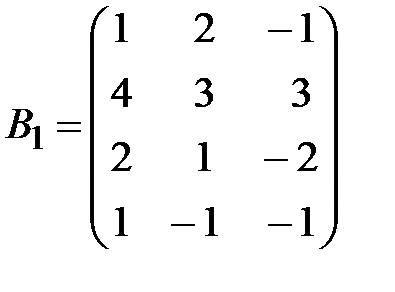Вариант 20.
, 
, 
, 
,
, 
.
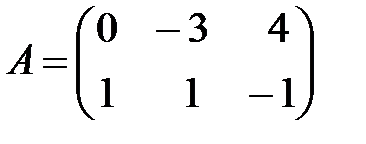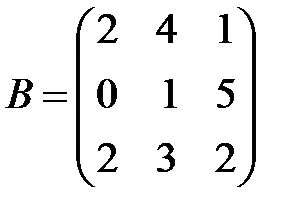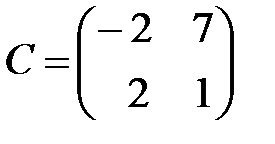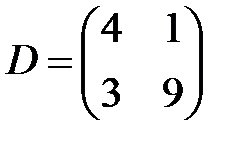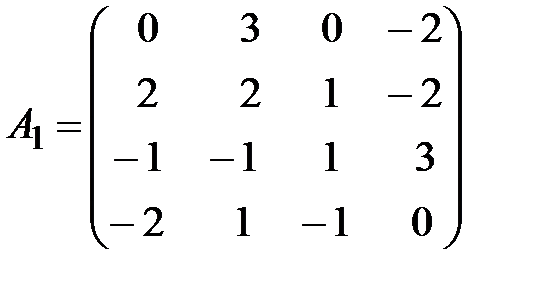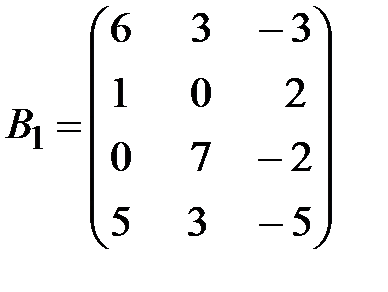Вариант 21.
, 
, 
, 
,
, 
.
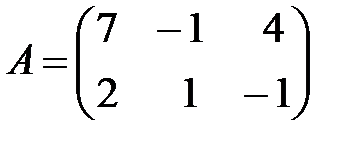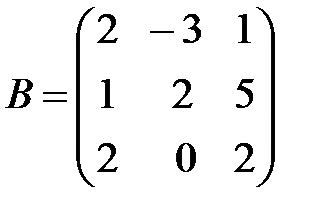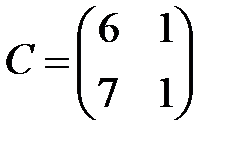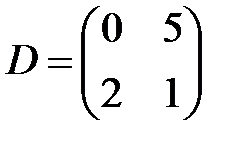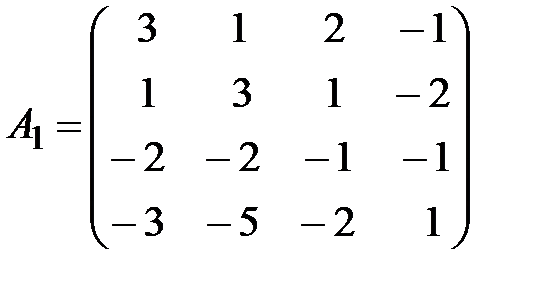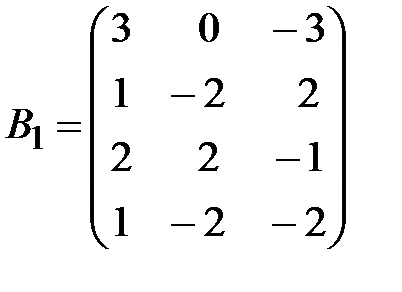Вариант 22.
, 
, 
, 
,
, 
.
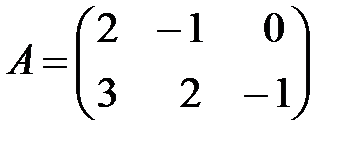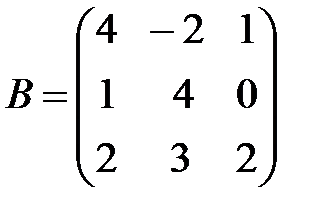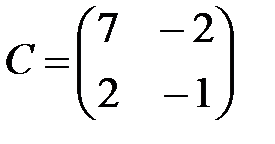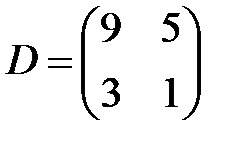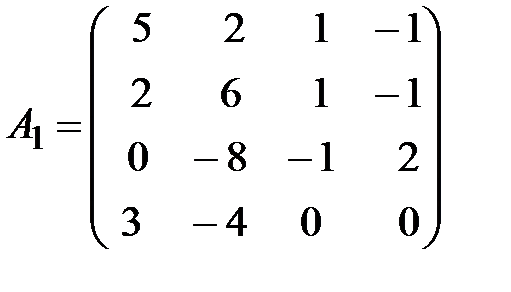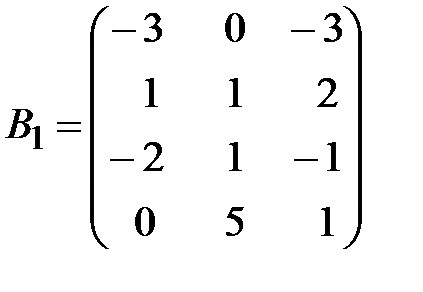Вариант 23.
, 
, 
, 
,
, 
.
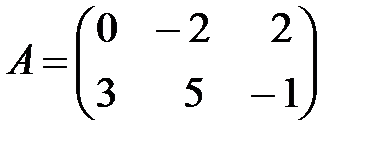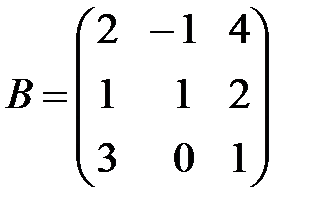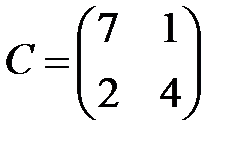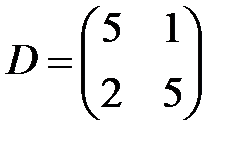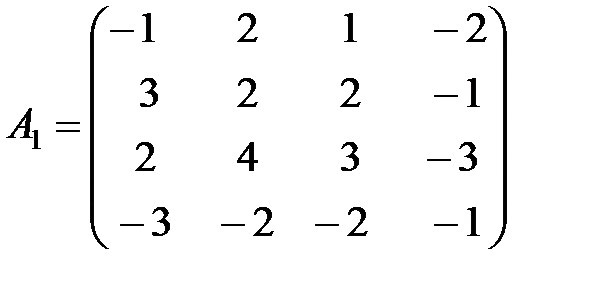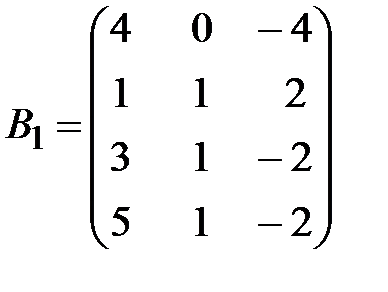Вариант 24.
, 
, 
, 
,
, 
.
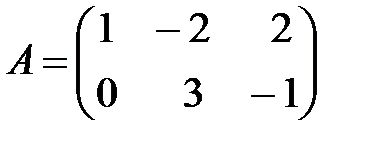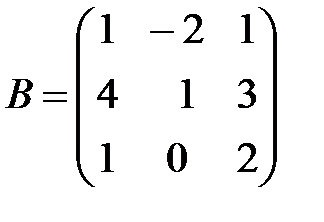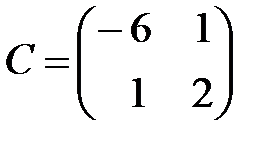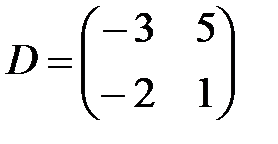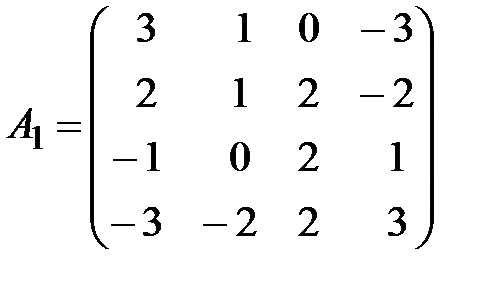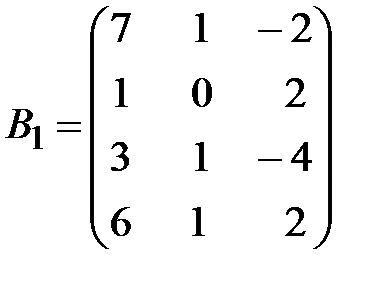Вариант 25.
, 
, 
, 
,
, 
.
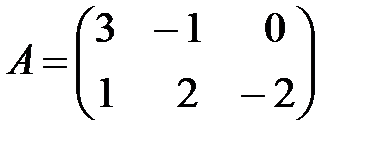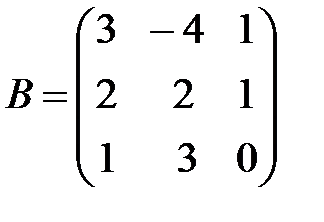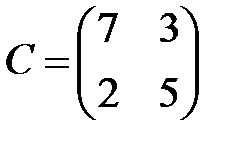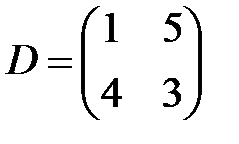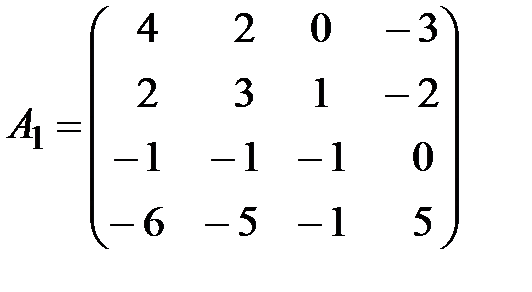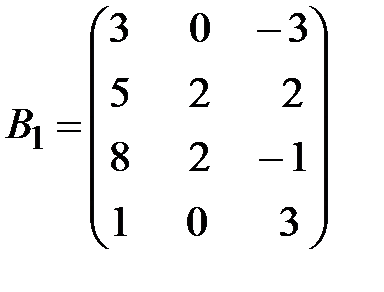Вариант 26.
, , , ,
, .
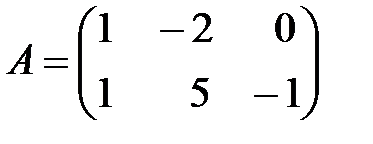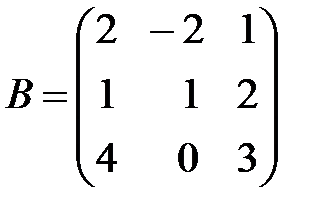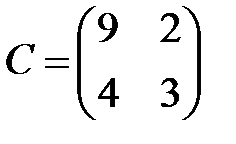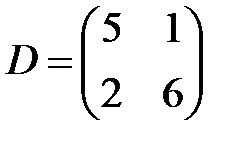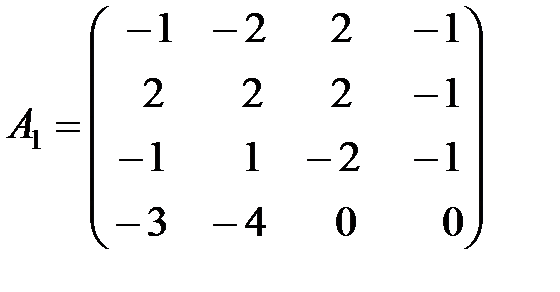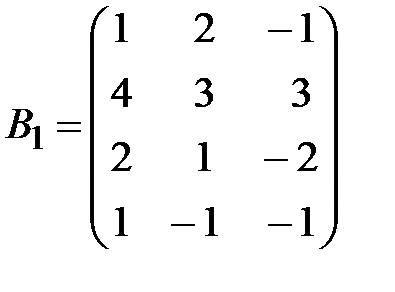Вариант 27.
, , , ,
, .
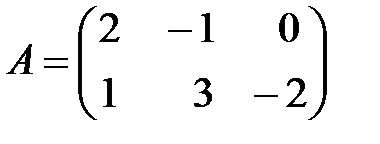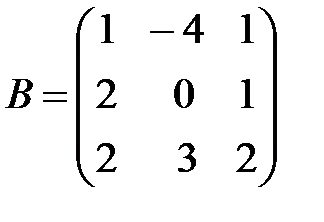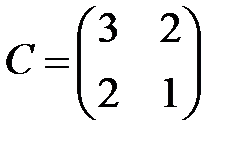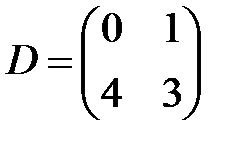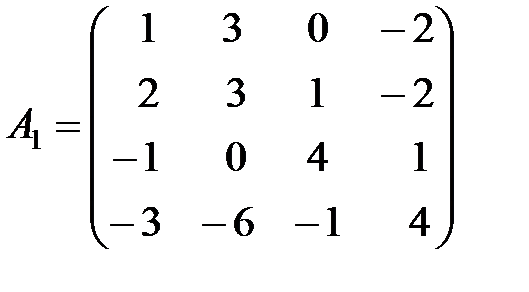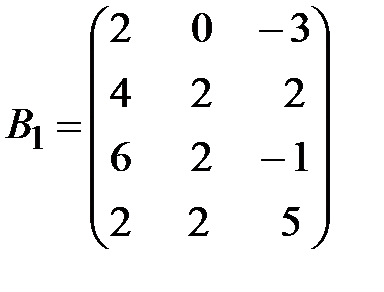Вариант 28.
, , , ,
, .
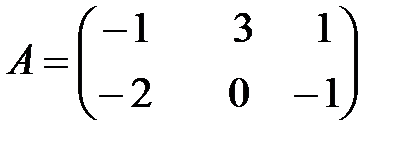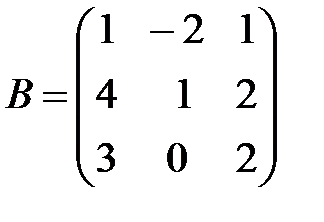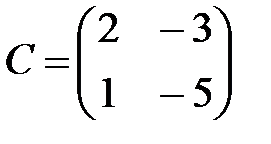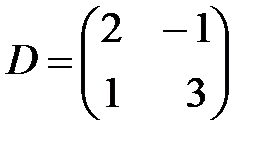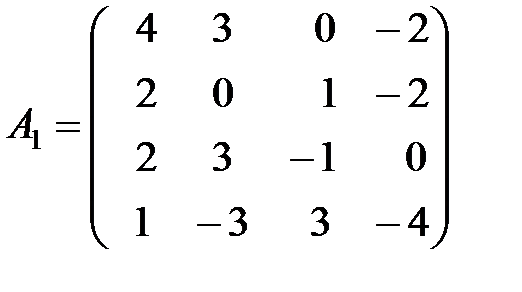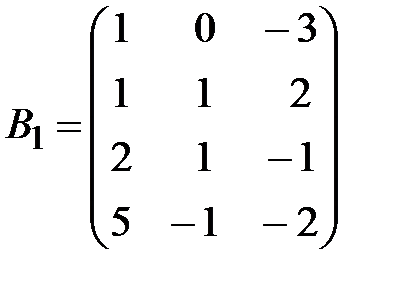Вариант 29.
, , , ,
, .
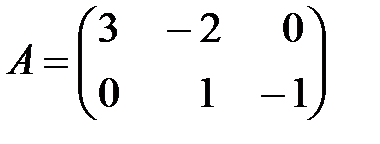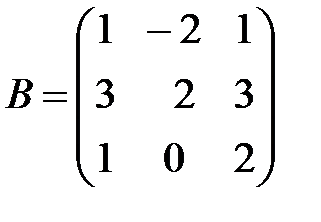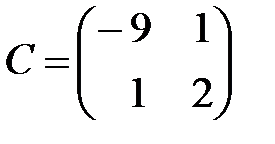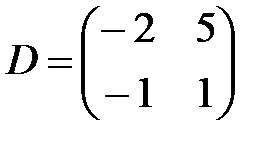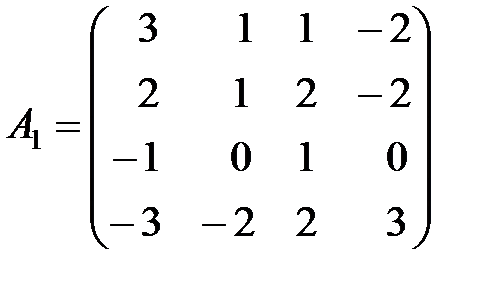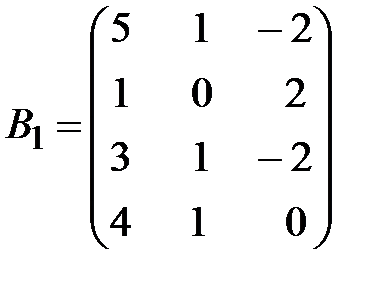Вариант 30.
, 
, 
, ,
, .
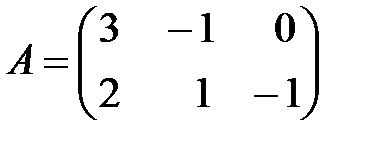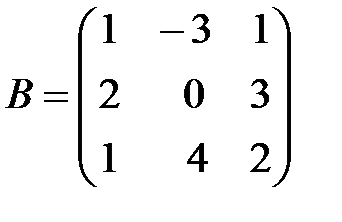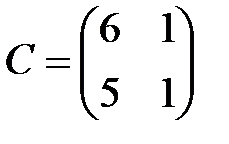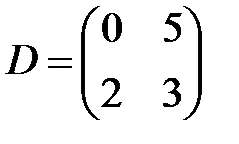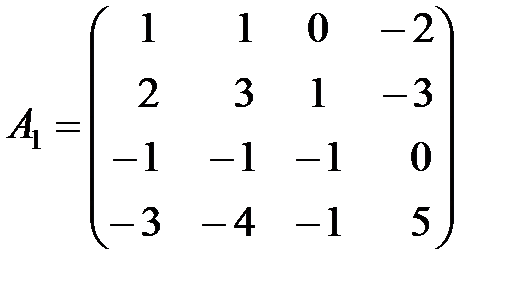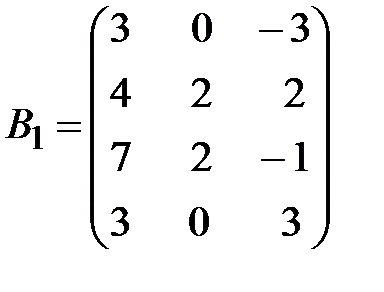Задание 3.В трех магазинах продаются два вида растительного масла. Матрицы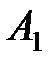 
, 
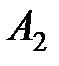и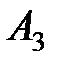 
– объемы продаж этой продукции в магазинах в первом, втором и третьем месяцах соответственно (усл. ед.). Цена реализации одной условной единицы первого и второго вида масла задана матрицей 
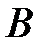(ден. ед.). Определить:
1) матрицу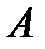 
- объем продаж за квартал;
2) прирост продаж за каждый месяц по сравнению с предыдущим;
3) выручку каждого магазина за квартал.
Проанализировать результаты.
Вариант 1.
, 
, 
, 
.
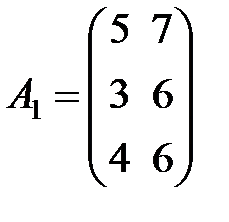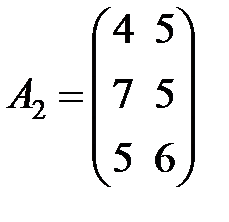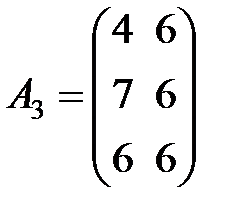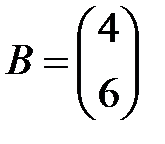Вариант 2.
, 
, 
, 
.
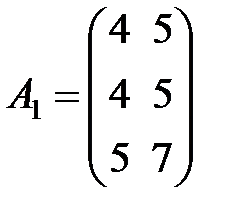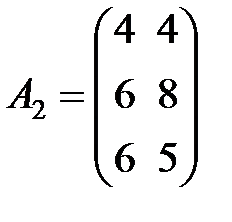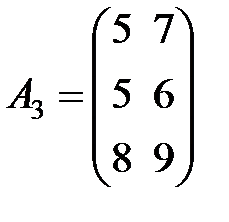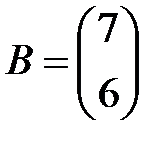Вариант 3.
, 
, 
, 
.
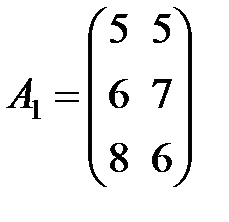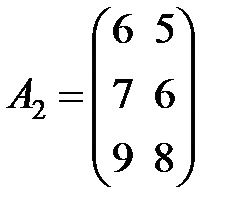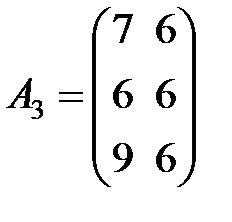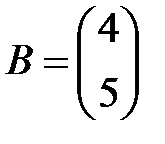Вариант 4.
, 
, 
, 
.
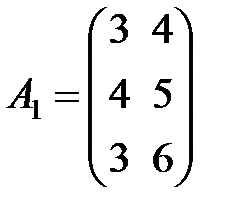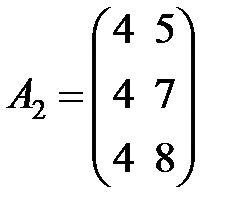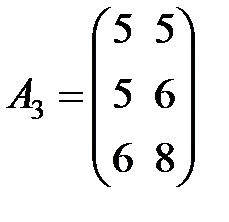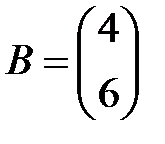Вариант 5.
, 
, , 
.
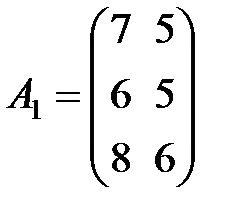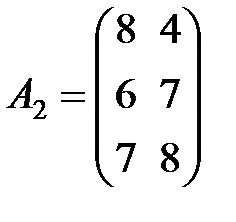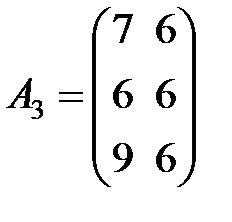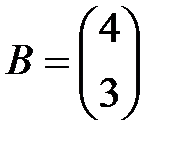Вариант 6.
, , , 
.
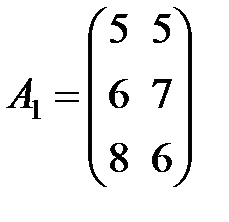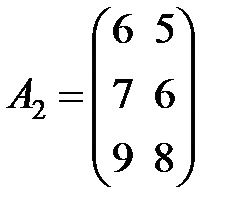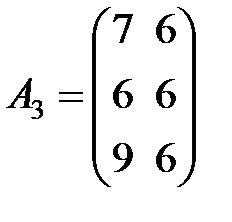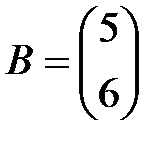Вариант 7.
, 
, 
, 
.
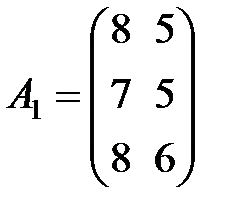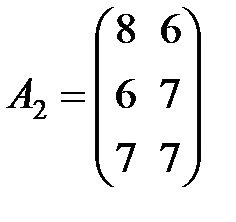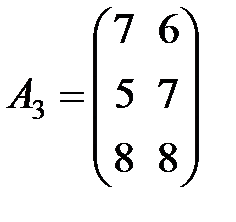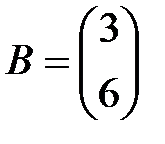Вариант 8.
, 
, 
, 
.
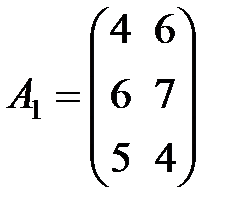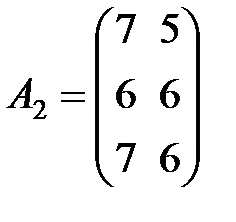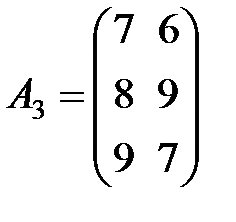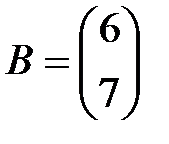Вариант 9.
, 
, 
, 
.
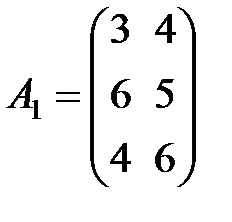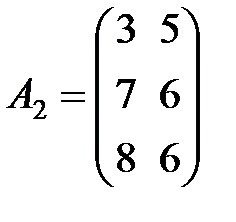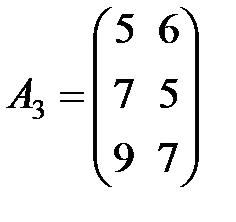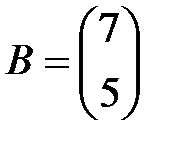Вариант 10.
, 
, 
, 
.
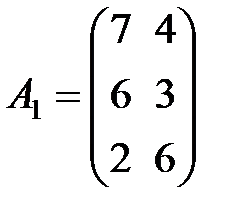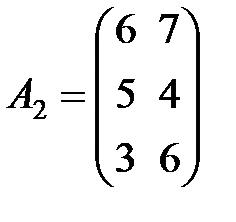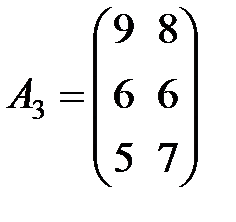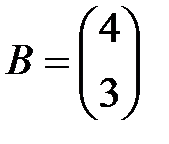Вариант 11.
, , , .
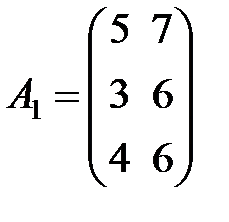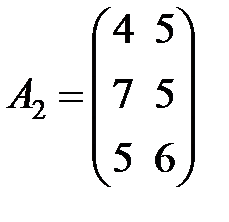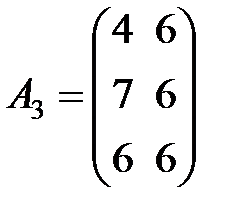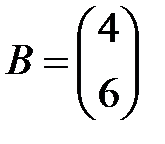Вариант 12.