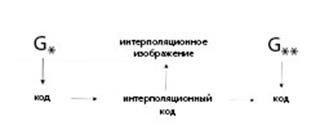
Интерполяция изображений на основе кодов IFS

Поскольку изображения хранятся обычно в сжатом (фактически закодированном) виде, то вполне логично было бы строить интерполяционные изображения на основе имеющейся информации, то есть кодов. К сожалению, такой метод не может быть универсальным, то есть не может давать в каждой ситуации хорошие результаты. Это связано с тем, что кодирование – нелинейный процесс, и, как следствие, трудно подобрать подходящий метод интерполяции кодов.

Тем не менее, подход с кодами к решению задачи об интерполяции изображений имеет место. Рассмотрим процесс на примере кодирования ранее изученным методом IFS.

Пусть есть два множества (изображения), заданные (кодируемые) при помощи наборов преобразований:

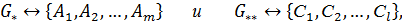
где преобразования имеют общий вид:

.

Для начала, будем считать, что 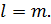Каждому аффинному преобразованию, из кода изображения сопоставим некоторое преобразование из кода изображения : .

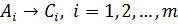Коэффициенты преобразований могут быть записаны в виде векторов из R⁶. Поэтому каждую пару преобразований ( векторов) можно проинтерполиро-вать, например, по формуле Минковского. Таким образом, при каждом

значении 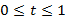получаем набор переходных аффинных преобразований ,

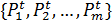где

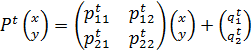
Именно этот полученный набор аффинных преобразований мы и принимаем за код интерполяционного изображения.

Рассмотрим пример работы описанного алгоритма.

Пусть заданы два прямоугольника (квадрата) и (рис. 16).

Построим по ним промежуточное (интерполяциионное) изображение (в смысле интерполяции на основе кодов).

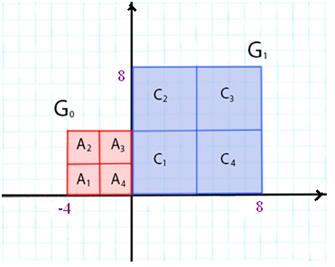
Сначала для 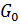и 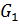найдём преобразования, кодирующие их методом IFS:

,

, ;

,

. .

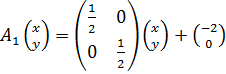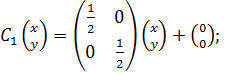
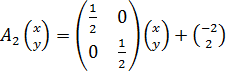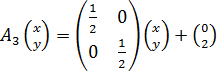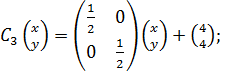
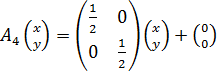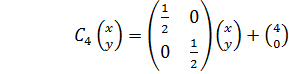По этим наборам строим набор интерполяционных преобразований.

При 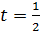для каждой пары преобразований вычисляем переходное преобразование 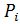. Получим, что интерполяционный код имеет следующий вид (ясно, что изменятся только «векторы сдвига») :

;

.

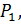
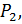
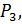
Найти изображение, соответствующее (коду) набору 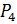( 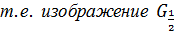в смысле интерполяции на основе кодов), можно путём итераций преобразования 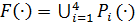– при любом выборе начального изображения, последовательность изображений 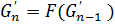будет сходиться по метрике Хаусдорфа к .

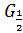Однако логично проверить, не будет ли этим изображением 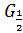квадрат (который получился бы методом Минковского) со стороной 6, имеющий с осью абсцисс общий отрезок 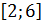(см. рис. 17).

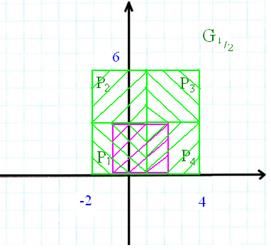
Закодировав обсуждаемый квадрат методом IFS, мы получим в качестве его кода именно набор преобразований 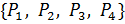, т.е. квадрат и является изображением 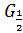в смысле интерполяции на основе кодов. /На рисунке для наглядности фиолетовым цветом представлено сжатое в 2 раза относительно начала координат изображение ./

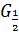Таким образом, при выполнении определённых правил, результат интерполяции на основе кодов получается вполне приемлемым.

Если в кодах IFS получается, например, 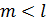. Тогда в наборе 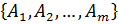продублируем некоторые преобразования, чтобы количество их стало равным :

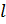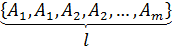
Очевидно, что множество 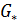по-прежнему кодируется этим набором (является объединением уменьшенных образов). После такого пополнения набора преобразований, мы действуем дальше как в случае, когда .

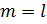Аналогично решается ситуация, когда .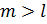

Главная сложность при интерполяции на основе кодов IFS – это правильный подбор пар интерполяционных аффинных преобразований. Другой трудностью является то, что матрица, являющаяся интерполяционной между двумя заданными, обладающими свойством сжатия, может таким свойством не обладать. Это объясняется тем, что величина собственных значений не выражается линейно через коэффициенты матрицы.