Исходные и расчетные данные для определения коэффициента полной регрессии по выборке крупных и средних организаций
| Номер хозяйства | Урожайность зерновых и зернобобовых, ц/га | Затраты на минеральные удобрения в расчете на 1 га убранной площади, тыс. руб. | Отклонение от средних значений | Квадраты отклонений | Отношение отклонений от средних значений | Взвешенное отношение отклонений от средних значений | ||
| у | х | 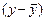 | 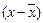 | 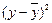 | 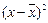 | 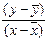 | 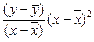 | |
| 14,96 | 0,97 | -11,96 | -0,58 | 143,01 | 0,33 | 20,75 | 6,89 | |
| 20,15 | 0,27 | -6,77 | -1,28 | 45,79 | 1,63 | 5,30 | 8,64 | |
| 20,65 | 0,92 | -6,27 | -0,63 | 39,29 | 0,40 | 9,88 | 3,98 | |
| 20,71 | 1,21 | -6,21 | -0,34 | 38,57 | 0,12 | 18,25 | 2,11 | |
| 20,89 | 0,81 | -6,03 | -0,74 | 36,36 | 0,55 | 8,15 | 4,46 | |
| 21,65 | 0,48 | -5,27 | -1,07 | 27,73 | 1,14 | 4,94 | 5,62 | |
| 22,23 | 0,38 | -4,69 | -1,17 | 21,97 | 1,38 | 4,00 | 5,50 | |
| 22,95 | 1,29 | -3,97 | -0,26 | 15,78 | 0,07 | 15,27 | 1,03 | |
| 23,78 | 0,74 | -3,14 | -0,81 | 9,86 | 0,66 | 3,87 | 2,55 | |
| 24,34 | 2,11 | -2,58 | 0,56 | 6,64 | 0,31 | -4,60 | -1,44 | |
| 25,75 | 0,61 | -1,17 | -0,94 | 1,37 | 0,89 | 1,24 | 1,10 | |
| 26,05 | 1,02 | -0,87 | -0,53 | 0,75 | 0,29 | 1,62 | 0,46 | |
| 26,25 | 1,36 | -0,67 | -0,19 | 0,44 | 0,04 | 3,43 | 0,13 | |
| 27,24 | 0,47 | 0,32 | -1,08 | 0,10 | 1,17 | -0,29 | -0,34 | |
| 28,49 | 1,11 | 1,57 | -0,44 | 2,45 | 0,19 | -3,57 | -0,69 | |
| 28,66 | 2,33 | 1,74 | 0,78 | 3,02 | 0,61 | 2,23 | 1,36 | |
| 29,66 | 4,08 | 2,74 | 2,53 | 7,53 | 6,39 | 1,09 | 6,94 | |
| 30,67 | 2,00 | 3,75 | 0,45 | 14,05 | 0,20 | 8,34 | 1,68 | |
| 32,31 | 3,43 | 5,39 | 1,88 | 29,10 | 3,52 | 2,87 | 10,12 | |
| 32,54 | 2,16 | 5,62 | 0,61 | 31,61 | 0,37 | 9,22 | 3,43 | |
| 36,45 | 2,58 | 9,53 | 1,03 | 90,82 | 1,07 | 9,23 | 9,84 | |
| 40,71 | 2,41 | 13,80 | 0,85 | 190,30 | 0,73 | 16,14 | 11,79 | |
| 42,04 | 2,93 | 15,12 | 1,38 | 228,70 | 1,89 | 10,99 | 20,81 | |
| Итого | 619,13 | 35,66 | х | х | 985,24 | 23,93 | х | 105,96 |
Он показывает, что при увеличении затрат на минеральные удобрения в расчете на 1 га посевной площади на 1 тысячу рублей, урожайность в данной совокупности возрастает в среднем на 4,43 ц/га.
4. Задачами корреляционного анализа являются оценка тесноты связи между изучаемыми признаками и ее достоверности. В целях сопоставимости показателей для разных моделей, изучающих связи разноименных величин, переходят от индивидуальных отклонений (1.13) к преобразованным – нормированным отклонениям t:
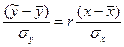 1.15
1.15
или 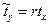 , 1.16
, 1.16
где коэффициент пропорциональности уже не b, а r – коэффициент парной линейной корреляции, отсюда:
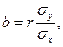 1.17
1.17
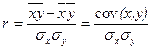 . 1.18
. 1.18
Исходя из (1.15) коэффициент корреляции показывает, на сколько среднеквадратических отклонений изменится y, если х изменится на одно свое среднеквадратическое отклонение.
Вследствие неравенства Коши-Буняковского 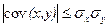 , коэффициент парной линейной корреляции изменяется в пределах
, коэффициент парной линейной корреляции изменяется в пределах 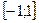 , в случае если он равен по модулю единице, то речь идет о функциональной связи, нулю – об отсутствии связи. Знак коэффициента корреляции, который всегда совпадает со знаком коэффициента полной регрессии, исходя из (1.17), указывает на направление связи: прямую (при положительном r) и обратную (при отрицательном). Оценка тесноты (силы) связи проводится на основе значения коэффициента корреляции, взятого по модулю:
, в случае если он равен по модулю единице, то речь идет о функциональной связи, нулю – об отсутствии связи. Знак коэффициента корреляции, который всегда совпадает со знаком коэффициента полной регрессии, исходя из (1.17), указывает на направление связи: прямую (при положительном r) и обратную (при отрицательном). Оценка тесноты (силы) связи проводится на основе значения коэффициента корреляции, взятого по модулю: 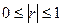 ; чем выше коэффициент корреляции, тем сильнее связь между переменными.
; чем выше коэффициент корреляции, тем сильнее связь между переменными.
Для коэффициентов корреляции разработаны шкалы меры тесноты связи. В практических исследованиях часто ориентируются на следующий вариант шкалы:
до 0,3 – связь практически отсутствует,
0,3-0,5 – связь слабая,
0,5-0,7 – связь умеренная (средняя),
0,7- 0,9 – связь тесная (сильная),
0,9-0,99 – связь очень тесная (близка к функциональной).
Уравнение (1.16) называют стандартизованным уравнением регрессии, где в качестве переменных выступают нормированные отклонения, а параметрами – стандартизованные коэффициенты регрессии (бета-коэффициенты), так для двухфакторной модели:
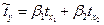 , 1.19
, 1.19
где 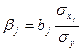 , 1.20
, 1.20
для парной линейной модели 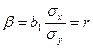 .
.
Из уравнения (1.16) следует, что коэффициент корреляции для каждого отдельного наблюдения равен:
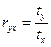 , 1.21
, 1.21
откуда следует, что 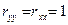 .
.
Для нахождения среднего коэффициента корреляции, как и b (1.14), необходимо произвести взвешивание:
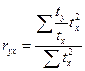 , 1.22
, 1.22
учитывая, что 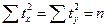
(действительно: 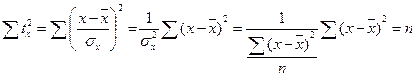 ),
),
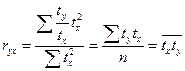 , 1.23
, 1.23
т.е. форма средней простой произведения нормированных отклонений равнозначна средней взвешенной этих же отношений.
По данным таблицы 1.1 рассчитаем нормированные отклонения, их произведения и отношения (табл. 1.2).
Таблица 1.2
Нормированные отклонения
| Номер хозяйства | Урожайности, 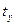 | Затрат на минеральные удобрения, 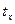 | Квадрат | Отношение | Взвешенное отношение/произведение |
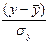 | 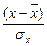 | 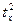 | 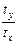 | 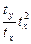 = = 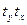 | |
| -1,83 | -0,57 | 0,32 | 3,23 | 1,03 | |
| -1,03 | -1,25 | 1,57 | 0,83 | 1,29 | |
| -0,96 | -0,62 | 0,39 | 1,54 | 0,60 | |
| -0,95 | -0,33 | 0,11 | 2,84 | 0,32 | |
| -0,92 | -0,72 | 0,53 | 1,27 | 0,67 | |
| -0,80 | -1,05 | 1,09 | 0,77 | 0,84 | |
| -0,72 | -1,15 | 1,32 | 0,62 | 0,82 | |
| -0,61 | -0,26 | 0,07 | 2,38 | 0,15 | |
| -0,48 | -0,79 | 0,63 | 0,60 | 0,38 | |
| -0,39 | 0,55 | 0,30 | -0,72 | -0,22 | |
| -0,18 | -0,92 | 0,85 | 0,19 | 0,16 | |
| -0,13 | -0,52 | 0,27 | 0,25 | 0,07 | |
| -0,10 | -0,19 | 0,04 | 0,54 | 0,02 | |
| 0,05 | -1,06 | 1,12 | -0,05 | -0,05 | |
| 0,24 | -0,43 | 0,19 | -0,56 | -0,10 | |
| 0,27 | 0,77 | 0,59 | 0,35 | 0,20 | |
| 0,42 | 2,48 | 6,14 | 0,17 | 1,04 | |
| 0,57 | 0,44 | 0,19 | 1,30 | 0,25 | |
| 0,82 | 1,84 | 3,39 | 0,45 | 1,52 | |
| 0,86 | 0,60 | 0,36 | 1,44 | 0,51 | |
| 1,46 | 1,01 | 1,02 | 1,44 | 1,47 | |
| 2,11 | 0,84 | 0,70 | 2,52 | 1,77 | |
| 2,31 | 1,35 | 1,82 | 1,71 | 3,12 | |
| Итого | - | - | 23,00 | х | 15,87 |
Коэффициент парной линейной корреляции будет равен: 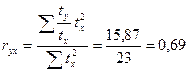 , что свидетельствует о достаточно тесной связи между затратами на минеральные удобрения и урожайностью зерновых и зернобобовых по выборке хозяйств Белгородской области.
, что свидетельствует о достаточно тесной связи между затратами на минеральные удобрения и урожайностью зерновых и зернобобовых по выборке хозяйств Белгородской области.
