Оптика и физика твердого тела
ОСНОВНЫЕ ФОРМУЛЫ И ЗАКОНЫ
| Физическая величина или закон | Формула |
| Показатель преломления среды | 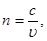 где n – показатель преломления среды, с - скорость распространения света в вакууме, где n – показатель преломления среды, с - скорость распространения света в вакууме, 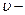 скорость распространения света в среде скорость распространения света в среде |
| Оптическая длина пути луча | L=n l, где L – оптическая длина пути луча, n – показатель преломления среды, l – геометрическая длина луча |
| Оптическая разность хода волн | 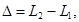 где ∆ - оптическая разность хода волн, L – оптическая длина пути луча где ∆ - оптическая разность хода волн, L – оптическая длина пути луча |
| Условие максимума (усиления) света при интерференции | 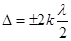 , k =0,1,2,3…, где ∆ - оптическая разность хода, λ – длина волны , k =0,1,2,3…, где ∆ - оптическая разность хода, λ – длина волны |
| Условие минимума (ослабления) света при интерференции | 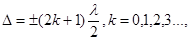 где ∆ - оптическая разность хода, λ – длина волны где ∆ - оптическая разность хода, λ – длина волны |
| Линейное и угловое расстояния между соседними интерференционными полосами на экране | 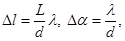 где L – оптическая длина пути луча, l – линейное расстояние между полосами на экране, λ – длина волны, d – расстояние между источниками, ∆λ – угловое расстояние между полосами на экране где L – оптическая длина пути луча, l – линейное расстояние между полосами на экране, λ – длина волны, d – расстояние между источниками, ∆λ – угловое расстояние между полосами на экране |
| Оптическая разность хода волн в тонких пленках в отраженном и проходящем свете | 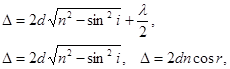 где ∆ - оптическая разность хода, λ – длина волны, d – толщина, n – показатель преломления среды, i – угол падения волны, r — угол преломления где ∆ - оптическая разность хода, λ – длина волны, d – толщина, n – показатель преломления среды, i – угол падения волны, r — угол преломления |
| Разрешающая сила дифракционной решетки | 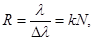 где R - разрешающая сила дифракционной решетки, λ – длина волны, N — число штрихов решетки, ∆λ – изменение длины волны, k — порядковый номер дифракционного максимума где R - разрешающая сила дифракционной решетки, λ – длина волны, N — число штрихов решетки, ∆λ – изменение длины волны, k — порядковый номер дифракционного максимума |
| Световой поток Ф, испускаемый изотропным источником в пределах телесного угла ω | Ф = I ω, где Ф – световой поток, ω – телесный угол, I – сила света |
| Освещенность поверхности | E = Ф / S, где Е – освещенность поверхности, Ф – световой поток, S – площадь поверхности |
| Освещенность, создаваемая изотропным источником света | 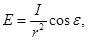 где Е – освещенность поверхности, I – сила света источника, ε — угол падения лучей, r — расстояние от поверхности до источника света где Е – освещенность поверхности, I – сила света источника, ε — угол падения лучей, r — расстояние от поверхности до источника света |
| Яркость светящейся поверхности | В = I / ΔS, где В – яркость, I – сила света, |
| Светимость поверхности | R = Ф / S, где R – светимость поверхности, Ф – световой поток, S – площадь поверхности |
| Светимость косинусных излучателей | R = π B, где R – светимость, В – яркость |
| Условие главных максимумов дифракционной решетки | 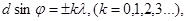 где d– период дифракционной решетки, k – порядок главного максимума, φ - угол дифракции, λ – длина волны где d– период дифракционной решетки, k – порядок главного максимума, φ - угол дифракции, λ – длина волны |
| Условие дифракционных максимумов от одной щели | 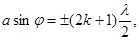 где α – ширина щели, k – порядок максимума, λ – длина волны, φ - угол дифракции где α – ширина щели, k – порядок максимума, λ – длина волны, φ - угол дифракции |
| Условие дифракционных минимумов от одной щели | 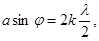 где α – ширина щели, k – порядок минимума, λ – длина волны, φ - угол дифракции где α – ширина щели, k – порядок минимума, λ – длина волны, φ - угол дифракции |
| Закон Брюстера | 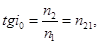 где где 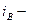 угол падения, n2, n1 –показатели преломления первой и второй среды. угол падения, n2, n1 –показатели преломления первой и второй среды. |
| Закон Малюса | 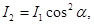 где I1 – интенсивность света, падающего на анализатор, I2 – интенсивность света, вышедшего из анализатора, α – угол между плоскостями поляризатора и анализатора где I1 – интенсивность света, падающего на анализатор, I2 – интенсивность света, вышедшего из анализатора, α – угол между плоскостями поляризатора и анализатора |
| Формула Вульфа-Брегга | 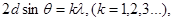 где d – расстояние между атомными плоскостями кристалла, θ – угол скольжения, λ – длина волны где d – расстояние между атомными плоскостями кристалла, θ – угол скольжения, λ – длина волны |
| Угол вращения плоскости поляризации в кристаллах и растворах | 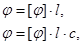 где φ - угол вращения плоскости поляризации, l – длина пути света в оптически активном веществе, с – скорость света где φ - угол вращения плоскости поляризации, l – длина пути света в оптически активном веществе, с – скорость света |
| Закон Стефана-Больцмана | 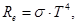 где Re – энергетическая светимость, σ – постоянная Стефана-Больцмана, Т - температура где Re – энергетическая светимость, σ – постоянная Стефана-Больцмана, Т - температура |
| Закон смещения Вина | 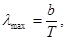 где λmax – длина волны с максимальным значением спектральной плотности энергетической светимости черного тела, b – постоянная Вина, Т - температура где λmax – длина волны с максимальным значением спектральной плотности энергетической светимости черного тела, b – постоянная Вина, Т - температура |
| Энергия фотона | 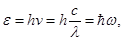 где h – постоянная Планка, ν – частота, λ – длина волны, с – скорость света, где h – постоянная Планка, ν – частота, λ – длина волны, с – скорость света, 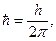 ω – частота излучения ω – частота излучения |
| Импульс фотона | 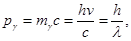 где где 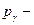 импульс фотона, импульс фотона, 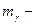 масса фотона, с – скорость света, h – постоянная Планка, ν – частота, λ – длина волны масса фотона, с – скорость света, h – постоянная Планка, ν – частота, λ – длина волны |
| Давление света при нормальном падении | 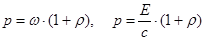 |
| Уравнение Эйнштейна для внешнего фотоэффекта | hv=A+T, где h – постоянная Планка, ν – частота излучения, А – работа выхода, T – кинетическая энергия фотоэлектрона |
| при T < 5 кэВ | 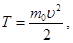 где T – кинетическая энергия электрона, где T – кинетическая энергия электрона, 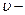 скорость электрона, т0 – масса покоя электрона скорость электрона, т0 – масса покоя электрона |
| при T > 5 кэВ | 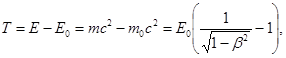 где T – кинетическая энергия, т0 – масса покоя электрона, т – масса электрона, Е – энергия электрона, Е0 –энергия покоя электрона, где T – кинетическая энергия, т0 – масса покоя электрона, т – масса электрона, Е – энергия электрона, Е0 –энергия покоя электрона, 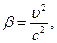 т0 – масса покоя электрона т0 – масса покоя электрона |
| Изменение длины волны при эффекте Комптона | 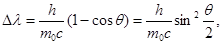 где ∆λ – изменение длины волны, h – постоянная Планка, с – скорость света, θ – угол рассеивания фотона, т0 – масса электрона отдачи где ∆λ – изменение длины волны, h – постоянная Планка, с – скорость света, θ – угол рассеивания фотона, т0 – масса электрона отдачи |
| Формула Бальмера | 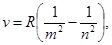 где ν – частота испускаемого света, R - постоянная Ридберга, n, m - номера орбит электрона(m=1,2,3…), (n=m+1) где ν – частота испускаемого света, R - постоянная Ридберга, n, m - номера орбит электрона(m=1,2,3…), (n=m+1) |
| Момент импульса электрона на стационарных орбитах | 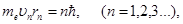 где где 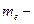 масса электрона, масса электрона, 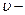 скорость электрона, скорость электрона, 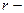 радиус орбиты радиус орбиты |
| Второй постулат Бора | 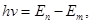 где h – постоянная Планка, ν – частота испускаемого света, En – энергия атома до излучения/поглощения, Em - энергия атома после излучения/поглощения где h – постоянная Планка, ν – частота испускаемого света, En – энергия атома до излучения/поглощения, Em - энергия атома после излучения/поглощения |
| Соотношения неопределенностей |  где ∆х – неопределенность координаты микрочастицы, ∆р - соответствующая координате неопределенность проекции импульса, h – постоянная Планка, ∆Е – неопределенность энергии некоторого состояния системы, ∆t - время где ∆х – неопределенность координаты микрочастицы, ∆р - соответствующая координате неопределенность проекции импульса, h – постоянная Планка, ∆Е – неопределенность энергии некоторого состояния системы, ∆t - время |
| Длина волны де Бройля | 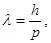 где λ – длина волны, h – постоянная Планка, р – импульс микрочастицы где λ – длина волны, h – постоянная Планка, р – импульс микрочастицы |
| Стационарное уравнение Шредингера | 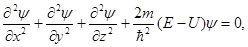 где ψ – волновая функция частицы, где ψ – волновая функция частицы, 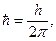 h – постоянная Планка, U – потенциальная функция частицы в силовом поле, Е – энергия частицы, x,y,z – координаты частицы, т – масса частицы, h – постоянная Планка, U – потенциальная функция частицы в силовом поле, Е – энергия частицы, x,y,z – координаты частицы, т – масса частицы, 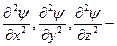 вторые частные производные волновой функции по координатам вторые частные производные волновой функции по координатам |
| Вероятность обнаружения частицы в интервале от x1 до x2 | 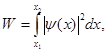 где W – вероятность, ψ – волновая функция частицы где W – вероятность, ψ – волновая функция частицы |
| Собственное значение энергии En частицы, находящейся на n-ом энергетическом уровне в бесконечно глубоком одномерном потенциальном ящике | 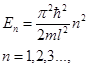 где где 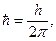 h – постоянная Планка, т – масса частицы, n – главное квантовое число, l – орбитальное квантовое число h – постоянная Планка, т – масса частицы, n – главное квантовое число, l – орбитальное квантовое число |
| Соответствующая этой энергии собственная волновая функция имеет вид | 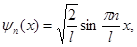 где ψ – волновая функция частицы, n – главное квантовое число, l - орбитальное квантовое число, х - координата частицы где ψ – волновая функция частицы, n – главное квантовое число, l - орбитальное квантовое число, х - координата частицы |
| Коэффициенты отражения ρ и пропускания τ волн де Бройля через низкий (U < E) потенциальный барьер бесконечной ширины | 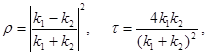 где где 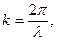 λ – длина волны λ – длина волны |
| Коэффициент прозрачности D прямоугольного потенциального барьера конечной ширины | 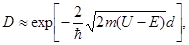 где U – высота потенциального барьера, т – масса частицы, где U – высота потенциального барьера, т – масса частицы, 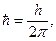 h – постоянная Планка, Е – энергия частицы h – постоянная Планка, Е – энергия частицы |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
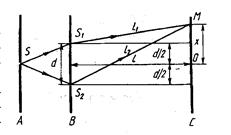 Задача 1.В опыте Юнга источником света служит ярко освещенная узкая щель S в экране А (Рис. 26). Свет от нее падает на второй непрозрачный экран В, в котором имеются две щели S1 и S2, находящемся на расстоянии d = 0,2 мм друг от друга. Интерференция наблюдается на экране С, параллельном экрану В и расположенном от него на расстоянии l = 2 м. найти расстояние между двумя соседними максимумами, если длина световой волны
Задача 1.В опыте Юнга источником света служит ярко освещенная узкая щель S в экране А (Рис. 26). Свет от нее падает на второй непрозрачный экран В, в котором имеются две щели S1 и S2, находящемся на расстоянии d = 0,2 мм друг от друга. Интерференция наблюдается на экране С, параллельном экрану В и расположенном от него на расстоянии l = 2 м. найти расстояние между двумя соседними максимумами, если длина световой волны
λ = 500 нм. Рис. 26
Интерференционная картина представляет собой чередование светлых и темных полос (максимумов и минимумов), параллельных друг другу. В некоторой точке М экрана С будет наблюдаться максимум при вы полнении условия
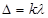 , (1)
, (1)
где 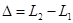 - оптическая разность хода. В данном случае
- оптическая разность хода. В данном случае 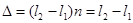 , т.к. показатель преломления воздуха n = 1.
, т.к. показатель преломления воздуха n = 1.
Обозначим через xk расстояние от точки М до точки О, симметричной относительно щелей. Из рисунка видно, что
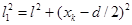 ,
, 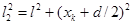
Вычтем из одного уравнение другое и раскроем квадрат разности и квадрат суммы, получим:
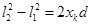 ,
,
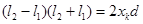 .
.
Т.к.l »d, то 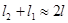 , а
, а 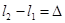 , поэтому
, поэтому
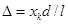 . (2)
. (2)
Подставив значение Δ из равенства (1) в (2), найдем
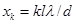 .
.
Расстояние Δx между двумя соседними интерференционными максимумами
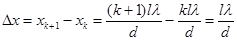 .
.
Выполним анализ размерности:
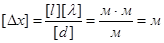
Подставив числовые значения получим 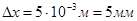 .
.
Отметим, что величина 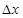 называется шириной интерференционной полосы.
называется шириной интерференционной полосы.
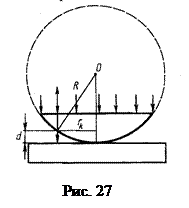
Задача 2. Кольца Ньютона образуются в прослойке воздуха между плоскопараллельной стеклянной пластинкой и положенной на нее плосковыпуклой линзой с радиусом кривизны R = 5 м. Наблюдение ведется в отраженном свете. Радиус третьего темного кольца r3 = 3,1 мм. Найти длину волны света, падающего нормально на плоскую поверхность линзы.
Решение. В отраженном свете темные кольца образуются при выполнении условия интерференционных минимумов
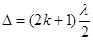 (k = 0, 1, 2, …), (1)
(k = 0, 1, 2, …), (1)
где Δ – оптическая разность хода волн, отраженных от выпуклой поверхности на границе раздела стекло-воздух и от пластинки на границе воздух-стекло. Во втором случае отражение происходит от оптически более плотной среды, поэтому теряется половина волны. С учетом этого находим, что разность хода
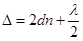 , (2)
, (2)
где d – толщина воздушного зазора, n – показатель преломления
 воздуха (n = 1).
воздуха (n = 1).
Из рисунка 27 видно, что
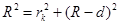 , или
, или 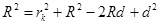 .
.
Отсюда, учитывая, что d « R, получим
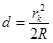 .
.
Подставив это значение d и n = 1 в формулу (2), получим
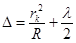 . (3)
. (3)
Приравняв правые части выражений (1) и (3), будем иметь формулу радиуса k-го темного кольца Ньютона в отраженном свете:
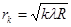 (k = 0, 1, 2, …).
(k = 0, 1, 2, …).
Отсюда найдем длину световой волны:
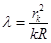 .
.
Следовательно,
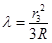 , λ = 6,4·10-7 м.
, λ = 6,4·10-7 м.
Задача 3. На узкую щель шириной a = 0,55 мм падает нормально монохроматический свет с длиной волны λ = 694 нм. Определите направление луча света на вторую светлую дифракционную полосу (по отношению к первоначальному направлению света).
Решение. Запишем формулу условия максимума для дифракции Фраунгофера на одной щели
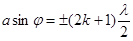 . (1)
. (1)
В условии нашей задачи необходимо определить направление света - следовательно, мы должны найти угол, под которым падает свет на вторую дифракционную полосу k = 2.
Подставляем значение k = 2 в выражение (1) и получаем значение синуса угла падения на вторую светлую дифракционную полосу
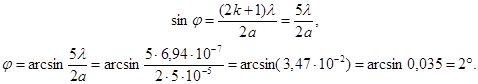
Задача 4. Степень поляризации частично поляризованного света составляет 0,75. Определите отношение максимальной интенсивности света, пропускаемого анализатором, к минимальной.
Решение. По условию задачи степень поляризации P = 0,75. Она определяется согласно следующему отношению максимальной и минимальной интенсивности света
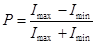
Из этого выражения нам необходимо выразить отношение Imax / Imin
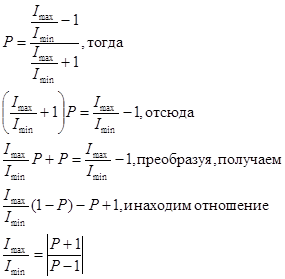
Подставим значения P = 0,75 и получим, что отношение Imax / Imin =7.
Задача 5. Люминесцентная цилиндрическая лампа диаметром d = 2,5 см и длиной l = 40 см создает на расстоянии r = 5 м в направлении, перпендикулярном оси лампы, освещенность E = 2 лк. Принимая лампу за косинусный излучатель, определить: 1) силу света I в данном направлении; 2) яркость В; 3) светимость R лампы.
Решение. 1) Больший из двух размеров лампы – длина в 12 раз меньше расстояния, на котором измерена освещенность. Следовательно, для вычисления силы света в данном направлении можно принять лампу за точечный источник и применить формулу
E = I / r2,
откуда
I = E r2.
Подставив значения величин в эту формулу, и произведя вычисления, получим I = 25 кд.
2) Для вычисления яркости применим формулу
В = I / σ.
Где σ – площадь проекции протяженного источника света на плоскость, перпендикулярную направлению наблюдения.
В случае цилиндрической люминесцентной лампы проекция имеет форму прямоугольника длиной l и шириной d. Следовательно,
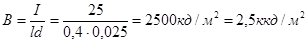
3) Так как люминесцентную лампу можно считать косинусным излучателем, то ее светимость
R = π • B=7,9 клк.
Задача 6. Определите, во сколько раз изменится мощность излучения черного тела, если длина волны, соответствующая максимуму его спектральной плотности энергетической светимости сместилась с λ1 = 720 нм до λ2 = 400 нм.
Решение. Для решения этой задачи запишем закон смещения Вина для первой и второй длины волны.
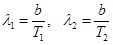 (1)
(1)
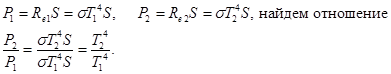 Запишем значение мощности излучения для каждого случая и найдем их отношение. Мощность излучения связана с энергетической светимостью черного тела следующим соотношением
Запишем значение мощности излучения для каждого случая и найдем их отношение. Мощность излучения связана с энергетической светимостью черного тела следующим соотношением
Необходимые значения температур Т1 и Т2 выражаем из соотношений (1) и получаем необходимое отношение мощностей Р2 и Р1
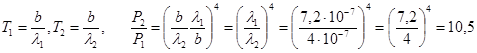
Задача 7. Фотоэлектроны, вырываемые с поверхности металла, полностью задерживаются при приложении обратного напряжения Uо = 3 В. Фотоэффект для этого металла начинается при частоте падающего монохроматического света vо = 6•1016 c-1. Определите 1) работу выхода электронов из металла; 2) частоту применяемого излучения.
Решение. Запишем уравнение Эйнштейна для внешнего фотоэффекта.
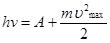 (1)
(1)
Максимальная кинетическая энергия электронов равна произведению заряда электрона на величину задерживающего напряжения. Подставляя ее значение в выражение (1) найдем работу выхода электронов из металла.
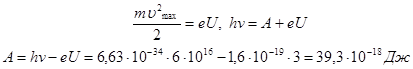
Частота применяемого излучения определяется по формуле Эйнштейна при условии, что кинетическая энергия электронов будет равна нулю.
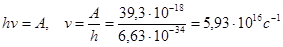
Задача 8. Калий освещается монохроматическим светом с длиной волны λ = 400 нм. Определите наименьшее задерживающее напряжение, при котором фототок прекратится. Работа выхода электронов из калия равна 2,2 эВ.
Решение. Запишем уравнение Эйнштейна для фотоэффекта, и укажем, что максимальная кинетическая энергия электронов определяется произведением заряда электрона на величину задерживающего напряжения.
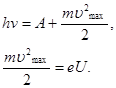
В нашем случае дана частота, которая связана с длиной волны следующим соотношением v = c / λ. Подставляя необходимые значения в формулу Эйнштейна для внешнего фотоэффекта, получим значение задерживающего напряжения. Учитывая, что
А = 2,2 эВ = 2,2•1,6•10-19 Дж = 3,52•10-19 Дж.
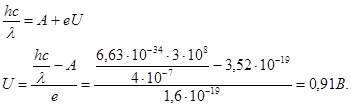
Задача 9.Определите энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на второй.
Решение. Обозначим энергию фотона, испускаемого атомом водорода при переходе электрона с третьего уровня на второй
E 3,2 = h v3,2. (1)
Для того, чтобы определить частоту испускаемого излучения воспользуемся формулой Бальмера.
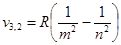 .(2)
.(2)
Согласно условию задачи m = 2, n = 3. Подставляя выражение (2) в уравнение (1), и используя значения постоянной Ридберга R = 3,29•1015 c-1, значения m и n, находим энергию испускаемого фотона.
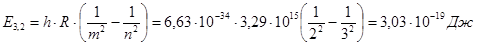
Полученное значение энергии фотона переводим из единиц измерения в джоулях в значение в электрон-вольтах.
Поскольку 1эВ = 1,6•10-19 Дж, то
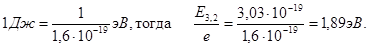
Задача 10.Определите скорость υ электрона на третьей орбите атома водорода.
Решение. На электрон, движущийся по орбите, действует сила Кулона. В атоме водорода заряд ядра равен заряду электрона, поэтому величина силы Кулона определяется по формуле
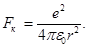 (1)
(1)
Согласно второму закону Ньютона, произведение массы на ускорение равно сумме всех сил, действующих не тело. На электрон действует только сила Кулона, поэтому
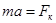 (2)
(2)
Ускорение при равномерном движении электрона по орбите будет направлено к центру, и определяется по формуле
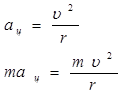
(3)
Подставим в выражение (2) значение центростремительного ускорения (3) и значение силы Кулона и выразим радиус орбиты электрона
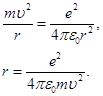 (4)
(4)
Найденный радиус орбиты электрона потребуется нам для того, чтобы определить скорость движения электрона по орбите из формулы для момента импульса электрона на стационарной орбите:
m υ r = n ћ. (5)
Подставим в выражение (5) значение радиуса орбиты электрона, значение n = 3 (третья орбита) и выразим скорость движения электрона по орбите

Задача 11.Определите длину волны де Бройля для электрона, находящегося в атоме водорода на третьей боровской орбите.
Решение. Длина волны де Бройля определяется по формуле
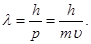
(1)
Скорость электрона на третьей боровской орбите определим из формулы для момента импульса электрона на стационарной орбите
m υ r = n ћ. (2)
В этой формуле нам неизвестен радиус, который мы можем выразить из второго закона Ньютона так же, как и в Задаче № 9, см. формулу (4)
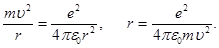 (3)
(3)
Мы получили два уравнения с двумя неизвестными. Выразим из выражения (2) радиус и приравняем его с уравнением (3)
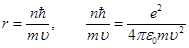 (4)
(4)
Из полученного соотношения выразим скорость, подставим ее значение в выражение (1) и учтем, что 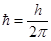
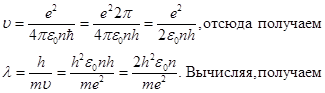
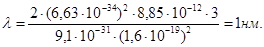
Задача 12. Используя теорию Бора, определите орбитальный магнитный момент электрона, движущегося по третьей орбите атома водорода.
Решение. Магнитный момент определяется по формуле
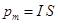 (1)
(1)
где I – сила тока, S – площадь контура, по которому протекает ток.
Согласно определению сила тока I = Δ q /Δ t – отношение заряда ко времени. Величина эквивалентного тока, создаваемого в атоме при орбитальном движении одной зараженной частицы (электрона) будет определяться как отношение заряда электрона к периоду его обращения по орбите.
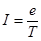 (2)
(2)
Период определяем через скорость движения электрона по орбите. Скорость движения определяется как отношение длины окружности, по которой движется электрон к периоду его обращения. Отсюда выражаем период обращения электрона:
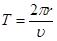 (3)
(3)
Площадь круга, описываемая электроном при движении по орбите равна
S = π r 2. (4)
Подставляя необходимые значения в формулу (1) получаем значение искомого магнитного момента электрона
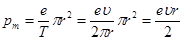 . (5)
. (5)
В данном выражении присутствуют две неизвестных величины – скорость и радиус орбиты электрона. Согласно условию, электрон движется по третьей орбите атома водорода, следовательно, можно определить неизвестное произведение скорости и радиуса орбиты электрона из формулы для момента импульса электрона
m υ r = n ћ. (6)
и выразим из него произведение υ r
υ r = n ћ / m. (7)
подставим выражение (7) в выражение (5) и получим значение орбитального магнитного момента
pm = e n ћ / 2 m,
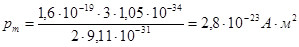
Задача 13.Определите из соотношения неопределенностей скорости электрона, если его координата установлена с точностью до Δ x =10-5 м, и пылинки массой m = 10-12 кг, если ее координата установлена с такой же точностью.
Решение. Запишем соотношение неопределенностей для импульса и координаты
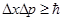 . (1)
. (1)
Так как импульс представляет собой произведение массы на скорость, то запишем это же соотношение для двух случаев – для электрона и для пылинки. Найдем минимальное значение неопределенности скорости электрона, для чего в выражении (1) положим равенство левой и правой частей.
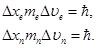
Выразим скорости электрона и пылинки и найдем их отношение
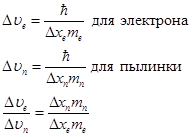
Согласно условию задачи, неопределенность координаты электрона такая же, как и неопределенность координаты пылинки, поэтому их можно
сократить
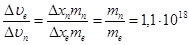 .
.
Задача 14.На грань кристалла никеля падает параллельный пучок электронов. Кристалл поворачивают так, что угол скольжения θ изменяется. Когда этот угол делается равным 64°, наблюдается максимальное отражение электронов, соответствующее дифракционному максимуму первого порядка. Принимая расстояние d между атомными плоскостями кристалла равным 200 пм, определить длину волны де Бройля λ электронов и их скорость υ.
Решение. К расчету дифракции электронов от кристаллической решетки применятся то же уравнение Вульфа-Брэгга, которое используется в случае рентгеновского излучения
2 d sin θ = k λ ,
где d – расстояние между атомными плоскостями кристалла; θ – угол скольжения, k – порядковый номер дифракционного максимума, λ – длина волны де Бройля.
Очевидно, что
λ = 2 d sin θ / k .
Подставив в эту формулу значения величин, получим значение длины волны λ = 360 пм.
Из формулы длины волны де Бройля
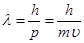 ,
,
выразим скорость движения электрона
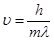 .
.
Подставив в эту формулу значения h, me (масса электрона), λ и произведя вычисления, получим υ = 2 Мм/с.
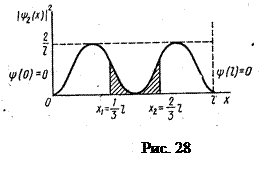 Задача 15.Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике шириной l. Вычислить вероятность того, что электрон, находящийся в возбужденном состоянии (n = 2), будет обнаружен в средней трети ящика (Рис. 28).
Задача 15.Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике шириной l. Вычислить вероятность того, что электрон, находящийся в возбужденном состоянии (n = 2), будет обнаружен в средней трети ящика (Рис. 28).
Решение. Вероятность W обнаружить частицу в интервале x1 < x < x2 определяется равенством
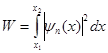 , (1) .
, (1) .
где ψn(x) – нормировочная собственная волновая функция, отвечающая данному состоянию частицы.
Нормировочная собственная волновая функция, описывающая состояние электрона в потенциальном ящике,
имеет вид
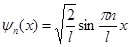 . (2)
. (2)
Возбужденному состоянию (n = 2) отвечает собственная функция
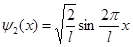 . (3)
. (3)
Подставив ψ2(x) из формулы (3) в подынтегральное выражение формулы (1), и вынося постоянные величины за знак интеграла, получим
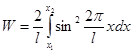 . (4)
. (4)
Согласноусловию задачи, х1 = ⅓ • l и х2 = ⅔ • l. Подставим эти пределы интегрирования в формулу (4) и произведем замену
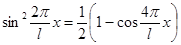
и разобьем интеграл на два интеграла
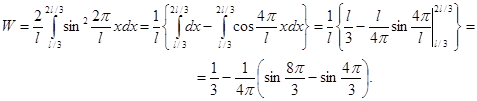
Заметив, что
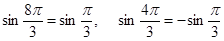
получим W = 0,195.
Задача 16.Моноэнергетический поток электронов (E = 100 эВ) падает на низкий прямоугольный потенциальный барьер бесконечной ширины. Определить высоту потенциального барьера U, если известно, что 4% падающих на барьер электронов отражается (Рис. 29).
Решение. Прямоугольный потенциальный барьер называют низким, если энергия Е частицы больше высоты U потенциального барьера. Коэффициент отражения ρ от низкого потенциального барьера выражается формулой
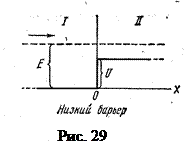
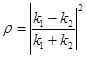 ,
,
где k1 и k2 – волновые числа, отвечающие движению электронов в областях, соответствующих координате x низкого потенциального барьера в области больше и меньше нуля соответственно.
В области, где координата х меньше нуля, значение высоты барьера U равно нулю, кинетическая энергия электрона будет равна E, и волновое число
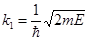 .
.
Поскольку координата электрона не определена, то импульс электрона определяется точно, и в данном случае можно говорить о точном значении кинетической энергии.
Во второй области с координатой х большей нуля, находиться потенциальный барьер с энергией U, и поэтому кинетическая энергия электрона будет равна E – U и волновое число
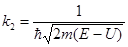 .
.
В случае низкого потенциального барьера коэффициент отражения может быть записан в виде
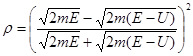 .
.
Разделим числитель и знаменатель дроби на 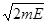
.
Решая уравнение относительно 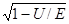 , получим
, получим
.
Возведя обе части равенства в квадрат, найдем высоту потенциального барьера 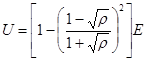 .
.
Подставив сюда значение величин, и произведя вычисления, найдем
U = 55,6 эВ.
Задача 17.Электрон с энергией E = 4,9 эВ движется в положительном направлении оси х. Высота U потенциального барьера равна 5 эВ. При какой ширине барьера d вероятность W прохождения электрона через него будет равна 0,2.
Решение. Вероятность прохождения частицы через потенциальный барьер по своему физическому смыслу совпадает с коэффициентом прозрачности D (W = D). Тогда вероятность того, что электрон пройдет через прямоугольный потенциальный барьер, выразится соотношением
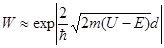 , (1)
, (1)
где m – масса электрона. Логарифмируя это выражение, получим
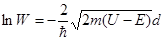 .
.
Для удобства вычислений изменим знак у правой и левой части этого равенства и найдем d
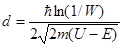 .
.
Входящие в эту формулу величины выразим в единицах СИ, произведем вычисления и получим d = 0,495 нм.
Учитывая, что формула приближенная, и вычисления носят оценочный характер, можно принять d = 0,5 нм.
ТАБЛИЦА ВАРИАНТОВ К КОНТРОЛЬНОЙ РАБОТЕ № 3
