Решение системы линейных уравнений методом Крамера
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля.
Пусть нам требуется решить систему линейных уравнений вида
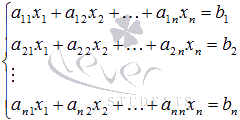
где x1, x2, …, xn – неизвестные переменные, ai j , i = 1, 2, …, n, j = 1, 2, …, n – числовые коэффициенты, b1, b2, …, bn - свободные члены. Решением СЛАУ называется такой набор значений x1, x2, …, xn при которых все уравнения системы обращаются в тождества.
В матричном виде эта система может быть записана как A ⋅ X = B, где 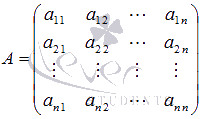
- основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных,
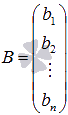
- матрица – столбец свободных членов, а
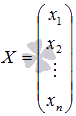
- матрица – столбец неизвестных переменных. После нахождения неизвестных переменных x1, x2, …, xn, матрица
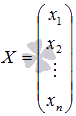
становится решением системы уравнений и равенство A ⋅ X = B обращается в тождество 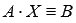 .
.
Будем считать, что матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера.
Метод Крамера основывается на двух свойствах определителя матрицы:
- Определитель квадратной матрицы

равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:
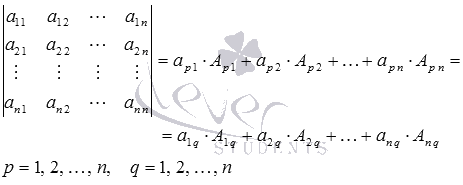
- Сумма произведений элементов какой-либо строки (столбца) квадратной матрицы на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю:
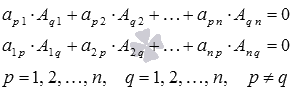
Итак, приступим к нахождению неизвестной переменной x1. Для этого умножим обе части первого уравнения системы на А1 1 , обе части второго уравнения – на А2 1 , и так далее, обе части n-ого уравнения – на Аn 1 (то есть, уравнения системы умножаем на соответствующие алгебраические дополнения первого столбца матрицы А):
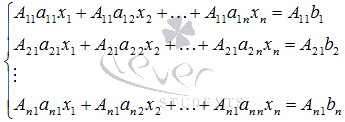
Сложим все левые части уравнения системы, сгруппировав слагаемые при неизвестных переменных x1, x2, …, xn, и приравняем эту сумму к сумме всех правых частей уравнений:
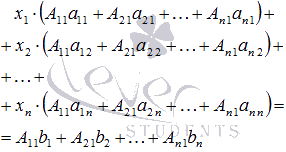
Если обратиться к озвученным ранее свойствам определителя, то имеем
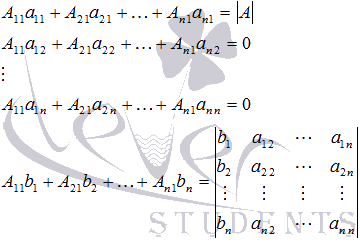
и предыдущее равенство примет вид
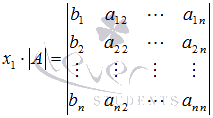
откуда
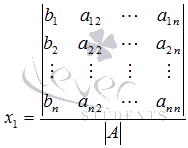
Аналогично находим x2. Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А:
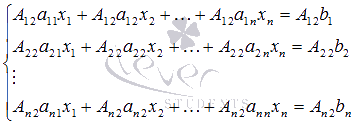
Складываем все уравнения системы, группируем слагаемые при неизвестных переменных x1, x2, …, xn и применяем свойства определителя:
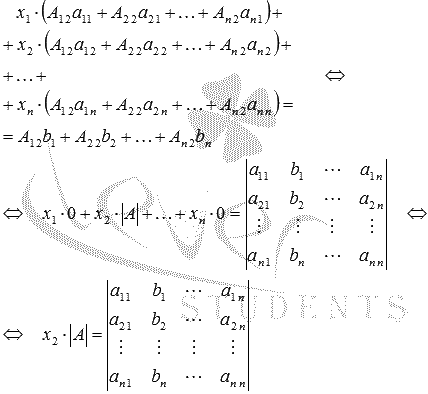
Откуда
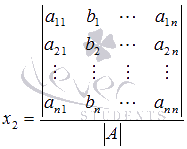 .
.
Аналогично находятся оставшиеся неизвестные переменные.
Если обозначить
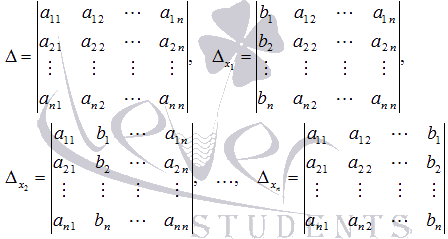
то получаем формулы для нахождения неизвестных переменных по методу Крамера 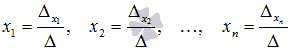 .
.
Пример.
Найдите решение неоднородной системы линейных алгебраических уравнений методом Крамера.
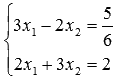
Решение.
Основная матрица системы имеет вид
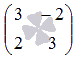 .
.
Вычислим ее определитель по формуле
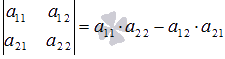 :
:
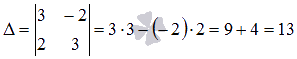
Так как определитель основной матрицы системы отличен от нуля, то СЛАУ имеет единственное решение, и оно может быть найдено методом Крамера. Запишем определители 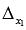 и
и 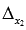 . Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель
. Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель
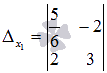 .
.
Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем
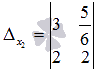 .
.
Вычисляем эти определители:
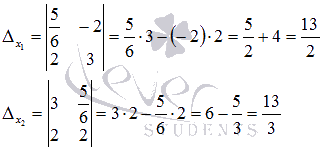
Находим неизвестные переменные x1 и x2 по формулам
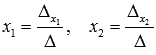 :
:
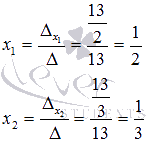
Выполним проверку. Подставим полученные значения x1 и x2 в исходную систему уравнений:
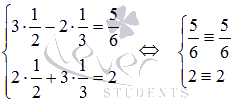
Оба уравнения системы обращаются в тождества, следовательно, решение найдено верно.
