Тема 13 Решение линейных неравенств с одной переменной
| Теория | Практика |
| Основная идея решения неравенства состоит в следующем: мы заменяем данное неравенство другим, но равносильным данному. Такие замены осуществляются на основе следующих утверждений: 1. Если какой-либо член неравенства с переменной перенести из одной части неравенства в другую с противоположным знаком, оставив при этом без изменения знак неравенства, то получится неравенство равносильное данному. 2. Если обе части неравенства с переменной умножить или разделить на одно и тоже положительное число, оставив при этом без изменения знак неравенства, то получится неравенство равносильное данному. Если обе части неравенства с переменной умножить или разделить на одно и тоже отрицательное число, заменив при этом знак неравенства на противоположный, то получится неравенство равносильное данному. | 1.Решить неравенство: 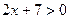 . Решение. Согласно утверждению 1, получим: . Решение. Согласно утверждению 1, получим: 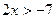 . По утверждению 2: . По утверждению 2: 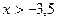 . Промежуток . Промежуток 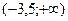 будет являться решением неравенства. Ответ: будет являться решением неравенства. Ответ: 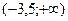 . 2. Решите неравенство: . 2. Решите неравенство: 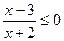 . Решение. 1) Решим неравенство методом интервалов. Найдем нули функций, стоящих в числителе и знаменателе: . Решение. 1) Решим неравенство методом интервалов. Найдем нули функций, стоящих в числителе и знаменателе: 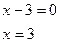 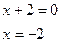 2) Отметим на числовой прямой точки: 2) Отметим на числовой прямой точки: 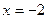 , , 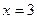 . Две точки разобьют прямую на 3 промежутка. . Две точки разобьют прямую на 3 промежутка.  Определим знак дроби на каждом промежутке и выберем те из них, где дробь отрицательна. Множество решений неравенства состоит из интервала и Определим знак дроби на каждом промежутке и выберем те из них, где дробь отрицательна. Множество решений неравенства состоит из интервала и 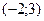 , в каждой точке которого функция отрицательна, а также значении , в каждой точке которого функция отрицательна, а также значении 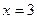 , при котором дробь равна нулю. Таким образом, решением неравенства является промежуток , при котором дробь равна нулю. Таким образом, решением неравенства является промежуток 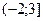 . Ответ: . Ответ: 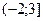 . . |
Реши сам:
1. Решите неравенство 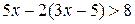
1) 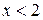 2)
2) 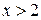 3)
3) 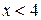 4)
4) 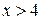
2. Решите неравенство 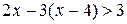
1) 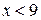 2)
2) 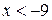 3)
3) 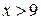 4)
4) 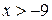
3. Решите неравенство 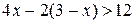
1) 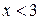 2)
2) 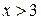 3)
3) 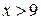 4)
4) 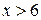
4. Решите неравенство 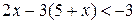
1) 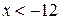 2)
2) 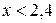 3)
3) 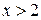 4)
4) 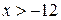
5. Решите неравенство 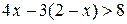
1) 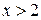 2)
2) 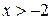 3)
3) 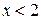 4)
4) 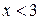
6. Решите неравенство 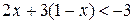
1) 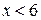 2)
2) 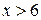 3)
3) 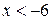 4)
4) 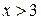
7. Решите неравенство 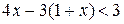
1) 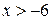 2)
2) 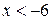 3)
3) 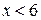 4)
4) 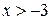
8. Решите неравенство 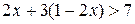
1) 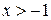 2)
2) 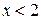 3)
3) 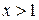 4)
4) 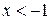
9. Решите неравенство 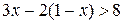
1) 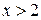 2)
2) 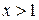 3)
3) 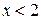 4)
4) 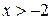
10. Решите неравенство 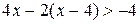
1) 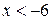 2)
2) 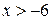 3)
3) 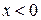 4)
4) 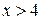
Вернуться в содержание
Тема 14 Решение квадратного неравенства с опорой на готовый график квадратичной функции
| Теория и практика | |
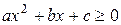 , , 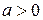 | 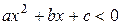 , , 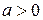 |
Если 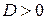 , то , то 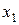 , , 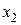 - корни - корни 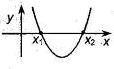 Ответ: Ответ: 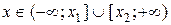 | Если 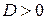 , то , то 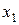 , , 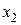 - корни - корни 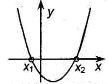 Ответ: Ответ: 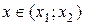 |
Если 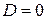 , то , то 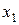 - корень - корень 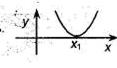 Ответ: Ответ: 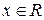 | Если 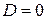 , то , то 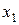 - корень - корень 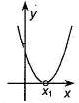 Ответ: Ответ: 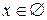 |
Если 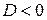 , то корней нет , то корней нет 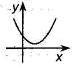 Ответ: Ответ: 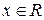 | 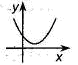 Если Если 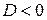 , то корней нет Ответ: , то корней нет Ответ: 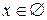 |
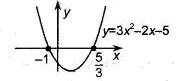 Пример: Пример: 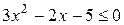 . Рассмотрим . Рассмотрим 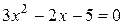 . . 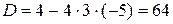 : : 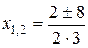 ; ; 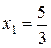 , , 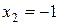 Ответ: Ответ: 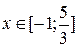 . . |
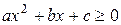 , , 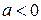 | 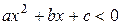 , , 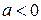 |
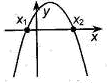 Если Если 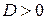 , то , то 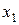 , , 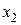 - корни Ответ: - корни Ответ: 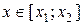 | Если 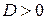 , то , то 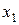 , , 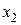 - корни - корни 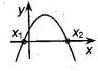 Ответ: Ответ: 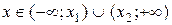 |
Если 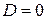 , то , то 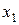 - корень - корень 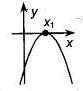 Ответ: Ответ: 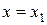 | Если 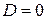 , то , то 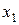 - корень - корень 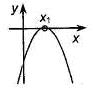 Ответ: Ответ: 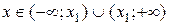 |
Если 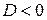 , то корней нет , то корней нет 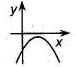 Ответ: Ответ: 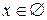 | Если 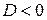 , то корней нет , то корней нет 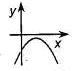 Ответ: Ответ: 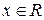 |
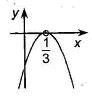 Пример: Пример: 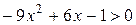 . Рассмотрим . Рассмотрим 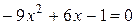 ; ; 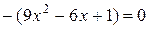 ; ; 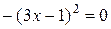 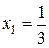 Ответ: Ответ: 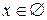 . . |
Реши сам
1. На рисунке изображен график функции 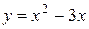 . Используя график, решите неравенство . Используя график, решите неравенство 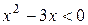 . 1) . 1) 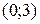 2) 2) 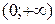 3) 3) 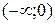 4) 4) 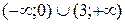 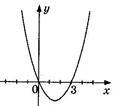 | 2. На рисунке изображен график функции 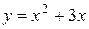 . Используя график, решите неравенство . Используя график, решите неравенство 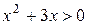 . 1) . 1) 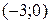 2) 2) 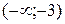 3) 3) 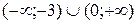 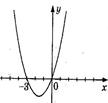 4) 4) 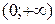 |
3. На рисунке изображен график функции 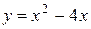 . Используя график, решите графически неравенство . Используя график, решите графически неравенство 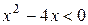 . . 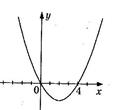 1) 1) 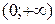 2) 2) 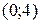 3) 3) 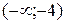 4) 4) 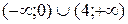 | 4. На рисунке изображен график функции 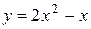 . Используя график, решите графически неравенство . Используя график, решите графически неравенство 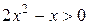 . . 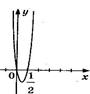 1) 1) 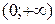 2) 2) 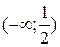 3) 3) 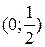 4) 4) 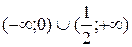 |
5. На рисунке изображен график функции 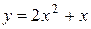 . Используя график, решите графически неравенство . Используя график, решите графически неравенство 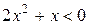 . . 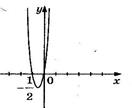 1) 1) 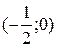 2) 2) 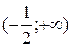 3) 3) 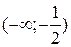 4) 4) 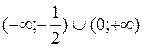 | 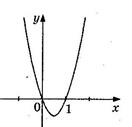 6. На рисунке изображен график функции 6. На рисунке изображен график функции 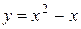 . Используя график, решите графически неравенство . Используя график, решите графически неравенство 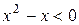 . 1) . 1) 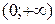 2) 2) 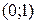 3) 3) 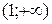 4) 4) 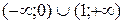 |
7. На рисунке изображен график функции 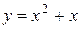 . Используя график, решите графически неравенство . Используя график, решите графически неравенство 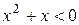 . . 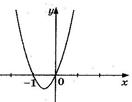 1) 1) 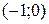 2) 2) 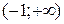 3) 3) 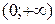 4) 4) 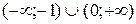 | 8. На рисунке изображен график функции 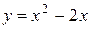 . Используя график, решите графически неравенство . Используя график, решите графически неравенство 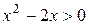 . 1) . 1) 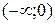 2) 2) 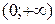 3) 3) 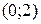 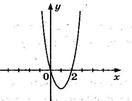 4) 4) 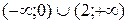 |
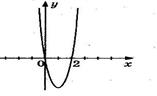 9. На рисунке изображен график функции 9. На рисунке изображен график функции 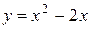 . Используя график, решите графически неравенство . Используя график, решите графически неравенство 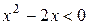 . 1) . 1) 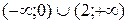 2) 2) 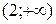 3) 3) 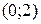 4) 4) 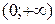 | 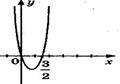 10. На рисунке изображен график функции 10. На рисунке изображен график функции 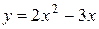 . Используя график, решите графически неравенство . Используя график, решите графически неравенство 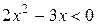 . 1) . 1) 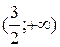 2) 2) 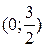 3) 3) 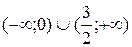 4) 4) 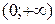 |
Вернуться в содержание
