Основные свойства определенного интеграла
1) 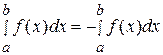 ; 2)
; 2) 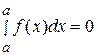 ;
;
3) 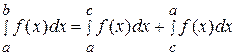 ;
;
4) 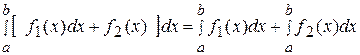 ;
;
5) 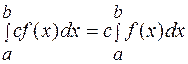 , где
, где 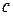 - постоянная.
- постоянная.
Правила вычисления определенного интеграла
1) Формула Ньютона-Лейбница:
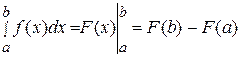 ,
,
где 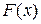 - первообразная для
- первообразная для 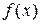 .
.
2) Интегрирование по частям:
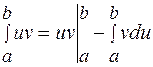 ,
,
где 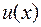 и
и 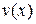 - непрерывные и дифференцируемые функции на отрезке
- непрерывные и дифференцируемые функции на отрезке 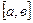 .
.
3) Замена переменной:
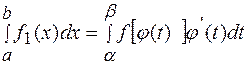 ,
,
где 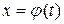 - функция, непрерывная вместе со своей производной
- функция, непрерывная вместе со своей производной 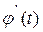 на отрезке
на отрезке 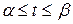 .
.
4) 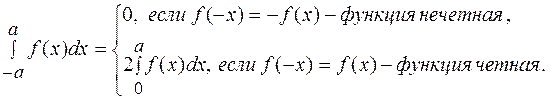
Пример 29 Вычислить:
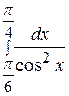 .
.
Решение.
По формуле Ньютона-Лейбница будем иметь:
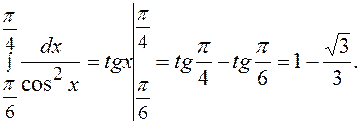
Пример 30. Вычислить:
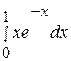 .
.
Решение.
Используем формулу интегрирования по частям:
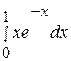 =
= 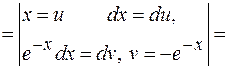
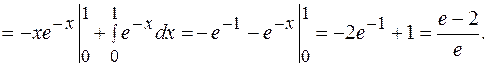
Пример 31 Вычислить:
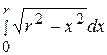 .
.
Решение.
Сделаем замену переменной: 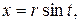
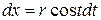 ;
; 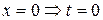 ;
; 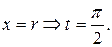
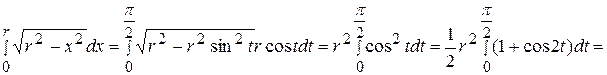
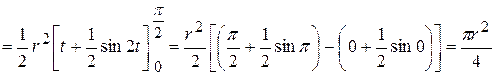 .
.
Приложения определенного интеграла
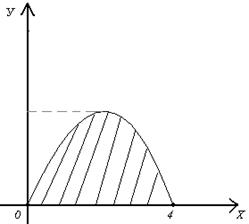
Вычисление площадей плоских фигур
Используя геометрический смысл определенного интеграла, нетрудно получить формулу для вычисления площади плоской фигуры, ограниченной кривыми 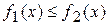 и прямыми
и прямыми 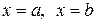 :
:
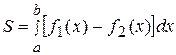 .
.
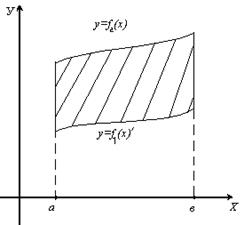
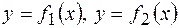
Пример 32
Вычислить площадь фигуры, ограниченной параболой 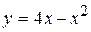 и осью
и осью 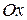 .
.
Решение.
Парабола пересекает ось 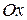 в точках
в точках 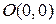 и
и 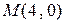
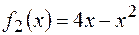 ,
,
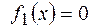 .Поэтому:
.Поэтому: 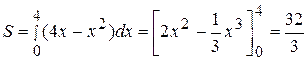 (кв.ед.).
(кв.ед.).
Вычисление объемов тел вращения
При вращении криволинейной трапеции, ограниченной линиями: 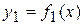 ,
, 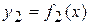 ,
, 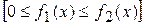
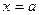 ;
; 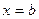 вокруг оси
вокруг оси 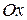 , получим объем тела вращения:
, получим объем тела вращения:
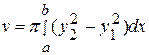 .
.
Пример 33
Найти объем тела, образованного вращением вокруг оси 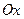 фигуры, ограниченной кривой
фигуры, ограниченной кривой 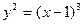 и прямой
и прямой 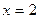 .
.
Решение.
Для построения кривой найдем точки:
при 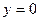 ,
, 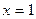 ; при
; при 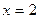 ,
, 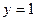 .
.
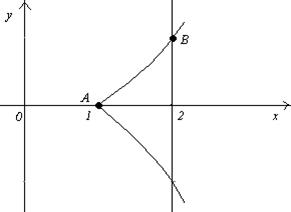
А(1,0); В(2,1)

Вычисление длины дуги плоской кривой
Если кривая 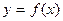 имеет непрерывную производную на отрезке
имеет непрерывную производную на отрезке 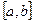 , то длина дуги этой кривой находится по формуле:
, то длина дуги этой кривой находится по формуле:
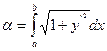 .
.
Пример 34
Найти длину дуги кривой 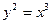 от
от 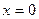 до
до 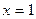 (
( 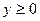 ).
).
Решение.
Найдем 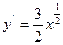 . Тогда
. Тогда 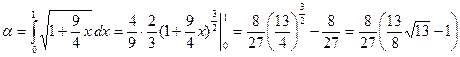 .
.
Вопросы для самопроверки
1. Что называется интегральной суммой для функции 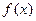 на отрезке
на отрезке 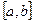 ?
?
2. Что называется определенным интегралом?
3. Каковы геометрический и физический смыслы определенного интеграла?
4. Назовите основные свойства определенного интеграла.
5. Назовите основные методы (правила) вычисления определенного интеграла.
6. Перечислите основные приложения определенного интеграла.
Индивидуальные задания для контрольной работы №2
Задача №1
Найти производные функций
1. а) 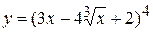 , б)
, б) 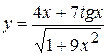 ,
,
в) 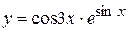 , г)
, г) 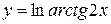 ,
,
д) 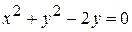 .
.
2. а) 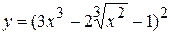 , б)
, б) 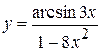 ,
,
в) 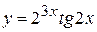 , г)
, г) 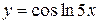 ,
,
д) 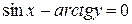 .
.
3. а) 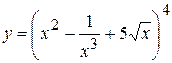 , б)
, б) 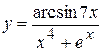 ,
,
в) 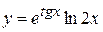 , г)
, г) 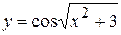 .
.
д) 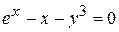 .
.
4. а) 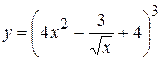 , б)
, б) 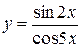 ,
,
в) 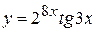 , г)
, г) 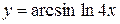 ,
,
д) 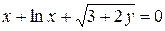 .
.
5. а) 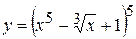 , б)
, б) 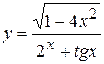 ,
,
в) 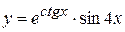 , г)
, г) 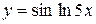 ,
,
д) 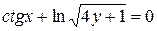 .
.
6. а) 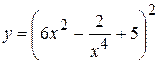 , б)
, б) 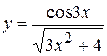 ,
,
в) 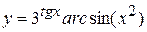 , г)
, г) 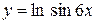 ,
,
д) 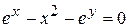 .
.
7. а) 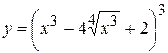 , б)
, б) 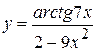 ,
,
в) 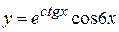 , г)
, г) 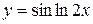 ,
,
д) 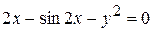 .
.
8. а) 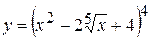 , б)
, б) 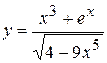 ,
,
в) 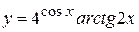 , г)
, г) 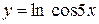 ,
,
д) 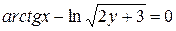 .
.
9. а) 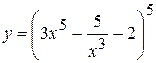 , б)
, б) 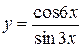 ,
,
в) 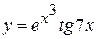 , г)
, г) 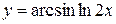 ,
,
д) 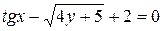 .
.
10. а) 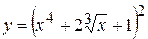 , б)
, б) 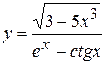 ,
,
в) 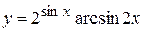 , г)
, г) 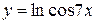 ,
,
д) 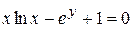 .
.
11. а) 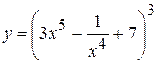 , б)
, б) 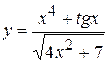 ,
,
в) 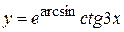 , г)
, г) 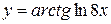 ,
,
д) 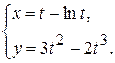
12. а) 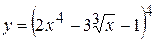 , б)
, б) 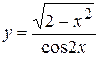 ,
,
в) 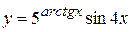 , г)
, г) 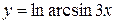 ,
,
д) 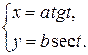
13. а) 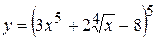 , б)
, б) 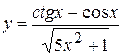 ,
,
в) 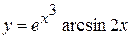 , г)
, г) 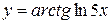 ,
,
д) 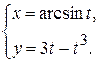
14. а) 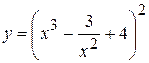 , б)
, б) 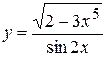 ,
,
в) 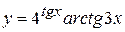 , г)
, г) 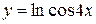 ,
,
д) 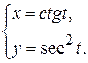
15. а) 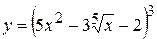 , б)
, б) 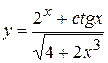 ,
,
в) 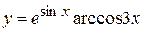 , г)
, г) 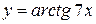 ,
,
д) 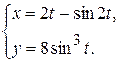
16. а) 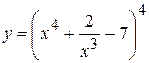 , б)
, б) 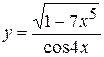 ,
,
в) 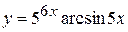 , г)
, г) 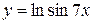 ,
,
д) 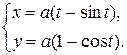
17. а) 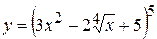 , б)
, б) 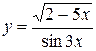 ,
,
в) 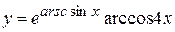 , г)
, г) 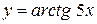 ,
,
д) 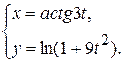
18. а) 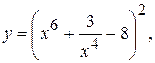 б)
б) 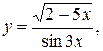
в) 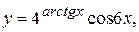 г)
г) 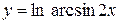 ,
,
д) 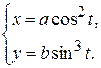
19. а) 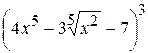 , б)
, б) 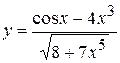 ,
,
в) 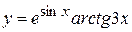 , г)
, г) 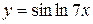 ,
,
д) 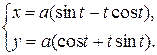
20. а) 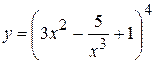 , б)
, б) 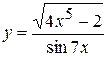 ,
,
в) 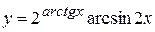 , г)
, г) 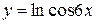 ,
,
д) 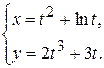
Задача №2
Исследовать функцию методами дифференциального исчисления и построить ее графики:
1. 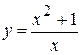 . 7.
. 7. 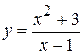 . 14.
. 14. 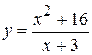 .
.
2. 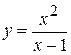 . 8.
. 8. 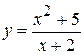 . 15.
. 15. 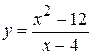 .
.
3. 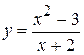 . 9.
. 9. 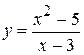 . 16.
. 16. 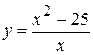 .
.
4. 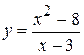 . 10.
. 10. 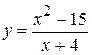 . 17.
. 17. 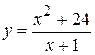 .
.
5. 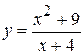 . 11.
. 11. 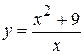 . 18.
. 18. 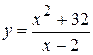 .
.
6. 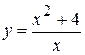 . 12.
. 12. 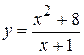 . 19.
. 19. 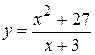 .
.
13. 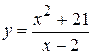 . 20.
. 20. 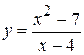 .
.
Задача №3
Найти неопределенные интегралы способом подстановки (методом замены переменного).
1. 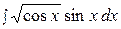 7.
7. 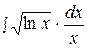 14.
14. 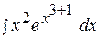
2. 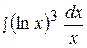 8.
8. 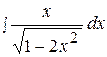 15.
15. 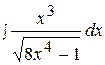
3. 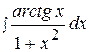 9.
9. 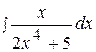 16.
16. 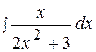
4. 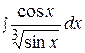 10.
10. 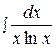 17.
17. 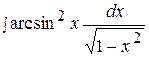
5. 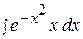 11.
11. 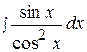 18.
18. 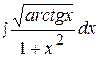
6. 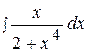 12.
12. 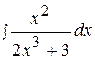 19.
19. 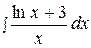
13. 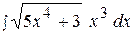 20.
20. 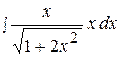
Задача №4
Найти неопределенные интегралы, используя выделение полного квадрата.
1. 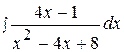
 11.
11. 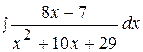
2. 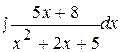 12.
12. 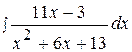
3. 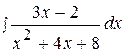 13.
13. 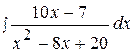
4. 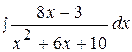 14.
14. 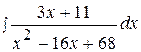
5. 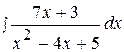 15.
15. 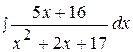
6. 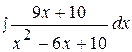 16.
16. 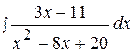
7. 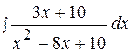 17.
17. 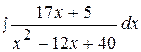
8. 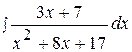 18.
18. 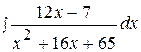
9. 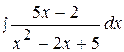 19.
19. 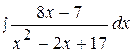
10. 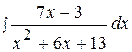 20.
20. 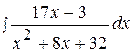
Задача №5
Найти неопределенные интегралы, применяя метод интегрирования по частям.
1. 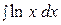
 11.
11. 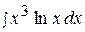
2. 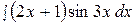 12.
12. 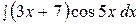
3. 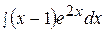 13.
13. 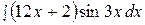
4. 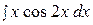 14.
14. 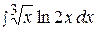
5. 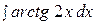 15.
15. 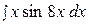
6. 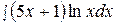 16.
16. 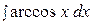
7. 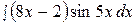 17.
17. 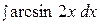
8. 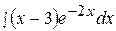 18.
18. 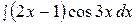
9. 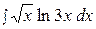 19.
19. 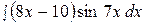
10. 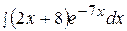 20.
20. 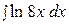
Задача №6
Найти неопределенные интегралы, пользуясь разложением рациональных дробей на простейшие.
1. 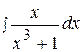
 11.
11. 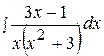
2. 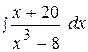 12.
12. 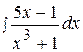
3. 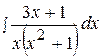 13.
13. 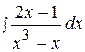
4. 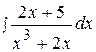 14.
14. 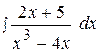
5. 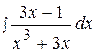 15.
15. 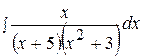
6. 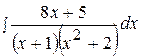 16.
16. 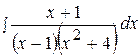
7. 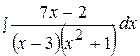 17.
17. 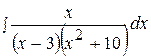
8. 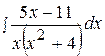 18.
18. 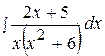
9. 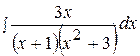 19.
19. 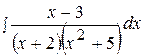
10. 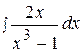 20.
20. 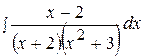
Задача №7
Вычислить площадь, ограниченную заданными параболами.
1. y= 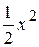 -x+1; 7. у=2
-x+1; 7. у=2  -6х+1;
-6х+1;
у= - 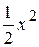 +3x+6. у= -
+3x+6. у= -  +х-1.
+х-1.
2. y= 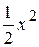 +x+2; 8. у=
+x+2; 8. у= 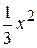 -2х+4;
-2х+4;
y= - 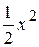 -5x+7. у= -
-5x+7. у= - 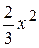 -х+2.
-х+2.
3. y= 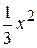 -3x+2; 9. у=
-3x+2; 9. у=  -5х-3;
-5х-3;
y= - 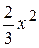 -2x+4. у= - 3
-2x+4. у= - 3  +2х-1.
+2х-1.
4. y=2  +6х-3; 10. у=
+6х-3; 10. у=  -2х-5;
-2х-5;
y= -  +х+5. у= -
+х+5. у= -  -х+1.
-х+1.
5. y=3  -5х-1; 11. у=
-5х-1; 11. у= 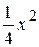 -2х-5;
-2х-5;
y= -  +2х+1. у= -
+2х+1. у= - 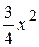 -х+1.
-х+1.
6. у=  -3х-1; 12. у=
-3х-1; 12. у= 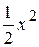 +3х-2;
+3х-2;
у= -  -2х+5. у= -
-2х+5. у= - 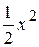 -х+3.
-х+3.
Задача №8
Найти объем тела, образованного вращением вокруг оси Ох фигуры, расположенной в первом квадранте и ограниченной заданными параболой, прямой и осью Ох.
1. y= 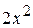 ; 11. у=2
; 11. у=2  ;
;
у= - 2х +4. у= - 3х +14.
2. y=  ; 12. у=
; 12. у= 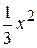 ;
;
y = - x+2. у= - х +6.
3. y = 3  ; 13. у =3
; 13. у =3  ;
;
y = - x+4. у =- 2х+5.
4. y = 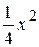 ; 14. у =
; 14. у = 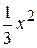 ;
;
y = - х+3. у = - 2х+9.
5. y = 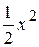 ; 15. у =
; 15. у = 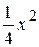 ;
;
y = -3х +8. у = - 2х+6.
6. у = 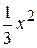 ; 16. у = 2
; 16. у = 2  ;
;
у= - 3х +12. у = - х+10.
7. у = 4  ; 17. у =3
; 17. у =3  ;
;
у = - 2х +2. у =- 3х+6.
8. у = 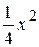 ; 18. у=
; 18. у=  ;
;
у = - 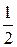 х+2. у =-2х +5
х+2. у =-2х +5
9. у =4  ; 19. у =
; 19. у = 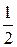
 ;
;
у= - 2х +6. у = - х +3.
10. у=  ; 20. у =3
; 20. у =3  ;
;
у= - х+3. у = -5х +8.
Задача №9
Найти длину дуги кривой.
1. y = 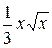 , 11.
, 11. 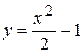 , отсеченной
, отсеченной
 . осью Ох.
. осью Ох.
2. y =ln sin x, 12. 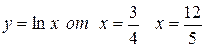
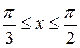 . 13.
. 13. 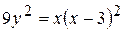 между
между
3. y = 1-ln cos x, точками пересечения с осями
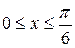 . Оу и Ох.
. Оу и Ох.
4. у = ln x, 14. 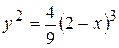 , отсеченной
, отсеченной
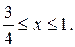 прямой х= -1.
прямой х= -1.
5. у =ln cos x, 15. у =ln(sin x) ,
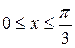
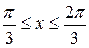 .
.
6. у = 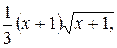 16. y= ln(1-
16. y= ln(1-  ),
),
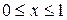
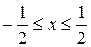 .
.
7. 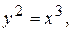 отсеченной 17.
отсеченной 17. 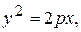 отсеченной
отсеченной
прямой 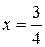 . прямой
. прямой 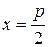 .
.
8. 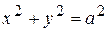 18. у =ln x,
18. у =ln x,
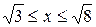 .
.
9. 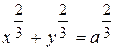 19. y = ln (1-
19. y = ln (1-  ),
),
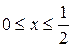 .
.
10. 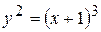 , отсеченной 20.
, отсеченной 20. 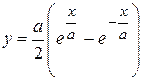 ,
,
прямой х=4 . 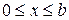
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Письменный Д. Т.
Конспект лекций по высшей математике : полный курс / Д. Т. Письменный . - 9-е изд. - М.: Айрис-Пресс, 2008. – 280с.- Ч. 1.
2. Пискунов Н. С.
Дифференциальное и интегральное исчисления: учеб. пособие для вузов / Н. С. Пискунов. - изд. стер.. - М.: Интеграл-Пресс, 2006. – 415 с. Т.1.
3. Шипачев В.С.
Курс высшей математики: учебник для вузов / В.С.Шипачев; Под редакцией А.Н. Тихонова. – 3-е изд., испр. – М.: Издательство Оникс, 2007 – 600с.: ил.
4. Берман Г. Н.
Сборник задач по курсу математического анализа: учеб. пособие / Г. Н. Берман. - 22-е изд., перераб. - СПб.: Профессия, 2006 - 432 с.
5. Лунгу К.Н.
Сборник задач по высшей математике: учеб. пособие / К.Н.Лунгу и др.- 7-е изд..- М.: Айрис Пресс, 2008.- 574 с.
6. Шипачев В. С.
Задачник по высшей математике: учеб. пособие для вузов / В. С. Шипачев. - 8-е изд., стер. - М.: Высш. шк., 2008. - 304 с.: ил.
7. Данко П. Е.
Высшая математика в упражнениях и задачах: учеб. пособие / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова . - 6-е изд.. - М.: ОНИКС.- 2008 .-368 с.- Ч.1.
