Некоторые способы задания плоской кривой

Введение

В курсе математического анализа разработана универсальная схема исследования функций вида y=f(x) и построения графиков этих функций. В школьном курсе математики выделены некоторые элементы этой теории. А вопросы, связанные с исследованием функций, заданных неявно, в школьном курсе не рассматриваются, да и в Вузовском курсе, по понятным причинам, не уделяется должного внимания. И в курсе «дифференциальной геометрии» исследованию плоских линий, в настоящие время, уделяется недостаточное внимание.

Тема данной работы «Исследование линий на плоскости. Приложения к школьному курсу математики». Тема достаточно актуальна в геометрии и в других разделах математики в том числе в школьном курсе. Это объясняется тем, что как в Вузовских, так и в школьных программах на эту тему выделяется малое количество академических часов.

Целью данной работы и является, рассмотрение основных вопросов данной теории и приложения данной теории к школьному курсу математики. При этом мы будем рассматривать только плоские кривые.

Исходя из данной цели, были поставлены следующие задачи:

- изучить основную литературу по данной теме;

- рассмотреть основные вопросы теории (понятие линии, исследование линий на плоскости);

- рассмотреть отдельные вопросы методики изучения линий на плоскости в школьном курсе математики;

- применить данную теорию к разработке соответствующего спецкурса для средней школы геометрии;

- разработать урок по данной теме.

Структура выпускной квалификационной работы: работа состоит из введения, двух глав, заключения, библиографического списка и приложения.

В первой главе рассмотрены основные понятия теории кривых, а также способы задания кривой.

Во второй главе рассмотрены некоторые вопросы методики изучения кривых на плоскости в школьном курсе математики.

В заключении рассмотрены отдельные вопросы, которые требуют дальнейших разработок.

В приложении приведен примерный план спецкурса и один из уроков по данной теме.

Глава I. Основные понятия теории кривых

Понятие кривой

Если для любого 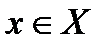по определенному правилу (закону) поставлен в соответствии единственный элемент 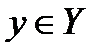, то говорят, что задано отображение (или функция).

Отображение топологического пространства 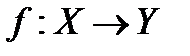называется гомеоморфизмом (или топологическим отображением), если:

1. f – биекция

2. f и f^-1 – непрерывны.

Далее мы рассматриваем множество 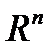с естественной топологией. Открытыми множествами U называем открытые шары (на 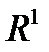U – интервал, на 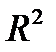U – открытый круг, на 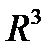U – открытый шар).

Окрестностью точки 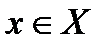называем любое открытое множество. 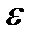- окрестностью точки 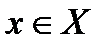( 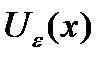) называют открытый шар с центром в точке x и радиусом ( ).

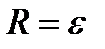Понятие отображения фигуры (множества точек) известно из элементарной геометрии. Если каждую точку фигуры F сместить каким-нибудь образом, то мы получим новую фигуру F'. Говорят, что она получена преобразованием из фигуры F. Преобразование фигуры F переводит близкие точки фигуры F в близкие точки фигуры F' . Это значит, что если точка X фигуры F переходит в точку X'  фигуры F' , то каково бы ни было  ε > 0, существует δ > 0 такое, что любая точка Y фигуры F, которая отстоит от X на расстоянии меньшем δ, переходит в точку фигуры F', которая отстоит от X' на расстоянии меньшем ε. Преобразование, переводящее различные точки фигуры F в различные точки фигуры F', называется топологическим, если это преобразование и обратное к нему преобразование фигуры F' в F непрерывны. Преобразование фигуры называется локально топологическим, если оно является топологическим в достаточно малой окрестности каждой ее точки.

Рисунок 2

Рисунок 1

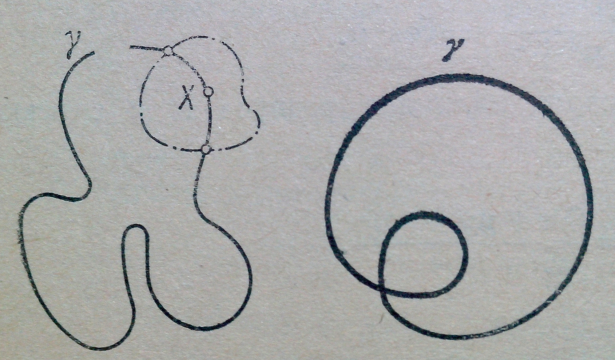Дадим теперь несколько определений, относящихся к понятию кривой. Элементарной кривой мы будем называть фигуру, полученную топологическим отображением открытого отрезка. Простой кривой будем называть фигуру, каждая точка которой имеет пространственную окрестность такую, что часть фигуры, содержащаяся в этой окрестности, является элементарной кривой (рис. 1). Общей кривой мы будем называть фигуру, полученную локально топологическим отображением простой кривой. Общая кривая на рисунке 2 получается локально топологическим преобразованием окружности.

Ввиду таких определений, изучение любой кривой «в малом» сводится к изучению элементарной кривой. Пусть γ - элементар­ная кривая, являющаяся топологическим преобразованием отрезка AB. Если на прямой AB как на числовой оси ввести координату t, то преобразование отрезка AB в кривуюγ можно задать уравнениями

(*)

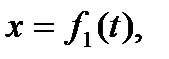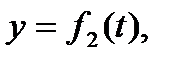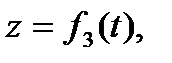где 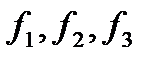- непрерывные функции, причем для различных значений t' и t"

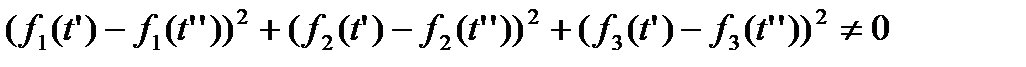
Уравнения (*) мы будем называть уравнениями кривой γ в па­раметрической форме (t — параметр). Элементарная кривая допу­скает различные задания в параметрической форме. Например, кривую γ можно задать уравнениями:

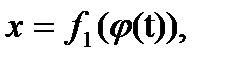
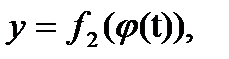
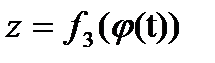
где 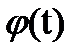— любая непрерывная строго монотонная функция от .

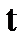Кривую γ мы будем называть регулярной (k раз дифференцируемой), если она допускает регулярную параметризацию, т. е. задание уравнениями в параметрической форме

,

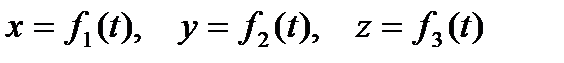где 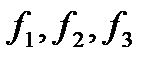- регулярные (k раз дифференцируемые) функции, удовлетворяющие условию

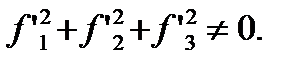
При k=1 кривая называется гладкой.

Кривая называется аналитической, если она допускает аналитическую параметризацию (функции 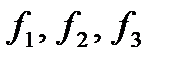— аналитические).

Некоторые кривые при подходящем выборе осей координат допускают параметрическое задание вида

,

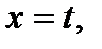
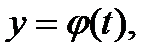
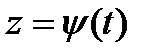или, что то же,

.

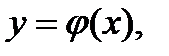
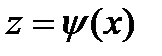Эта параметризация иногда оказывается очень удобной для исследования кривой. В связи с этим возникает вопрос: когда кривая хотя бы «в малом» допускает такую параметризацию? Ответ на этот вопрос дает следующее предложение:

Теорема 1.Пусть γ - регулярная кривая,

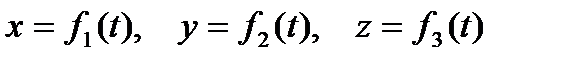
- ее регулярное параметрическое задание в окрестности точки 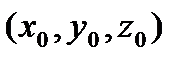, соответствующей 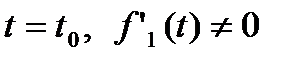, то в достаточно малой окрестности точки 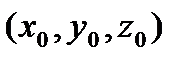кривая может быть задана уравнениями

где 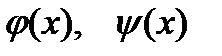- регулярные функции от x.

Некоторые способы задания плоской кривой

Кривая γ на плоскости σ задана явно, если в некоторой прямоугольной системе координат Oxy (ПДСК) одна из текущих координат её точки представляется в виде однозначной явной функции от другой координаты, т.е. имеет аналитическое представление в виде непрерывных функций, имеющих непрерывные производные к-го порядка:

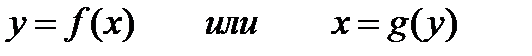(1)

Кривая γ на плоскости σ задана неявно, если в некоторой ПДСК кривая представлена уравнением вида

,

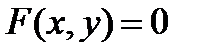(2)

неразрешимым ни относительно х, ни относительно у, при этом уравнение (2) называется неявным уравнением кривой.

Теорема. Пусть функция F(x,y) определена и непрерывна в некоторой окрестности точки 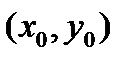, обращается в нуль в точке 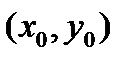, т.е. 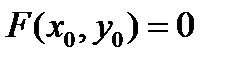, и при постоянной x функция 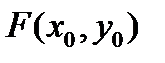монотонно возрастает (или монотонно убывает) с возрастанием у. Тогда:

1. В некоторой окрестности точки 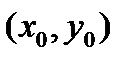уравнение (2) определяет у как однозначную функцию от х ( );

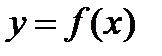2. При 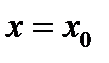эта функция принимает значение ( );

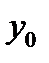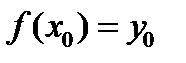3. Функция 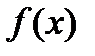непрерывна.

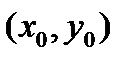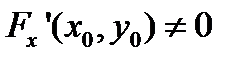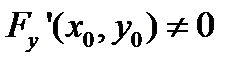Следствие 1. Если в точке кривой (2) выполнено условие или , то существует окрестность этой точки, в которой кривая γ может быть представлена явным уравнением (1) того или другого вида, при этом функции f или g и их производные 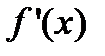или 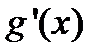непрерывны.

Следствие 2. Точки 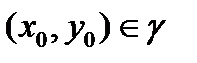, для которых выполняются сразу оба условия

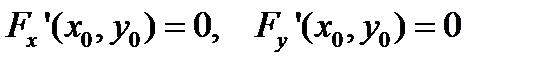(3)

имеют ту особенность, что в их окрестности кривая γ не может быть представлена явным уравнением 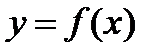ни , ни .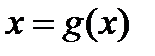

Точки кривой γ, удовлетворяющие уравнению (3), называют особыми, а остальные точки кривой называют обыкновенными.

Если зависимость у от х не задана уравнениями (1) или (2) (т.е. задана непосредственно), а задана зависимость обеих переменных х и у от некоторой третьей, вспомогательной, переменной (называемой параметром):

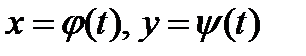(4)

то предполагая, что эти функции имеют производные 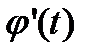и 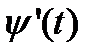, и для функции 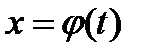существует обратная функция 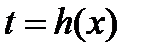, имеющая производную, то тогда у является функцией от х:

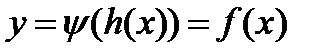(5)

для которой также существует производная .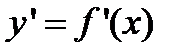

Если при этом рассматривать х и у как ПДСК на плоскости σ, то уравнение (4) каждому значению параметра t ставят в соответствие некоторую точку, которая с изменением t описывает кривую .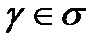

Уравнения (4) называют параметрическими уравнениями кривой γ на плоскости σ.

Рассмотрим точку 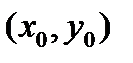кривой γ, заданной параметрическими уравнениями (4). Тогда данная точка определяется значением 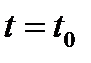параметра. Пусть при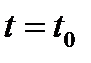 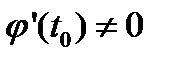. Тогда в окрестности t₀ производная 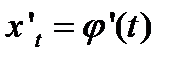- по непрерывности будет сохранять тот же знак, т.е. функция 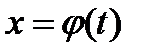будет монотонной в указанной окрестности точки t₀. При этих условиях можно t рассматривать как однозначную функцию от х: 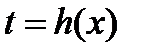, непрерывную и имеющую непрерывную производную 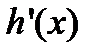. Подставляя эту функцию вместо t в выражение для y, получим зависимость y от x:

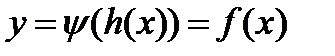
где, как и в случае неявного задания, функция f непрерывна вместе с производной 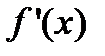и мы в определенной окрестности точки 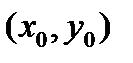плоскости σ выразим явным уравнением некоторую часть кривой γ, примыкающей к взятой точке t₀ (точке ).

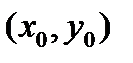Если предположить, чт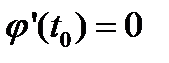о , но 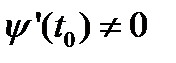,то также получим явное задание определенной выше части кривой γ, с той только разницей, что получится явное задание уравнения вида .

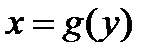Лишь в том случае, когда одновременно

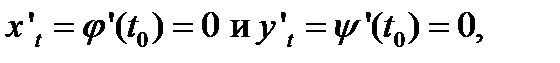(6)

кривая γ в окрестности рассматриваемой точки может оказаться не представимой явным уравнением.

Такую точку 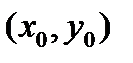кривой γ называют особой.

Может случиться так, что все выше сказанное об обыкновенной точке 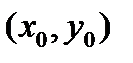, т.е. такой, для которой не выполняются условия (6), предполагает еще, что эта точка получается только при одном значении параметра t=t₀.

Такую обыкновенную точку 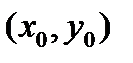кривой γ называют простой точкой.

Если точка 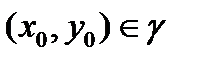является кратной, т.е. отвечает двум или нескольким параметрам t, то в ней, вообще говоря, пересекались бы два или более участков кривой γ, определяемые значениями t (t=t₁, t=t₂ и т.д.). В этом случае всю кривую в окрестности точки (x₀, y₀) опять – таки нельзя было бы представить явным уравнением.

Кратные точки кривой γ также называют особыми.

Замечание. Для замкнутой кривой заданной параметрически, точку 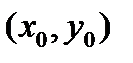- точку замыкания, которая отвечает двум кратным значениям параметра t, не считают кратной (особой).

Пример окружности:

.

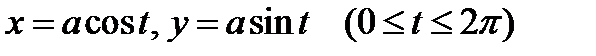Точку 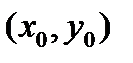окружности, отвечающую значениям параметра 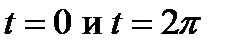, мы не считаем кратной.

Замечание. Геометрически образы, определяемые уравнениями (1), (2) и (4), в целом могут значительно разниться по своему виду, но в малом, в окрестности обыкновенной (а в случае параметрического задания (4) и простой) точки, все они могут быть заданы уравнением вида (1).