А.Г. Мордкович и др. «Алгебра и начала математического анализа» 10-11 класс

В учебнике Мордкович и др. для 10-11 классов базового уровня [6] тема посторонние графиков функций описывается в 5 главе «Производная». Перед самой темой «построение графиков функций» идет объяснение таких тем, как: предел последовательности, сумма бесконечной геометрической прогрессии, предел функции, определение производной, вычисление производных, уравнение касательной к графику функции, применение производной для исследования функций на монотонность и экстремумы. После этого списка идет тема «построение графиков функций» и завершающий параграф в главе «применение производной для нахождения наибольшего и наименьшего значения функции».

Каждый параграф, по идеи авторского состава, является академическим часом. Но большие для восприятия учениками параграфы разделены на подпункты, которые так же должны быть пройдены классом за академический час.

Почти все параграфы в данной главе построены по схеме:

1. Рассматривается частный случай

2. Вводятся определения, теоремы, частные случаи и т.д.

3. Рассматриваются несколько примеров, причем иногда пример может быть рассмотрен из темы, которая находится впереди учебного плана, но в этой же главе. Благодаря чему происходит актуализация знаний учащихся.

4. И в конце параграфа авторы учебника дают для учащихся алгоритм для исследования функции на критерий, описанный в параграфе. Т.о. они одновременно и подводят итог темы, и выделяют коротко необходимый материал для завершающего параграфа.

Сам параграф «построение графиков функций» начинается с того, что Мордкович напоминает читателям, что раннее ученики строили графики функции «по точкам», т.е. для заданной функции находили контрольные точки. Автор пишет, что данный метод хорош в тех ситуациях, когда есть представление или некоторый эскиз графика функции, но бывают ситуации, когда нет эскиза графика функции. После перечисляет «важные точки графика функции». А именно стационарные и критические точки, точки экстремума, точки пересечения графика с осями координат, точки разрыва функции.

В качестве конкретного алгоритма исследования функции для построения графика, редакция предлагает использовать их облегченный способ. Данный алгоритм состоит из 5 пунктов.

1. Если функция непрерывна на всей числовой прямой, то достаточно найти стационарные и критические точки, точки экстремума, определить монотонность, точки пересечения графика с осями координат

2. Если функция определена не на всей числовой прямой, то исследование стоит начитать с области определения функции и указания точек разрыва

3. Исследовать на четность/нечетность

4. Определить есть ли горизонтальная асимптота графика функции. Определять надо с помощью предела: 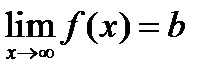, где 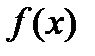- искомая функция, а асимптота совпадет с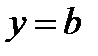

5. Определить есть ли вертикальная асимптота графика функции. Если 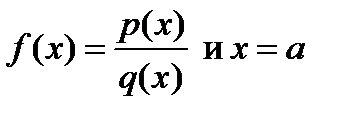знаменатель обращается в нуль, а числитель отличен от нуля, тогда 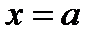является вертикальной асимптотой графика функции f(x)

Таким образом, Мордкович и др. представил отличный учебник для учеников 10-11 классов, благодаря которому дети могут получить необходимые знания из раздела предела, производной, а так же опираясь на данный материал построить график функции.