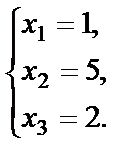Решение систем методом Гаусса
Одним из наиболее универсальных и эффективных методов решений систем линейных уравнений является метод Гаусса, состоящий в последовательном исключении неизвестных.
Пусть дана система уравнений
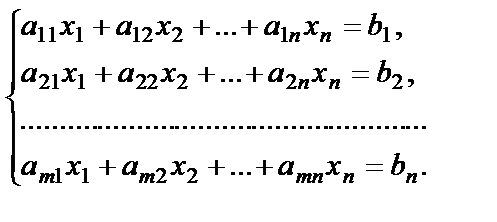 (25)
(25)
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (треугольному или трапециевидному) виду. Для этого над строками расширенной матрицы системы 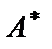 проводятся элементарные преобразования, приводящие эту матрицу к ступенчатому виду. Полученная матрица будет эквивалентной матрице
проводятся элементарные преобразования, приводящие эту матрицу к ступенчатому виду. Полученная матрица будет эквивалентной матрице  , значит и система уравнений, полученная с помощью новой матрицы будет равносильной данной системе уравнений.
, значит и система уравнений, полученная с помощью новой матрицы будет равносильной данной системе уравнений.
Если в процессе приведения системы (25) к ступенчатому виду появятся нулевые уравнения, то есть равенства вида 0=0, их отбрасывают. Если же появится уравнение вида 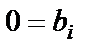 , а
, а 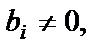 то это говорит о том, что данная система уравнений несовместна.
то это говорит о том, что данная система уравнений несовместна.
Второй этап (обратный ход) заключается в решении ступенчатой системы. Если в последнем уравнении новой системы содержится одно неизвестное, то исходная система имеет единственное решение. Из последнего уравнения находим 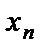 , из предпоследнего уравнения
, из предпоследнего уравнения 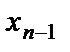 , далее поднимаясь по системе вверх, найдем все остальные неизвестные
, далее поднимаясь по системе вверх, найдем все остальные неизвестные 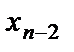 ,
,  . Если в последнем уравнении преобразованной системы более чем одно неизвестное, то данная система имеет множество решений (система является неопределенной). Из последнего уравнения выражаем первое неизвестное
. Если в последнем уравнении преобразованной системы более чем одно неизвестное, то данная система имеет множество решений (система является неопределенной). Из последнего уравнения выражаем первое неизвестное 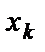 через остальные неизвестные
через остальные неизвестные 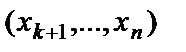 . Затем подставляем значение
. Затем подставляем значение 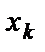 в предпоследнее уравнение системы и выражаем
в предпоследнее уравнение системы и выражаем 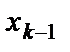 через
через 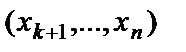 и так далее. Придавая свободным неизвестным
и так далее. Придавая свободным неизвестным 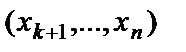 произвольные значения, получим бесчисленное множество решений системы. На практике удобно, чтобы коэффициент
произвольные значения, получим бесчисленное множество решений системы. На практике удобно, чтобы коэффициент 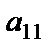 был равен 1 (уравнения переставить местами, либо разделить обе части первого уравнения на
был равен 1 (уравнения переставить местами, либо разделить обе части первого уравнения на 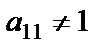 ).
).
Пример 37. Решить систему уравнений методом Гаусса:
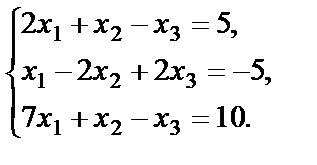
Решение. Составим расширенную матрицу  данной системы
данной системы
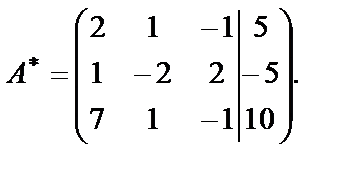
Так как 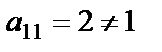 ,
, 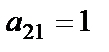 , поменяем местами первую и вторую строки матрицы
, поменяем местами первую и вторую строки матрицы  местами:
местами:
 ~
~ 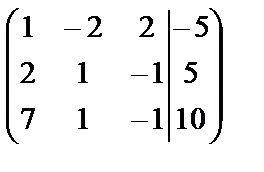 .
.
Сначала элементы первой строки умножим на (-2) и прибавим к соответствующим элементам второй строки, а затем элементы первой строки умножим на (-7) и прибавим к элементам третьей строки:
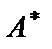 ~
~ 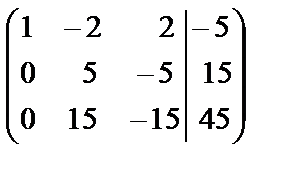 .
.
Элементы второй строки умножим на 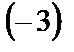 и прибавим к элементам третьей строки:
и прибавим к элементам третьей строки:
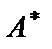 ~
~ 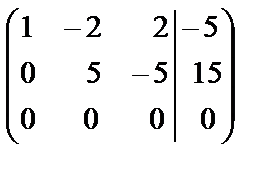 .
.
Восстановим систему по последней матрице
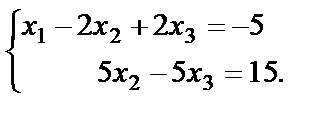
Получили систему, состоящую из двух уравнений и содержащую три неизвестных, то есть с помощью элементарных преобразований данную систему уравнений привели к ступенчатому виду, в которой нет уравнений вида 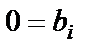 , где
, где 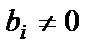 . Поэтому система уравнений имеет бесчисленное множество решений. Выразим
. Поэтому система уравнений имеет бесчисленное множество решений. Выразим 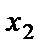 через
через 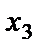 из второго уравнения:
из второго уравнения:
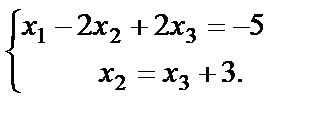
Подставим полученное выражение 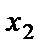 в первое уравнение:
в первое уравнение:
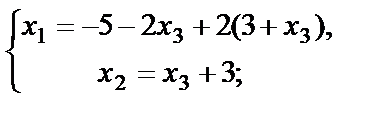
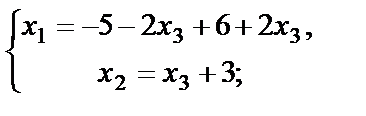
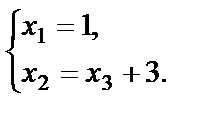
Пусть 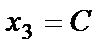 , где С – любое действительное число, тогда полученное решение будет называться общим решением
, где С – любое действительное число, тогда полученное решение будет называться общим решением
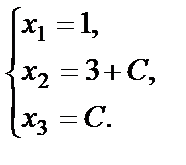
Пусть 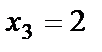 , тогда получаем решение, которое будет называться частным решением системы:
, тогда получаем решение, которое будет называться частным решением системы: 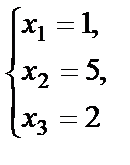
Пример 38. Решить систему уравнений методом Гаусса
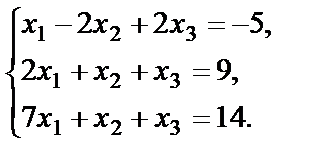
Решение. Составим расширенную матрицу 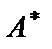 данной системы уравнений
данной системы уравнений
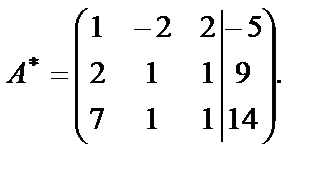
Элементы первой строки умножим на (-2) и прибавим к элементам второй строки, затем элементы первой строки умножим на (-7) и прибавим к элементам третьей строки:
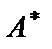 ~
~ 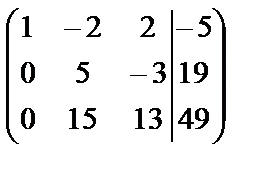 .
.
Элементы второй строки умножим на (-3) и прибавим к элементам третьей строки:
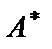 ~
~ 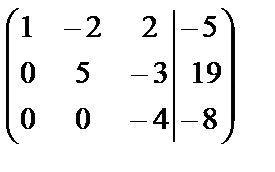 .
.
Элементы третьей строки умножим на 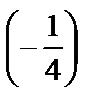 :
:
 ~
~ 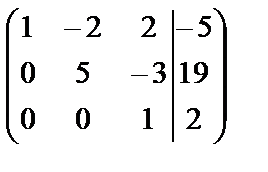 .
.
С помощью элементарных преобразований получили матрицу треугольного вида, значит, данная система уравнений имеет единственное решение.
С помощью полученной преобразованной расширенной матрицы запишем соответствующую систему уравнений
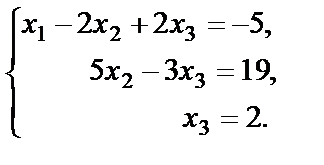
Зная значение 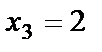 , из второго уравнения находим
, из второго уравнения находим 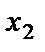 :
:
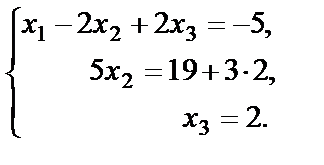 или
или 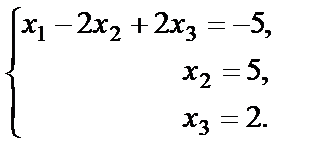
Используя значения 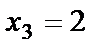 и
и 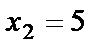 , из первого уравнения находим
, из первого уравнения находим 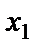 :
:
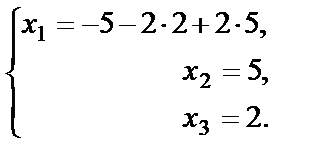 или окончательно
или окончательно