Лабораторная работа № 7
Пределы и непрерывность функций одной переменной
Теоретический минимум
1. Предел числовой последовательности.
2. Теорема Вейерштрасса.
3. Бесконечно малые последовательности.
4. Бесконечно большие последовательности.
5. Предел функции.
6. Первый замечательный предел.
7. Второй замечательный предел.
8. Эквивалентные бесконечно малые.
9. Точка разрыва функции 1-го рода.
10. Точка разрыва функции 2-го рода.
Задания
1. Вычислить пределы функций:
| № | Пределы | № | Пределы |
а) 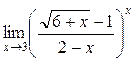 ; б) ; б)  ; в) ; в) 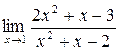 ; г) ; г) 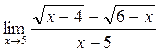 ; д) ; д) 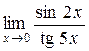 ; е) ; е) 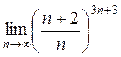 . . | а) 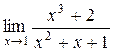 ; б) ; б) 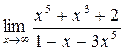 ; в) ; в) 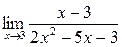 ; г) ; г) 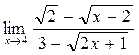 ; д) ; д) 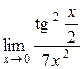 ; е) ; е) 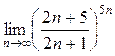 . . | ||
а) 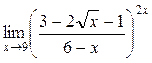 ; б) ; б) 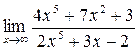 ; в) ; в) 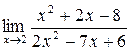 ; г) ; г) 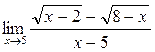 ; д) ; д) 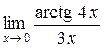 ; е) ; е) 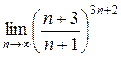 . . | а) 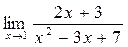 ; б) ; б) 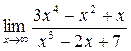 ; в) ; в) 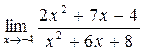 ; г) ; г) 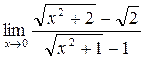 ; д) ; д) 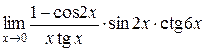 ; е) ; е) 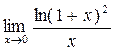 . . | ||
а) 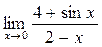 ; б) ; б)  ; в) ; в) 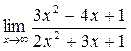 ; г) ; г)  ; д) ; д) 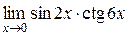 ; е) ; е) 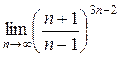 . . | а) 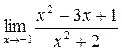 ; б) ; б) 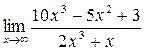 ; в); ; в); 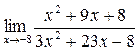 ; г) ; г) 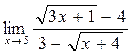 ; д) ; д) 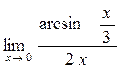 ; е) ; е) 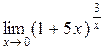 . . | ||
а) 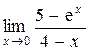 ; б) ; б)  ; в) ; в) 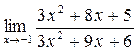 ; г) ; г) 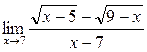 ; д) ; д) 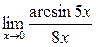 ; е) ; е) 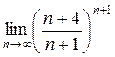 . . | а) 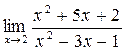 ; б) ; б) 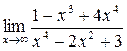 ; в) ; в) 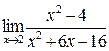 ; г) ; г) 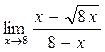 ; д) ; д) 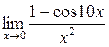 ; е) ; е) 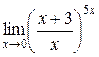 . . | ||
а) 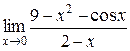 ; б) ; б) 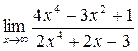 ; в) ; в) 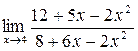 ; г) ; г) 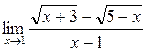 ; д) ; д) 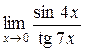 ; е) ; е) 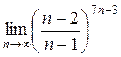 . . | а) 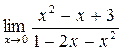 ; б) ; б) 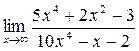 ; в) ; в) 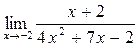 ; г) ; г) 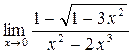 ; д) ; д) 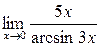 ; е) ; е) 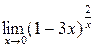 . . | ||
а) 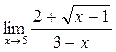 ; б) ; б) 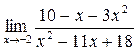 ; в) ; в) 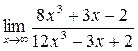 ; г) ; г) 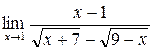 ; д) ; д) 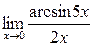 ; е) ; е)  . . | а) 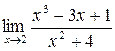 ; б) ; б) 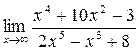 ; в) ; в) 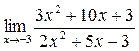 ; г) ; г)  ; д) ; д) 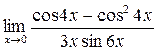 ; е) ; е) 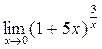 . . | ||
а) 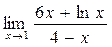 ; б) ; б) 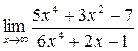 ; в) ; в)  ; г) ; г) 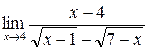 ; д) ; д) 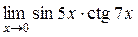 ; е) ; е) 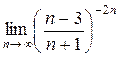 . . | а) 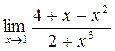 ; б) ; б) 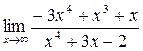 ; в) ; в) 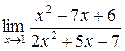 ; г) ; г) 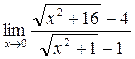 ; д) ; д) 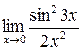 ; е) ; е) 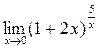 . . | ||
а) 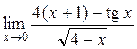 ; б) ; б) 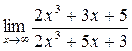 ; в) ; в) 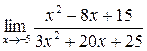 ; г) ; г) 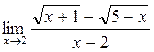 ; д) ; д) 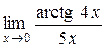 ; е) ; е) 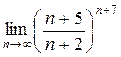 . . | а) 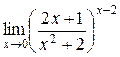 ; б) ; б) 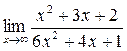 ; в) ; в) 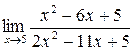 ; г) ; г) 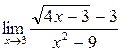 ; д) ; д) 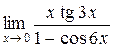 ; е) ; е) 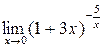 . . | ||
а) 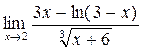 ; б) ; б) 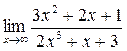 ; в) ; в) 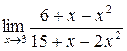 ; г) ; г) 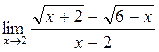 ; д) ; д) 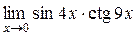 ; е) ; е) 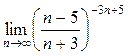 . . | а) 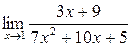 ; б) ; б) 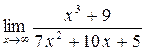 ; в) ; в) 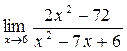 ; г) ; г) 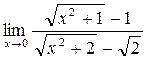 ; д) ; д) 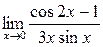 ; е) ; е) 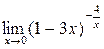 . . | ||
а) 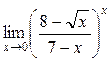 ; б) ; б) 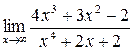 ; в) ; в) 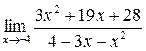 ; г) ; г) 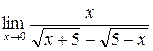 ; д) ; д) 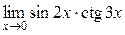 ; е) ; е) 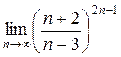 . . | а) 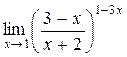 ; б) ; б) 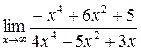 ; в) ; в) 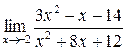 ; г) ; г) 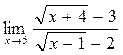 ; д) ; д)  ; е) ; е) 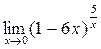 . . | ||
а) 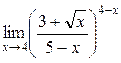 ; б) ; б) 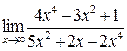 ; в) ; в) 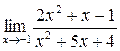 ; г) ; г) 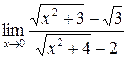 ; д) ; д) 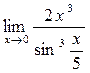 ; е) ; е)  . . | а) 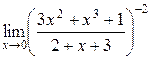 ; б) ; б) 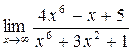 ; в) ; в) 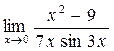 ; г) ; г) 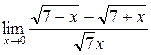 ; д) ; д) 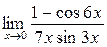 ; е) ; е) 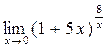 . . | ||
а) 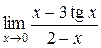 ; б) ; б)  ; в) ; в) 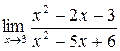 ; г) ; г)  ; д) ; д)  ; е) ; е)  . . | а)  ; б) ; б) 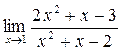 ; в) ; в) 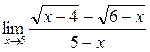 ; г) ; г) 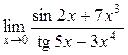 ; д) ; д) 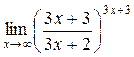 ; е) ; е) 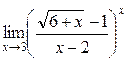 . . | ||
а) 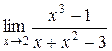 ; б) ; б) 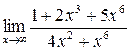 ; в) ; в) 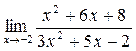 ; г) ; г) 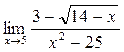 ; д) ; д) 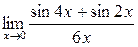 ; е) ; е) 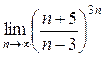 . . | а) 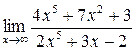 ; б) ; б) 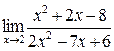 ; в) ; в) 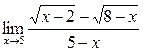 ; г) ; г)  ; д) ; д) 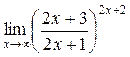 ; е) ; е) 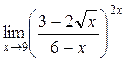 . . | ||
а) 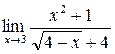 ; б) ; б) 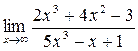 ; в) ; в) 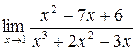 ; г) ; г) 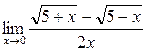 ; д) ; д) 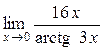 ; е) ; е) 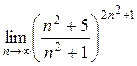 . . | а) 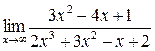 ; б) ; б)  ; в) ; в) 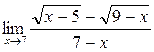 ; г) ; г) 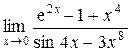 ; д) ; д) 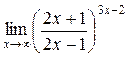 ; е) ; е) 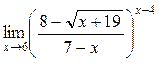 . . | ||
а) 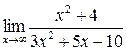 ; б) ; б) 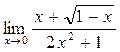 ; в) ; в) 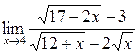 ; г) ; г)  ; д) ; д) 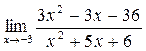 ; е) ; е) 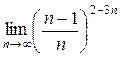 . . | а) 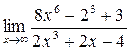 ; б) ; б) 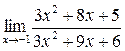 ; в) ; в) 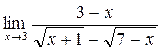 ; г) ; г) 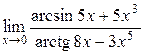 ; д) ; д) 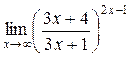 ; е) ; е) 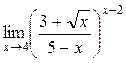 . . |
2. Исследовать функцию f(x) на непрерывность, установить тип точек разрыва и построить график функции в окрестности точек разрыва:
| № | Функция f(x) | № | Функция f(x) |
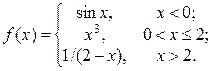 |  | ||
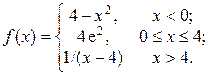 | 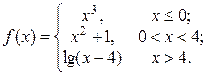 | ||
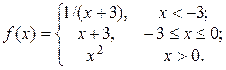 | 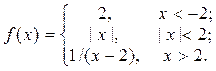 | ||
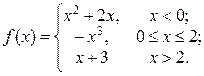 | 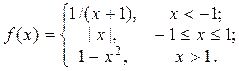 | ||
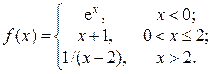 | 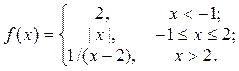 | ||
 | 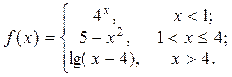 | ||
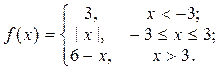 | 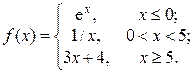 | ||
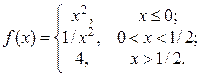 | 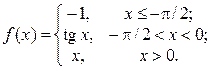 | ||
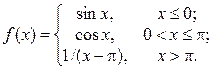 | 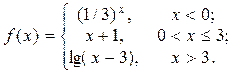 | ||
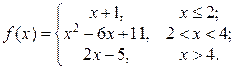 | 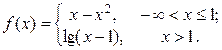 | ||
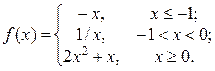 | 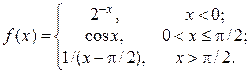 | ||
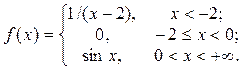 | 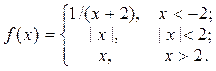 | ||
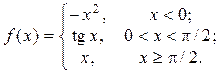 | 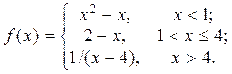 | ||
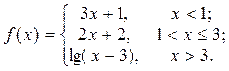 | 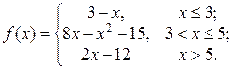 | ||
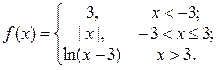 |  |
Справочный материал
к 7-й лабораторной работе
1. Функция (числовая функция)у = у(х) – зависимость переменной у от переменной х, при которой каждому значению х Î 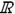 соответствует единственное значение у; независимая переменная х называется аргументом функции.
соответствует единственное значение у; независимая переменная х называется аргументом функции.
2. Числовая последовательность– функция, областью определения которой является множество натуральных чисел; числовая последовательность обозначается как {un}, n Î 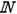 .
.
3. Монотонная числовая последовательность – возрастающаяпоследовательность (т.е. последовательность {un}, в которой un £ un +1 для всех п) или убывающая последовательность (т.е. последовательность {un}, в которой un £ un +1 для всех п).
4. Ограниченная числовая последовательность– последовательность {un}, для которой существует такое число С Î 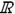 , что |un| £Cдля всех n.
, что |un| £Cдля всех n.
5. Предел числовой последовательности{un} – такое конечное число А, что с ростом п величина |un– A| сколь угодно близко приближается к нулю, т.е. для любого сколь угодно маленького числа ε > 0, начиная с некоторого номера N(т.е. при n³N) будет выполняться неравенство |un– A| < ε; обозначение предела числовой последовательности: 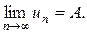
6. Теорема Вейерштрасса: если, начиная с некоторого номера N, последовательность монотонна и ограничена, то она имеет предел.
7. Сходящейся числовая последовательность– последовательность {un}, имеющая конечный предел; неограниченно возрастающая монотонная последовательность (обозначение: 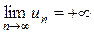 ), неограниченно убывающая монотонная последовательность (обозначение:
), неограниченно убывающая монотонная последовательность (обозначение: 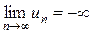 ) и последовательность, для которой предела не существует, называется расходящейся.
) и последовательность, для которой предела не существует, называется расходящейся.
8. Бесконечно большие последовательности– последовательности {un}, для которых 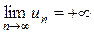 или
или 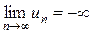 ; обозначение бесконечно больших последовательностей:
; обозначение бесконечно больших последовательностей: 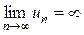 .
.
9. Бесконечно малые последовательности – последовательности {un}, для которых 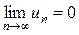 .
.
10. Предел функции у = у(х) в точке х = х0 – такое конечное число А, что для любой бесконечной последовательности точек {xn} на оси х, сходящейся к точке х = х0, т.е. когда 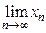 = х0, соответствующая последовательность {yn = y(хn)} сходится к точке y = А, т.е. когда
= х0, соответствующая последовательность {yn = y(хn)} сходится к точке y = А, т.е. когда 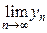 = А; обозначение предела функции у = у(х) в точке х = х0:
= А; обозначение предела функции у = у(х) в точке х = х0: 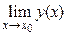 = А. Число А называется пределом функции y = y(x)при х ® + ∞, если с ростом х значение функции подходит как угодно близко к А:
= А. Число А называется пределом функции y = y(x)при х ® + ∞, если с ростом х значение функции подходит как угодно близко к А: 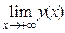 = А; если же при х ® – ∞, значение функции y = y(x)стремится к числу В, то
= А; если же при х ® – ∞, значение функции y = y(x)стремится к числу В, то 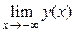 = В; если А = В, то обозначение предела функции:
= В; если А = В, то обозначение предела функции: 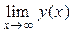 =
= 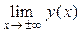 = А.
= А.
11. Бесконечно большая – функция y= y(х), для которой 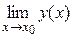 = ∞, где х0 – конечное число или ∞ (т.е. один из символов + ∞, или – ∞).
= ∞, где х0 – конечное число или ∞ (т.е. один из символов + ∞, или – ∞).
12. Бесконечно малая в окрестности точки х = х0 – функция y= y(х), для которой 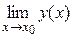 = 0, где х0 – конечное число; бесконечно малая на бесконечности – функция y= y(х), для которой
= 0, где х0 – конечное число; бесконечно малая на бесконечности – функция y= y(х), для которой 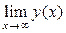 = 0, где ¥ один из символов + ∞, или – ∞.
= 0, где ¥ один из символов + ∞, или – ∞.
13. Бесконечно малые одного порядка в окрестности точки х0 – бесконечно малые у1(х) и у2(х), предел отношения которых в точке х = х0 равен конечному числу А ≠ 0; если 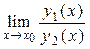 = 0, то у1(х) называется бесконечно малой более высокого порядка, чем у2(х), что обозначается как: у1(х) = ο(у2(х)).
= 0, то у1(х) называется бесконечно малой более высокого порядка, чем у2(х), что обозначается как: у1(х) = ο(у2(х)).
14. Эквивалентные бесконечно малыев окрестности точки х = х0 – бесконечно малые у1(х) и у2(х), предел отношения которых в точке х = х0 равен 1 (обозначение эквивалентных малых: у1(х) ~ у2(х)). Примеры эквивалентных малых в окрестности точки х = 0: sin α(х) ~ tg α(х) ~ arcsin α(х) ~ arctg α(х) ~ eα(х) – 1 ~ α(х); a α(х) – 1 ~ α(х)·ln a; ln(1 ± α(х)) ~ ± α(х); loga(1 ± α(х)) ~ 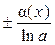 ; (1 ± α(х))a – 1 ~ ± a·α(х); 1 – cos α(х) ~
; (1 ± α(х))a – 1 ~ ± a·α(х); 1 – cos α(х) ~ 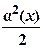 .
.
15. Таблица некоторых пределов функций:
| №№ п/п | Пределы | Примечания |
| 1. | 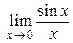 = = 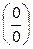 = 1 = 1 | 1-й замечательный предел |
| 2. | 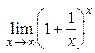 = (1∞) = е; = (1∞) = е; 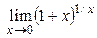 = (1∞) = е = (1∞) = е | 2-й замечательный предел, е » 2,7183 |
| 3. | 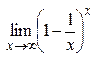 = (1∞) = = (1∞) = 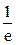 ; ; 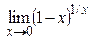 = (1∞) = = (1∞) = 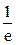 | |
| 4. | 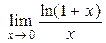 = = 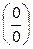 = 1; = 1; 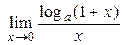 = = 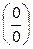 = = 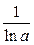 | 0 < a < + ¥, a ≠ 1 |
| 5. | 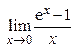 = = 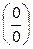 = 1; = 1;  = = 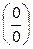 = ln a = ln a | 0 < a < + ¥, a ≠ 1 |
| 6. | 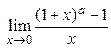 = = 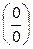 = a = a | a ≠ 0 |
| 7. | 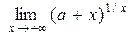 = (∞0) = 1 = (∞0) = 1 | – ∞ < a < + ∞ |
| 8. | 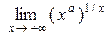 = 1, в частности, = 1, в частности, 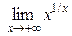 =1 =1 | – ∞ < a < + ∞; неопределенность типа ∞0 при 0 < a < + ¥ и типа 00 при – ¥ < а < 0 |
| 9. |  = 1 = 1 | 0 < a < 1; неопределенности нет: 10 = 1 |
| 10. |  = 1 = 1 | 0 < a < + ¥; неопределенности нет: С0 = 1 |
| 11. | 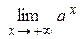 = 0; = 0; 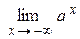 = + ∞ = + ∞ | 0 < a < 1 |
| 12. | 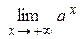 = +∞; = +∞; 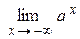 = 0 = 0 | 1 < a < + ¥ |
| 13. | 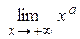 = + ∞ = + ∞ | 0 < a < + ¥ |
| 14. | 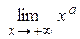 = 0 = 0 | – ¥ < а < 0 |
| 15. | 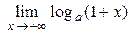 = – ∞ = – ∞ | 0 < a < 1 |
| 16. | 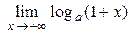 = + ∞ = + ∞ | 1 < a < + ¥ |
16. Методы вычисления предела функции 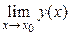 :
:
Ø заменить аргумент функции х его предельным значением х0, используя свойства непрерывных функций: 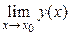 = у(х0), где х0 внутренняя или граничная точка области определения непрерывной функции у = у(х): если в результате получено конечное число А или бесконечное значение предела (+ ∞ или – ∞), то предел найден;
= у(х0), где х0 внутренняя или граничная точка области определения непрерывной функции у = у(х): если в результате получено конечное число А или бесконечное значение предела (+ ∞ или – ∞), то предел найден;
Ø если у(х0) представляет неопределенность, то использовать методы ее раскрытия:
– для раскрытия неопределенностей вида 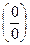 и
и  (при этом
(при этом 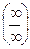 можно свести к
можно свести к 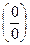 , т.к. отношение бесконечно больших β1/β2 в силу β1 = 1/α1 и β2 = 1/α2, где α1 и α2 – бесконечно малые, можно заменить отношением α2/ α1 = β1/β2):
, т.к. отношение бесконечно больших β1/β2 в силу β1 = 1/α1 и β2 = 1/α2, где α1 и α2 – бесконечно малые, можно заменить отношением α2/ α1 = β1/β2):
а)использовать пределы в приведенной таблице непосредственно или после выполнения определенных тождественных преобразований и замены переменной с целью выделения бесконечно малой; в частности, для некоторых выражений, содержащих тригонометрические функции, указанные операции могут привести к 1-му замечательному пределу;
б) если в числителе и (или) в знаменателе функции у(х) многочлены, то: при х ® 0 оставить в каждом многочлене член с переменной х в минимальной степени; при х ® ∞ оставить в каждом многочлене член с переменной х в максимальной степени; при х ® х0 выделить в каждом многочлене множитель (х – х0), представляющий бесконечно малую величину;
в) в числителе и знаменателе функции использовать эквивалентные бесконечно малые;
г)если бесконечно малой является разность, содержащая корни, то следует эту разность умножить и разделить на такое выражение, которое с учетом формул сокращенного умножения позволит вывести бесконечную малую из иррациональности;
Ø для раскрытия неопределенностей вида(0·∞)и(∞ – ∞)можно, если удастся, непосредственно выполнить операции умножения и вычитания, или сначала преобразовать неопределенности к виду 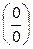 или
или 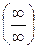 , а затем использовать приемы а) – г);
, а затем использовать приемы а) – г);
Ø для раскрытия неопределенности вида(1∞) нужно использовать 2-й замечательный предел (см. таблицу пределов) или формулу, получаемую как следствие этого предела: 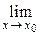 у(х) =
у(х) = 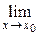 u(x)β(x) = (1∞) = exp[
u(x)β(x) = (1∞) = exp[ 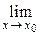 (β(x)·(u(x) – 1))];
(β(x)·(u(x) – 1))];
Ø для раскрытия неопределенности вида(00)и(∞0) рекомендуется предварительно вычислить предел натурального логарифма функции 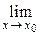 lnу(х) = A, а затем воспользоваться равенством
lnу(х) = A, а затем воспользоваться равенством 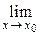 у(х) =
у(х) = 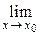 e ln y(x) =
e ln y(x) = 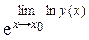 = е А.
= е А.
Примечание:при вычислении пределов числовых последовательностей можно воспользоваться равенством: 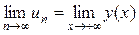 , если заменить п на непрерывную переменную х, а функцию un= u(n) на у(х).
, если заменить п на непрерывную переменную х, а функцию un= u(n) на у(х).
17. Свойства пределов:
1) предел постоянной у(х) = С равен этой постоянной: 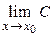 = С.
= С.
2) 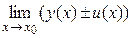 =
= 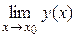 ±
± 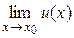 [для непрерывных в точке х0функций
[для непрерывных в точке х0функций 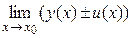 = у(х0) + и(х0)];
= у(х0) + и(х0)];
3)  =
= 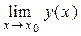 ·
· 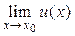 [для непрерывных в точке х0функций
[для непрерывных в точке х0функций  = у(х0) · и(х0)];
= у(х0) · и(х0)];
4) 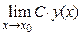 =
= 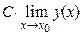 [для непрерывной в точке х0 функции
[для непрерывной в точке х0 функции 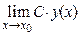 = C·у(х0)];
= C·у(х0)];
5) 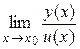 =
= 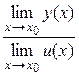 [для непрерывных в точке х0функций
[для непрерывных в точке х0функций 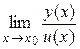 = у(х0)/и(х0), если и(х0)≠ 0];
= у(х0)/и(х0), если и(х0)≠ 0];
6) 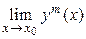 = (
= ( 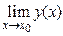 )m[для непрерывной в точке х0 функции
)m[для непрерывной в точке х0 функции 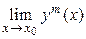 = уm(х0)];
= уm(х0)];
7) 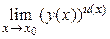 =
= 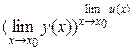 [для непрерывных в точке х0функций
[для непрерывных в точке х0функций 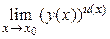 = у(х0)u(x0)].
= у(х0)u(x0)].
18. Односторонние пределы: предел функции у = у(х), получаемый для любой сходящейся к х0 последовательности {xn} при условии, что все xn< x0, называется пределом слева (обозначение предела слева точки х0: 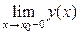 = у(х0 – 0) = А); предел функции у = у(х), получаемый для любой сходящейся к х0 последовательности {xn} при условии, что все xn > x0, называется пределом справа (обозначение предела справа точки х0:
= у(х0 – 0) = А); предел функции у = у(х), получаемый для любой сходящейся к х0 последовательности {xn} при условии, что все xn > x0, называется пределом справа (обозначение предела справа точки х0: 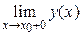 = у(х0 + 0) = В).
= у(х0 + 0) = В).
19. Условие непрерывности функцииу = у(х)в точкех = х0: у(х0 – 0) = у(х0 + 0) = у(х0).
20. Точка разрыва 1-го рода – точка х0, в которой правый и левый пределы функции y = y(х) конечны, но не равны друг другу, или, в случае их равенства, сама функция y = y(х) не определена в точке х0 или ее значение в этой точке у(х0) ¹ у(х0 – 0) = у(х0 + 0).
21. Точка разрыва 2-го рода – точка х0, в которой хотя бы один из односторонних пределов функции y = y(х) равен бесконечности (+ ¥ или – ¥) или не существует.
