Условные развертки неразвертывающихся поверхностей

Рассмотрим несколько примеров, следуя указанной ранее схеме построения условной развертки поверхности.

Задача. Дана поверхность вращения (рис. 13.10). Построить ее развертку. Очевидно, данная поверхность не является развертывающейся и для нее можно построить лишь условную развертку. Разделим поверхность вращения осевыми плоскостями Δⁱ, где i = 1, 2, 3, …, на равное число частей (отсеков) и выберем одну из них (например, шестую часть), ограниченную проецирующими плоскостями Δ¹ и Δ² , имеющими горизонтальные следы Δ₁¹ и Δ₂¹. Примем очерковую линию t(t₁, t₂) за направляющую линию цилиндрической поверхности с отрезками ее фронтально - проецирующих образующих между плоскостями Δ¹ и Δ².

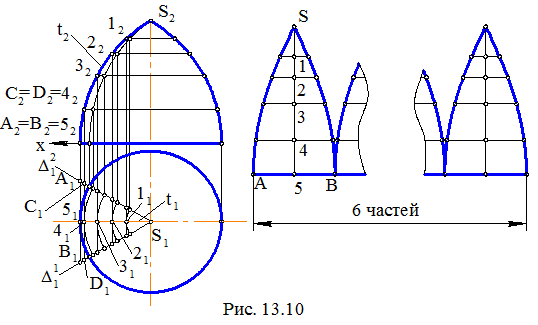
Отсеком этой поверхности выполнена аппроксимация выбранной части исходной поверхности. В соответствии со схемой построения условной развертки выполним вторую аппроксимацию, заменив отсек цилиндрической поверхности отсеком призматической поверхности. Для этого выберем на направляющей t ряд точек, например S, 1, 2, 3, 4, 5, и проведем через них фронтально проецирующие образующие, например, АВ ' 5. Отрезки этих прямолинейных образующих между осевыми плоскостями Δ¹ и Δ² заменяют соответствующие отрезки параллелей (окружностей) исходной поверхности и являются ребрами призматической поверхности, а ломаная линия S12345, вписанная в линию t , является направляющей линией этой поверхности. Точная развертка призматической поверхности, вписанной в цилиндрическую поверхность, будет служить приближенной разверткой описанной цилиндрической поверхности и условной разверткой отсека исходной поверхности вращения. Для построения развертки отсека вписанной призматической поверхности проведем в стороне от исходного КЧ горизонтальную линию и выберем на ней точку 5. По обе стороны от точки 5 отметим горизонтально и симметрично точки А и В такие, что АВ = А₁В₁. Вертикально от точки А отложим отрезок 54 = 5₂4₂. Затем от точки 4 горизонтально и симметрично отметим точки С и D такие, что CD = C₁D₁ и т. д. В итоге построений получаем два ряда тачек, симметричных относительно линии 5S. Соединив точки каждого ряда лекальными кривыми, получим условную развертку выделенного отсека исходной поверхности. Присоединив к ней такие же (равные) развертки остальных отсеков, получим полную условную развертку поверхности.

Задача. Дана четверть поверхности тора (рис. 13.11). Построить ее развертку.

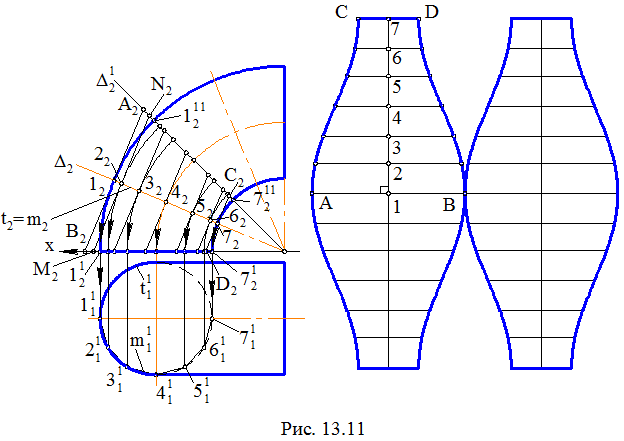Для решения задачи рассечем четверть поверхности тора фронтально проецирующими осевыми плоскостями Δⁱ, i = 1, 2, 3… на равные отсеки и выделим один из них, например заключенный между секущими плоскостями П₁ и Δ¹ . Проведем плоскость симметрии Δ этого отсека. Она рассекает отсек тора по окружности t , при этом t₂ = 1₂7₂, где t₁¹ – НВ этой окружности. Заменим выделенный отсек поверхности четверти тора отсеком описанной цилиндрической поверхности с направляющей t и образующими – фронтальными линиями уровня, заключенными между плоскостями П₁ и Δ¹. Отрезки этих образующих в пределах между П₁ и Δ¹ заменяют отрезки соответствующих параллелей (окружностей) поверхности четверти тора. Например отрезок АВ(А₂В₂) прямой заменяет дугу параллели 1¹1¹¹(1₂¹1₂¹¹), отрезок CD(C₂D₂) заменяет дугу параллели 7¹7¹¹(7₂¹7₂¹¹) и т. д. После этого заменим отсек описанной цилиндрической поверхности отсеком призматической поверхности, вписанной в цилиндрическую.

Линия m (m₂) – ломаная линия, вписанная в окружность t и проходящая через вершины 1, 2, 3, 4, 5, 6, 7. Эта линия служит направляющей вписанной призматической поверхности и имеет своей НВ ломаную линию m₁¹, проходящую через вершины 1₁¹, 2₁¹,…, 7₁¹ . Образующие АВ, …, CD цилиндрической поверхности являются ребрами призматической поверхности. Точная развертка отсека вписанной призматической поверхности является приближенной разверткой отсека описанной цилиндрической поверхности и условной разверткой отсека поверхности тора. Для построения условной развертки отметим в стороне от КЧ на горизонтальной прямой точку 1 и симметричные точки А и В такие, что АВ =

= А₂В₂ . На вертикальной прямой на точке 1 отложим отрезок 12 = 1₁¹2₁¹ и проведем через точку 2 горизонтальную прямую, на которой построим симметричные точки M и N так, что MN = M₂N₂ и т. д. В итоге построений получим два вертикально симметричных точечных ряда A, N, …C и B, M,…, D. Отразив их симметрично относительно горизонтальной прямой АВ и проведя через каждый из них лекальную кривую, получим условную развертку выделенного отсека поверхности тора. Добавив к ней такие же (равные) развертки остальных отсеков, получим полную условную развертку четверти поверхности тора или же всей его поверхности.

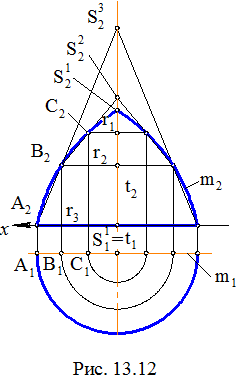Задача. Дана поверхность вращения с осью вращения t и образующей кривой m (рис.13.12). Построить ее развертку.

Очевидно, данная поверхность может иметь только условную развертку. Для ее построения можно применить метод конусов. Решение задачи в этом случае может быть следующим:

1) заменяем образующую m ломаной линией

ABCS¹(A₁ B₁ C₁ S¹₁, A₂ B₂ C₂ S¹₂);

2) рассекаем заданную поверхность вращения плоскостями, перпендикулярными оси t и проходящими через вершины ломаной;

3) образующиеся в сечениях окружности принимаем в качестве оснований конических поверхностей с вершинами и радиусами

оснований: S¹, r₁; S², r₁; S², r₂; S³, r₂; S³, r₃;

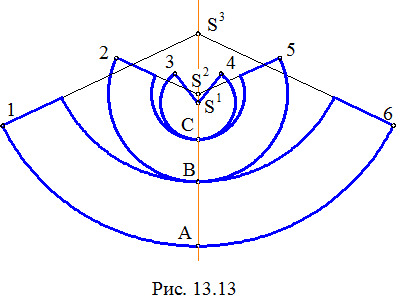4) для каждой конической поверхности строим ее точную развертку на основе ранее приведенной формулы a_i = 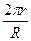, где r принимает значения r₁, r₂, r₃; R принимает значения S¹C, S²C, S²B, S³B, S³A; a₁ = Ð3S¹4, a₂ = = Ð2S²5, a₃ = 1 S³6.

В итоге построений получаем условную развертку исходной поверхности вращения, составленную из трех точных разверток таких конических поверхностей: полной S¹, r₁ и двух усеченных поверхностей

S², r₁, r₂; S³, r₂, r₃.