Описание экспериментальной установки
Лабораторная работа выполняется на стенде Ф-01 ЭиМ «Электричество и магнетизм» (рис.5.2).

Рис.5.2. Внешний вид стенда Ф-01 ЭиМ
Элекрическая схема работы представлена на рис.5.3. Трансформатор однофазный, с двумя вторичными обмотками с числом витков 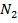 и
и 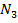 . При замкнутом ключе
. При замкнутом ключе 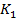 и разомкнутом
и разомкнутом 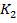 исследуется режим холостого хода трансформатора. При замкнутых ключах
исследуется режим холостого хода трансформатора. При замкнутых ключах 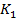 и
и 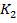 исследуется рабочий режим трансформатора.
исследуется рабочий режим трансформатора.

Рис.5.3.Электрическая схема установки.
Порядок выполнения работы.
1. Собрать электрическую схему согласно рис.5.3.
2. Ключ 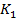 замкнуть,
замкнуть, 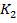 разомкнуть. Вольтметром изменить напряжение на концах первичной и вторичных обмоток. Результаты измерений занести в таблицу 1.
разомкнуть. Вольтметром изменить напряжение на концах первичной и вторичных обмоток. Результаты измерений занести в таблицу 1.
Таблица № 1. Результаты измерений
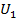 , B , B | 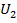 , B , B | 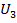 , B , B | Число витков | коэф. трансформации | ||||
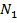 | 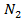 | 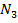 | 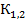 | 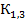 | ||||
3. Определить число витков вторичных обмоток трансформатора по формулам:
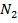 =
= 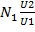 ;
; 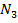 =
= 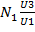
4. Вычислить коэффициенты трансформации по формулам:
К1,2= 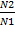 ;K1,3 =
;K1,3 = 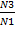
Результаты измерений занести в таблицу № 1.
5. Замкнуть ключ 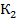 . Для 5 - 6 положений движка реостата измерить напряжения
. Для 5 - 6 положений движка реостата измерить напряжения 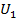 ,
, 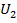 и силу тока
и силу тока 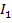 ,
, 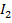 в обмотках 1 и 2 трансформатора. Результаты измерений занести в таблицу №2.
в обмотках 1 и 2 трансформатора. Результаты измерений занести в таблицу №2.
Таблица№2. Результаты измерений
| № | 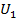 , B , B | 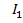 , A , A | 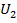 , B , B | 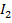 , A , A | 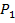 , Вт , Вт | 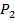 , Вт , Вт | 𝜂,% |
6. Для каждого зафиксированного положения движка реостата рассчитать мощность электрического тока в первичной и вторичной обмотках, а также КПД трансформатора по формулам:
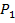 =
= 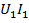 ;
; 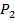 =
= 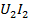 , 𝜂 =
, 𝜂 = 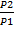 100%.
100%.
Результаты вычислений занести в таблицу №2.
7. Построить график зависимости 𝜂 от потребляемой мощности 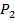 во вторичной обмотке.
во вторичной обмотке.
8.Сформулировать выводы по выполненной работе.
Контрольные вопросы
1. Что такое трансформатор и для чего он предназначен?
2.Что такое автотрансформатор?
3.Что такое коэффициент трансформации?
4. От чего зависит КПД трансформатора?
ЛАБОРАТОРНАЯ РАБОТА № 4.1
ИЗУЧЕНИЕ СВОБОДНЫХ ЗАТУХАЮЩИХ КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА
Цель работы: Ознакомиться с методикой исследования свободных затухающих колебаний, определить логарифмический декремент затухания колебаний и коэффициент вязкого сопротивления колебаниям.
Приборы и принадлежности
1. Штатив.
2. Сосуд с жидкостью.
3. Набор пружин и грузов.
4. Секундомер.
5. Линейка.
6. Рячажные весы.
Теоретическое введение
Пусть груз массой m подвешен на пружине с жесткостью k (рисунок 7.1). В положении статического равновесия сила тяжести груза mg уравновешивается силой упругости kλст, т.е.
mg = kλст,
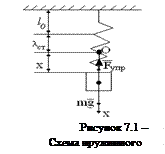 где λст – статическое удлинение пружины.
где λст – статическое удлинение пружины.
 В этом положении пружинного маятника (в точке О) помещаем начало отсчета, и ось х направляем в сторону удлинения пружины. Второй закон Ньютона в проекции на ось Ох в произвольный момент времени имеет вид
В этом положении пружинного маятника (в точке О) помещаем начало отсчета, и ось х направляем в сторону удлинения пружины. Второй закон Ньютона в проекции на ось Ох в произвольный момент времени имеет вид
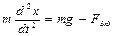 где
где 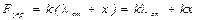 .
.
Тогда 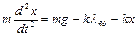 , или
, или 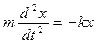 ,
,
или 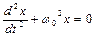 , (7.1)
, (7.1)
где 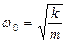 – круговая (циклическая) частота свободных незатухающих колебаний пружинного маятника (собственная частота).
– круговая (циклическая) частота свободных незатухающих колебаний пружинного маятника (собственная частота).
Уравнение (7.1) – это дифференциальное уравнение свободных незатухающих колебаний, общее решение которого имеет вид
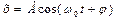 . (7.2)
. (7.2)
График гармонических колебаний представлен на рисунке 7.2.
Здесь А – амплитуда колебаний (наибольшее смещение груза от равновесного положения), Т0 – период колебаний, который с частотой υ и круговой частотой ω0 связан соотношением
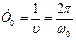 . (7.3)
. (7.3)
 Отсюда следует, что если частота колебаний υ численно равначислу колебаний за 1 секунду, то круговая частота ω0 равна числу колебаний за 2π секунд.
Отсюда следует, что если частота колебаний υ численно равначислу колебаний за 1 секунду, то круговая частота ω0 равна числу колебаний за 2π секунд.
Из вышеуказанного следует, что в случае вертикального расположения пружинного маятника уравнения (7.1) и (7.2) имеют тот же вид, что и при горизонтальном расположении маятника. При вертикальном расположении маятника на груз действует постоянная во времени сила тяжести mg, которая смещает положение равновесия, около которого происходят гармонические колебания, на величину 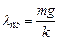 .
.
В случае, когда колебания груза происходят в вязкой среде, на груз, кроме силы упругости, силы тяжести и выталкивающей силы Архимеда, действует еще сила вязкого трения Fтр = γV, которая пропорциональна скорости движения 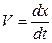 и направлена в сторону, противоположную движению груза. Здесь γ – коэффициент вязкого сопротивления колебаниям, который зависит от размеров и формы тела. Второй закон Ньютона в проекции на ось Ох имеет вид
и направлена в сторону, противоположную движению груза. Здесь γ – коэффициент вязкого сопротивления колебаниям, который зависит от размеров и формы тела. Второй закон Ньютона в проекции на ось Ох имеет вид
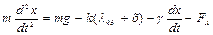 , (7.4)
, (7.4)
где 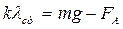 .
.
После преобразований получаем дифференциальное уравнение затухающих колебаний
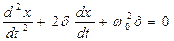 , (7.5)
, (7.5)
где 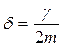 – коэффициент затухания, [δ] = с-1,
– коэффициент затухания, [δ] = с-1,
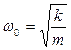 – собственная круговая частота.
– собственная круговая частота.
В случае малого сопротивления, когда δ < ω0, решение дифференциального уравнения (7.5) имеет вид
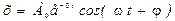 , (7.6)
, (7.6)
где А0 – начальная амплитуда колебаний,
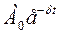 – убывающая со временем амплитуда колебаний,
– убывающая со временем амплитуда колебаний,
ω – круговая частота затухающих колебаний, которая определяется по формуле
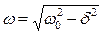 . (7.7)
. (7.7)
График функции (7.6) показан на рисунке 7.3.
Период затухающих колебаний равен
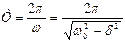 (7.8)
(7.8)
Сравнивая формулы (7.3) и (7.8), получаем, что период затухающих колебаний несколько больше периода незатухающих колебаний.
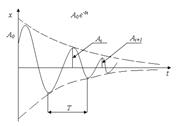
Рисунок 5.3 – График затухающих колебаний
Быстрота затухания колебаний характеризуется двумя параметрами.
1) Декрементом затухания, который равен отношению двух последовательных амплитудных отклонений системы в одну сторону от равновесного состояния (рисунок 7.3)
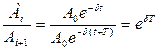 . (7.9)
. (7.9)
2) Логарифмическим декрементом затухания
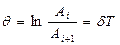 . (7.10)
. (7.10)
