Угол между прямой и плоскостью. Определение. Углом между наклонной прямой и плоскостью называется угол между

Определение. Углом между наклонной прямой и плоскостью называется угол между наклонной и ее ортогональной проекцией на эту плоскость. Если прямая параллельна плоскости или лежит в ней, то угол между прямой и плоскостью принимается равным нулю. В случае перпендикулярности прямой и плоскости угол между ними по определению равен 90°. Из определения следует, что угол между прямой и плоскостью заключен в отрезке 0 £ a £ 90°.

Задача. Даны прямая DE (рис. 9.4) и плоскость Σ(ΔАВС). Определить угол между ними.

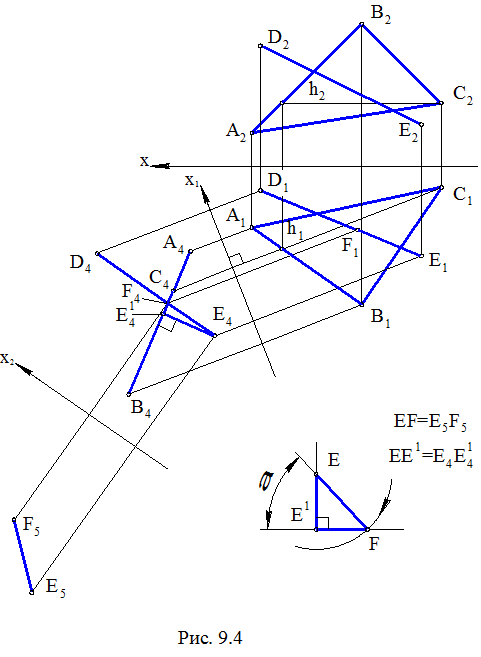
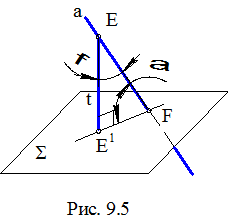Проекционное решение задачи основывается на построении прямоугольного треугольника ЕЕ¹F (рис. 9.5), в котором: EF – гипотенуза на заданной наклонной а, при этом Е – произвольная точка, F = а Ç Σ, Σ – заданная плоскость; Е¹F – катет на плоскости Σ, который представляет собой ортогональную проекцию отрезка EF; a = Ð(EF, FЕ¹ ) есть искомый угол. Рассмотрим алгоритм проекционного решения, который представлен на рисунке 9.4.

1. В плоскости Σ выбирается линия уровня, например, горизонталь h(h₁, h₂ ). При этом h₂ // x.

2. Вводится новая система плоскостей проекций П₁ , П₄ с осью x₁ ^ h₁ , такая, что П₄ ^ h .

3. На П₄ строится вырожденная проекция А₄В₄ плоскости Σ и дополнительная

проекция D₄Е₄ прямой DE.

4. Определяются дополнительные проекции F₄ и F₁ точки пересечения F = а Ç Σ,

при этом E₁F₁ , E₄F₄ – проекции гипотенузы EF в прямоугольном треугольнике

ЕЕ¹F.

5. Строится перпендикуляр Е₄Е₄¹ ^ А₄В₄ , при этом Е₄Е₄¹ = ЕЕ¹ – катет прямоугольного треугольника ЕЕ¹F.

6. Введением системы плоскостей проекций П₄, П₅ с осью x₂ // E₄F₄ и П₅ // EF определяется НВ гипотенузы EF, равная E₅F₅.

7. В стороне от проекционных построений на КЧ строится прямоугольный треугольник ЕЕ¹F по катету ЕЕ¹ и гипотенузе EF.

Угол a = Ð(E¹F, EF) является искомым.

Рассмотрим еще одно проекционное решение, основанное на треугольнике ЕЕ¹F.

Задача. Даны прямая а и плоскость Σ(ΔАВС). Определить угол между ними

(рис. 9.6).

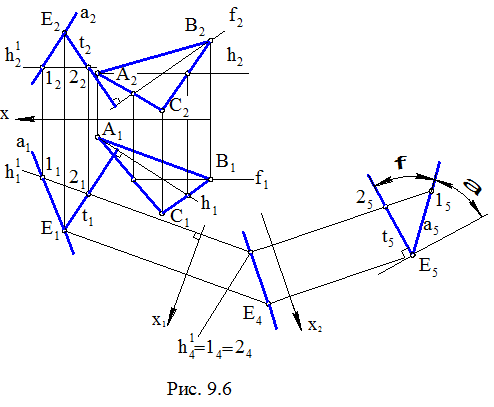
В прямоугольном треугольнике ЕЕ¹F искомый угол a может быть определен как a = 90°– j, где j – угол между прямой а, на которой расположена гипотенуза EF(см. рис. 9.5), и перпендикуляром t ^ Σ, на котором расположен катет Е₁Е¹.

Предлагаемое ниже проекционное решение данной задачи направлено на определение угла j = Ð(а, t).

1. Построим в плоскости Σ две линии уровня h(h₁, h₂ ) и f(f₁, f₂), где h₂ // х, f₁ // х.

2. Из произвольной точки Е Î а опустим перпендикуляр t ^ Σ, при этом t₂ проходит через E₂ , t₂ ^ f₂; t₁ проходит через E₁ , t₁ ^ h₁ .

3. Определяем угол j = Ð(а, t ) в следующей последовательности:

1) в плоскости Δ(а, t ) выбирается линия уровня, например, h₁(h₁¹, h₂¹ ), где

h₂¹ // х;

2) введением системы плоскостей проекций П₁ , П₄ с осью x₁ ^ h₁¹ строится на

П₄ вырожденная проекция Е₄ h₄¹ плоскости Δ;

3) введением системы плоскостей проекций П₄ , П₅ с осью x₂ // Е₄ h₄¹ строится на П₅ угол j = Ð(t₅ , а₅ );

4) построением прямого угла определяется искомый угол a = Ð(а, Σ) = 90° – j.