Загальна достатня ознака збіжності знакозмінних рядів.

Знакопочерговий ряд є окремим випадком знакозмінного ряду. Числовий ряд 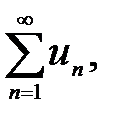що містить нескінченну множину додатніх і нескінченну множину від’ємних членів, називається знакозмінними.

Для знакозмінних рядів має місце наступна загальна достатня ознака збіжності.

Теорема. Нехай даний знакозмінний ряд

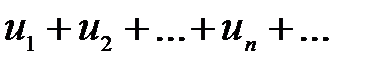
Якщо збігається ряд

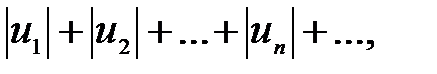
складений з модулів членів даного ряду, то збігається і сам знакозмінний ряд .

□ Розглянемо допоміжний ряд, складений з членів рядів ,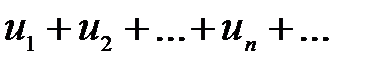

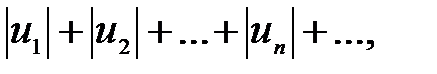
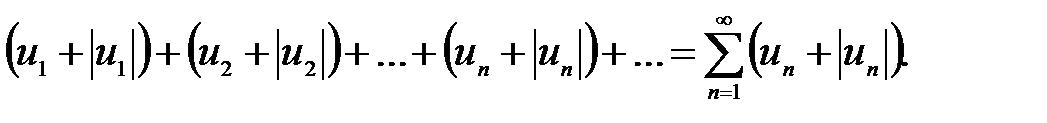
Очевидно, що 0 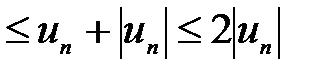для всіх 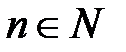. Але ряд 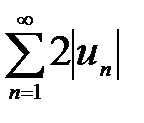збігається згідно з умовою теореми і властивості 1 числових рядів Отже, на основі ознаки порівняння збігається і ряд 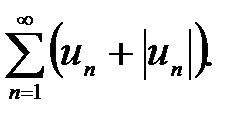Оскільки даний знакозмінний ряд є різницею двох рядів, що збігаються

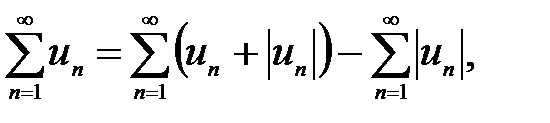
то, на основі властивості 2 числових рядів, 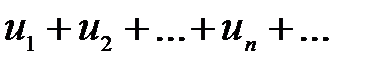збігається.

Відзначимо, що зворотне твердження несправедливе: якщо збігається ряд 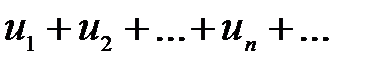,то це не означає, що сходитиметься ряд ■

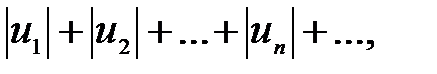Абсолютна і умовна збіжності числових рядів. Властивості рядів, що абсолютно збігаються.

Знакозмінний ряд називається тим, що абсолютно збігається, якщо ряд, складений з модулів його членів, збігається.

Знакозмінний ряд називається тим, що умовно збігається, якщо сам він збігається, а ряд, складений з модулів його членів, розбіжний. Так, ряд, показаний в прикладі (3.2), умовно збігається. Ряд .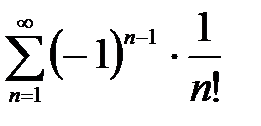

абсолютно збігається, оскільки ряд, складений змодулів його членів, збігається (див. приклад 14.2.4).

Серед знакозмінних рядів ряди, що абсолютно збігаються, займають особливе місце: на такі ряди переносяться основні властивості кінцевих сум (переставна, сполучна, розподільна).

Основні властивості рядів, що абсолютно збігаються, наводимо без доведення.

1. Якщо ряд абсолютно збігається і має суму 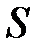, то ряд, отриманий з нього перестановкою членів, також збігається і має ту ж суму 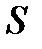, що і початковий ряд (теорема Діріхле).

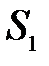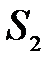2. Ряди, що абсолютно збігаються, з сумами і можна почленно додавати (віднімати). В результаті виходить ряд, що абсолютно збігається, сума якого дорівнює 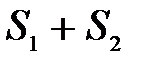(або відповідно ).

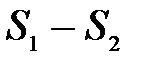3. Під добутком двох рядів 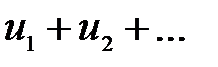і 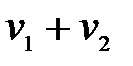розуміють ряд вигляду

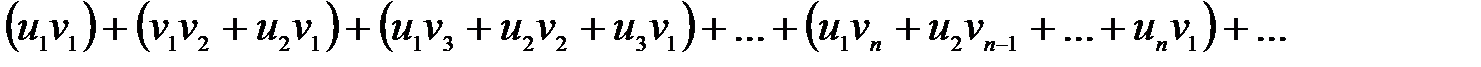
4. Добуток двох рядів, що абсолютно збігаються, з сумами 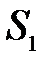і 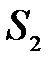є ряд, що абсолютно збігається, сума якого дорівнює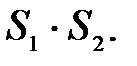

Таким чином, ряди, що абсолютно збігаються, додаються, віднімаються, перемножуються як звичайні ряди. Суми таких рядів не залежать від порядку запису членів.

У випадку рядів, що умовно збігаються, відповідні твердження (властивості), взагалі кажучи, не мають місця.

Так, переставляючи члени ряду, що умовно збігається, можна добитися того, що сума ряду зміниться. Наприклад, ряд 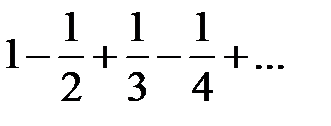умовно збігається по ознаці Лейбніца. Нехай його сума дорівнює 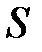. Перепишемо його члени так, що після одного позитивного члена йтимуть два негативних. Отримаємо ряд

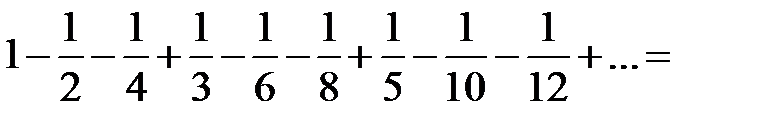
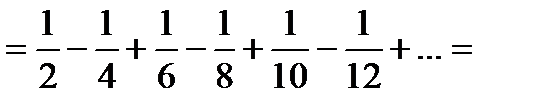
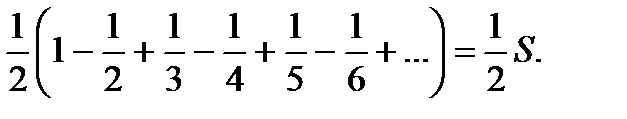
Сума зменшилася вдвічі!

Більш того, шляхом перестановки членів ряду, що умовно збігається, можна отримати ряд, що збігається, з наперед заданою сумою або ряд, що розбіжний (теорема Рімана).

Тому дії над рядами не можна виконувати, не переконавшись в їх абсолютній збіжності. Для встановлення абсолютної збіжності використовують всі ознаки збіжності знакопозитивних рядів, замінюючи усюди загальний член ряду його модулем.