Выбор лишней неизвестной и основной системы.
В предыдущем примере мы выбрали за лишнюю неизвестную реакцию В. Мы могли бы выбрать и момент 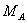 . Соответственно изменилась бы основная система и ход решения. Окончательный же результат, конечно, получился бы прежним. Возьмем за лишнюю неизвестную опорный момент
. Соответственно изменилась бы основная система и ход решения. Окончательный же результат, конечно, получился бы прежним. Возьмем за лишнюю неизвестную опорный момент 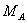 (Рис.3, а). Какой будет основная система? Чтобы получить ее, надо отбросить то опорное закрепление, которое создает момент
(Рис.3, а). Какой будет основная система? Чтобы получить ее, надо отбросить то опорное закрепление, которое создает момент 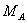 , т. е. защемление конца А. Чтобы на конце А не было опорного момента, там следует поставить шарнирно-неподвижную опору.
, т. е. защемление конца А. Чтобы на конце А не было опорного момента, там следует поставить шарнирно-неподвижную опору.
Основной системой будет балка, изображенная на Рис.3, б. Загрузим ее внешней нагрузкой и опорным моментом 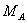 (фиг. 363, в).
(фиг. 363, в).
Чтобы эти балки работали одинаково, надо для балки Рис.3, в написать дополнительное условие, что сечение А под действием изображенных нагрузок не может поворачиваться; накладываем это ограничение на перемещение, соответствующее выбранной лишней неизвестной:
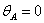
Далее, применив для решения уравнения 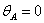 теорему Кастильяно, имеем
теорему Кастильяно, имеем
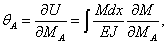
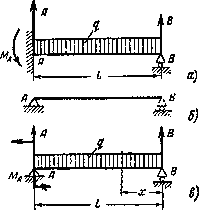
а) заданное. б) основная, в) эквивалентная
Рис.3. Расчетные схемы:
следовательно,
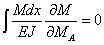
Для нахождения М и 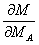 выразим реакцию В основной системы через
выразим реакцию В основной системы через 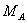 и произведем все обычные вычисления:
и произведем все обычные вычисления:
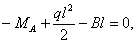
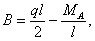
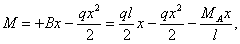
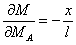 .
.
находим:
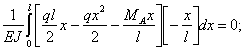
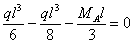
Отсюда
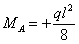 ,
,
т. е. той же величине, которая была получена раньше. Дальнейший ход решения не отличается от разобранного выше.
Решение той же основной системы (Рис.4, а) с применением способа Верещагина потребует изображения второго состояния загружения основной системы моментом 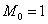 (Рис.4, б) и построения эпюр изгибающего момента: от заданной нагрузки q (Рис.4, в), от момента
(Рис.4, б) и построения эпюр изгибающего момента: от заданной нагрузки q (Рис.4, в), от момента 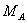 (Рис.4, г) и от единичной нагрузки;
(Рис.4, г) и от единичной нагрузки; 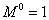 (Рис.4, д). Вычисляем
(Рис.4, д). Вычисляем 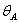 :
:
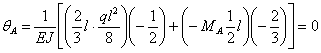

а)исходная схема, б) нагружение единичным моментом, в) грузовая эпюра, г) моментная эпюра, д) единичная эпюра моментов
Рис.4. Динамика расчета по методу Верещагина:
Как видно, уравнение для определения 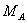 полностью совпадает с найденным по теореме Ка-стильяно.
полностью совпадает с найденным по теореме Ка-стильяно.
Сравнивая два варианта решения поставленной задачи с лишней неизвестной В и с лишней неизвестной 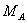 , видим, что при применении способа Кастильяно первый вариант менее сложен по вычислениям. Это объясняется тем, что основной системой в первом варианте является балка, защемленная одним концом, во втором же — балка на двух опорах; для второй — вычисления сложнее. Таким образом, лишнюю неизвестную и, следовательно, основную систему надо выбирать с таким расчетом, чтобы выкладки (вычисление изгибающих моментов и т. д.) были проще.
, видим, что при применении способа Кастильяно первый вариант менее сложен по вычислениям. Это объясняется тем, что основной системой в первом варианте является балка, защемленная одним концом, во втором же — балка на двух опорах; для второй — вычисления сложнее. Таким образом, лишнюю неизвестную и, следовательно, основную систему надо выбирать с таким расчетом, чтобы выкладки (вычисление изгибающих моментов и т. д.) были проще.
Если бы мы выбрали за лишнюю неизвестную реакцию А, то основную систему следовало бы так устроить, чтобы опора А не давала возможности поворота сечения и горизонтальных перемещений, но допускала бы вертикальные движения.
За лишнюю неизвестную нельзя брать лишь ту реакцию, при отбрасывании которой мы получим изменяемую, неустойчивую основную систему.
Общий план решения статически неопределимой задачи.
Таким образом, общий метод решения, статически неопределимых задач распадается на ряд отдельных этапов.
В дух предыдущих лекциях приведены два варианта решения задачи: с лишней реакцией В и с лишней реакцией 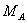 . Для развертывания добавочного условия даны также два варианта решения: способом сравнения деформаций и с применением теоремы. Кастильяно.
. Для развертывания добавочного условия даны также два варианта решения: способом сравнения деформаций и с применением теоремы. Кастильяно.
Если бы число реакций статически неопределимой балки было нe четыре, как в рассмотренном примере, а больше, то соответственно увеличилось бы число лишних неизвестных; загрузив основную систему внешней нагрузкой и этими лишними неизвестными, мы можем написать дополнительные условия, ограничивающие деформации балки в тех сечениях, где эти лишние реакции приложены. Таким путем будет получено столько же дополнительных уравнений, сколько лишних неизвестных.
Следовательно, общий метод определения добавочных опорных реакций в статически неопределимых балках основан на том, что якая дополнительная опора, вводя лишнюю неизвестную реакцию, в то же время накладывает дополнительное ограничение в основной статически определимой системе на перемещение, соответствующее лишней неизвестной реакции. Выражая уравнением это ограничение, получаем столько дополнительных уравнений, сколько добавлено новых опорных закреплений.
