Если в ходе проведения метода Гаусса появляются невыполнимые равенства типа и т.д., то исследуемая линейная система несовместна

Еще один совет: элементарные преобразования системы будут выполняться проще, если с помощью этих преобразований добиваться, чтобы коэффициенты 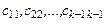, становились равными 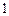или .

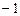Общее решение системы (2) находится так: свободным неизвестным присваивают произвольные числовые значения; затем, последовательно двигаясь от последнего уравнения системы (2) вверх к первому уравнению, определяют базисные неизвестные в порядке .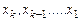

Приведем конкретные примеры применения метода Гаусса к линейным системам

Пример 2. Найти общее решение системы .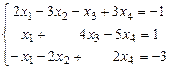

Решение. Применим метод Гаусса.

1. Поменяем местами первое и второе уравнения, получим эквивалентную систему

.

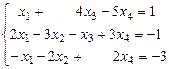2. С помощью первого уравнения исключим неизвестную 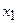из второго и третьего уравнений системы 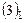. Для этого:

а) прибавим во 2-му уравнению 1-е уравнение, умноженное на число ;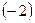

б) к 3-му уравнению прибавим 1-е уравнение.

В результате получим систему

.

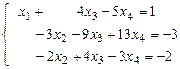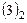
3. Два последних уравнения системы 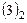образуют подсистему, независящую от неизвестной .

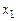Чтобы упростить последующие преобразования сделаем коэффициент 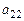, равным 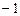. Для этого вычтем из 2-го уравнения 3-е уравнение (т.е. прибавим ко 2-му уравнению 3-е уравнение, умноженное на число 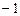). После этой операции получим систему

.

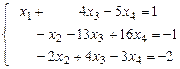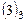
4. Теперь, в системе 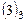с помощью 2-го уравнения исключим неизвестную 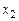из 3-го уравнения. Для этого прибавим к 3-му уравнению 2-е уравнение, умноженное на число .

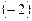В итоге получим систему треугольного вида

.

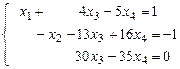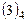
В ней 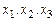- базисные неизвестные, 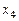- свободная неизвестная.

5. Теперь из системы 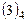найдем общее решение. Положим 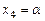, где 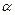- произвольное действительное число. Из 3-го уравнения находим .

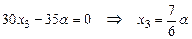Для облегчения последующих вычислений положим 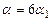, где 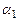, как и 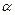, принимает произвольные действительные значения. Тогда .

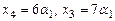Из 2-го уравнения находим .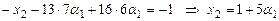

Наконец, из 1-го уравнения находим .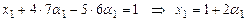

Таким образом, получен следующий результат: система 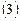совместна, и ее общее решение представимо в ви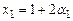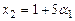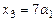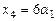де

, , , , где .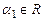

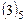
Проведем проверку. Для этого подставим найденные выражения 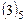неизвестных 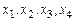во все уравнения исходной системы (3).

.

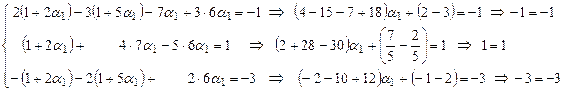Проверка подтвердила истинность решения .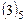

Обычно для сокращения записей метод Гаусса проводят на расширенных матрицах системы. Расширенной матрицей системы называют матрицу 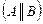, где 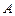- матрица системы, 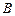- вектор столбец свободных членов. Для системы (1) расширенная матрица запишется так:

.

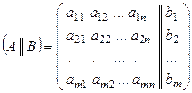1). Операция «перестановка уравнений системы» означает перестановку соответствующих строк расширенной матрицы.

2). Операция «перестановка поменять местами слагаемых с двумя выбранными неизвестными» означает перестановку соответствующих столбцов матрицы .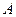

3). Операция «умножение уравнения на число, отличное от нуля» означает умножение на это число соответствующей строки расширенной матрицы.

4). Операция «прибавление к уравнению системы другого уравнения, умноженного на число» означает аналогичную операцию над строками расширенной матрицы.

Изложение метода Гаусса в примере 2 с применением расширенных матриц запишется в виде.

~ ~

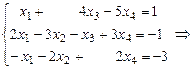
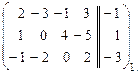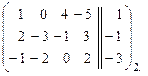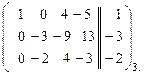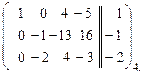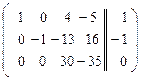
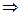~ ~ ~ система .

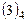Внизу, справа под матрицами указаны выполняемые над системой элементарные операции, выполненные над системой:

1. Переставили местами 1-е и 2-е уравнения.

2. Прибавили ко 2-му уравнению 1-е, умноженное на число ( ).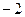

Прибавили к 3-му уравнению 1-е.

3. Прибавили ко 2-му уравнению 3-е, умноженное на число ( ).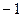

4. Прибавили к 3-му уравнению 2-е, умноженное на число ( ).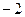

Далее находится общее решение системы (см пункт 5. решения примера 2).

Пример 3. Найти методом Гаусса общее решение системы

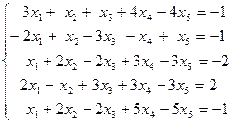
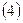
Решение проведем с использованием расширенных матриц.

~ ~ ~

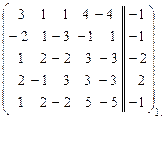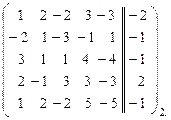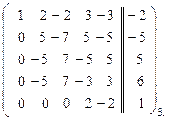1. Переставили местами 1-ю и 3-ю строки.

2. Прибавили ко 2-й строке 1-ю строку, умноженную на число 2.

Прибавили к 3-й строке 1-ю строку, умноженную на число ( ).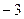

Прибавили к 4-й строке 1-ю строку, умноженную на число ( ).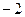

Прибавили к 5-й строке 1-ю строку, умноженную на число ( ).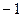

3. Прибавили 2-ю строку к 3-й строке.

Прибавили 2-ю строку к 4-й строке.

~ ~ ~

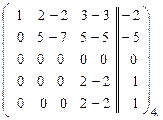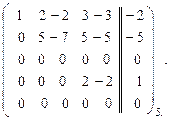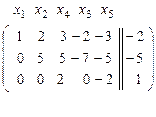
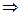
4. Прибавили к 5-й строке 4-ю строку, умноженную на число ( ).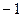

5. Отбросили 3-ю и 5-ю нулевые строки (они эквивалентны равенству ).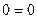

Переставили местами 3-й и 4-й столбцы и над столбцами написали соответствующие

неизвестные.

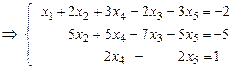- система треугольного вида.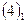

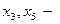свободные неизвестные, 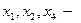базисные неизвестные.

Положим 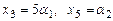, где 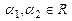. Из 3-го, 2-го, 1-го уравнений системы 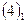последовательно находим неизвестные .

.

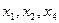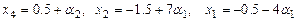Ответ. Система 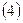совместна, и ее общее решение представимо в ви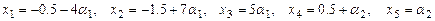де

, где .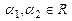

Пример 4. Найти методом Гаусса общее решение системы .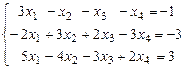

Решение.

~ ~ ~

~ .

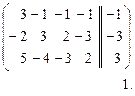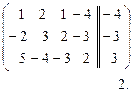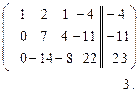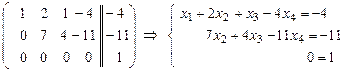1. Прибавили 2-ю строку к 1-й строке.

2. Прибавили ко 2-й строке 1-ю строку, умноженную на 2.

Прибавили к 3-й строке 1-ю строку, умноженную на ( ).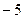

3. Прибавили к 3-й строке 2-ю строку, умноженную на 2.

Наличие в полученной системе невыполнимого равенства 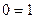означает несовместность заданной системы уравнений.

___________________

Домашнее задание.

Решить методом Гаусса следующие системы (или доказать несовместность):

1) 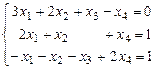; 2) 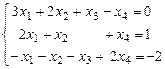.