Метод узловых потенциалов

Метод узловых потенциалов

За неизвестные вметоде узловых потенциалов принимаютсяпотенциалы узлов φ_k. Если мы узнаем потенциалы всех узлов цепи, то затем уже легко сможем определить ток в любой ветви между узлами «k» и «n» из обобщенного закона Ома:

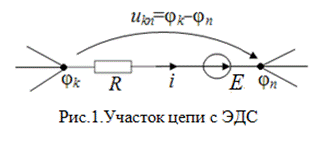iR= E+ (φ_k− φ_n) (1)

(знаки слагаемых здесь соответствуют стрелкам тока и ЭДС на рис. 1).

Пусть цепь имеет N узлов. Один узел мы всегда можем заземлить, положив его потенциал φ = 0. Следовательно, неизвестными в этом методе остаются (N−1) величин φ_k. Значит, метод узловых потенциалов приводит всего лишь к (N−1) алгебраическим уравнениям, т. е. сколько дает лишь 1-е правило Кирхгофа.

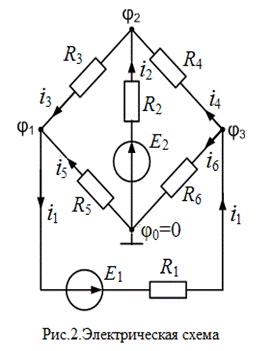
Рассмотрим работу этого метода на примере цепи, показной на рис. 2 (мостовая схема). Она имеет четыре узла и три независимых контура. Прямое использование правил Кирхгофа привело бы здесь к 3+3=6 уравнениям относительно неизвестных токов в ветвях. Метод узловых потенциалов приводит лишь к трем уравнениям.

Заземлим, например, узел 0, положив φ₀ = 0, и определим потенциалы узлов φ₁, φ₂ и φ₃. Расставим произвольно стрелки токов i_k в ветвях (k= 1, 2, …,6) и запишем первые уравнения Кирхгофа для узлов 1, 2 и 3:

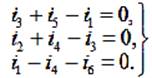(2)

Теперь выразим эти токи из обобщенного закона Ома (1) с учетом правила знаков:

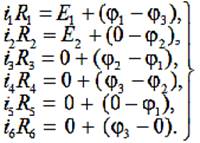(3)

Подставив найденные отсюда токи i₁, i₂,…,i₆ в (2), получим систему трех уравнений относительно неизвестных потенциалов φ₁, φ₂ и φ₃:

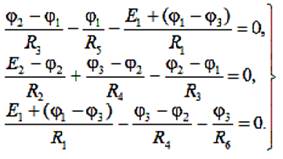
Определив из этой системы потенциалы узлов φ₁, φ₂ и φ₃ и подставив их в (3), находим все токи i₁, i₂, …, i₆ с их знаками относительно выбранных на рис. 2 стрелок.

Метод контурных токов

Если цепь имеет N узлов и К независимых контуров, то для расчета токов на всех участках такой цепи правила Кирхгофа дают (N−1)+К уравнений. Метод узловых потенциалов позволяет обойтись системой лишь (N−1) уравнений, т. е. сколько дает первое правило Кирхгофа. Метод контурных токов приводит к К уравнениям, т. е. сколько дает лишь второе правило Кирхгофа. Этот метод состоит в следующем.

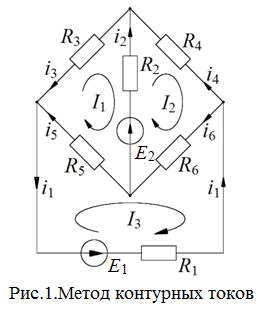Пусть цепь имеет К независимых контуров. Каждому из них ставится в соответствие некоторый ток I_n (n= 1, 2, …, К), постоянный вдоль всего контура. Такие токи называютсяконтурными. Удобно все контурные токи направлять одинаково, скажем, по часовой стрелке. Рассмотрим, для определенности, мостовую схему, что на рис. 1. Она имеет три независимых контура (выберем их простыми), следовательно, в ней задаются три контурных тока: I₁, I₂, I₃ (рис.5). При одинаковом направлении контурных токов, истинные токив смежных ветвях (i₂, i₅ и i₆) будут равны разностям двух соседних контурных токов, а в ветвях, не являющихся смежными, истинныетоки(i₁, i₃ и i₄) будут совпадать с контурными.

Для изображенной на рис. 1 схемы второе правило Кирхгофа для контурных токов дает:

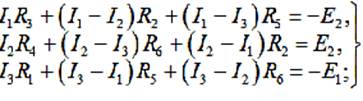
или:

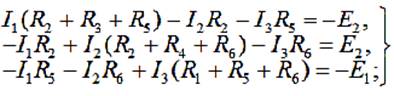
Решая эту систему уравнений, получим три неизвестных контурных тока :I₁, I₂ и I₃. Затем определяем истинные токи в ветвях с их знаками относительно выбранных стрелок:

i₁ = − I₃, i₂ = I₂ − I₁,

i₃ = −I₁, i₄ = −I₂,

i₅ = I₁ − I₃, i₆ = I₂ − I₃.

Следует отметить, что в методе контурных токов первое правило Кирхгофа выполняется автоматически, в силу самой идеи метода. Действительно, например, для представленной на рис. 1 схемы:

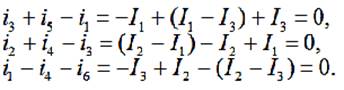
Выбор того или иного метода расчета зависит от конкретного графа(сетки) электрической цепи: если граф таков, что в нем много контуров, но мало узлов, то удобно пользоваться методом узловых потенциалов, в противном случае – методом контурных токов.

МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ

При расчете электрической цепи методом узловых потенциалов определяются потенциалы узлов цепи, а затем по закону Ома токи в ее ветвях. Метод целесообразно применять в тех случаях, когда число узлов цели меньше или равно числу независимых контуров этой цепи.
Так, для электрической цепи, имеющей четыре узла, составляется три расчетных уравнения (например, для узлов 1, 2 к 3 потенциал узла 4 принимается равным нулю):

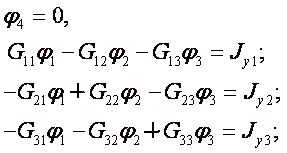
где φk - искомый потенциал K-го узла цепи (K = 1,2, 3)
Gkk- (G11, например) собственная (узловая) проводимость k-го узла, равная сумме проводимостей всех ветвей, присоединенных к этому узлу;
Gkm -(G12, например) взаимная (межузловая) проводимость узлов k и m, равная суше проводимостей ветвей, включенных непосредственно между этими узлами;
Jyk (Jy1, например) - узловой ток к-го узла, определяемый из выражения

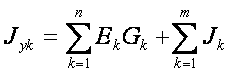
Под знаком первой суммы произведения ЭДС ветвей, присоединенных к К-му узлу, на проводимости этих ветвей учитывается ЭДС с положительным (отрицательным) знаком, если она направлена к К-му узлу (от К-го узла). Под знаком второй суммы со знаком «+» ("-"} учитываются токи источников тока, которые направлены к К-му узлу (от К-го узла).
Если в цепи между двумя узлами включен идеальный источник ЭДС (внутреннее сопротивление которого равно нулю), необходимо принимать равным нулю потенциал одного из его зажимов, тогда потенциал другого зажима источника будет равен ЭДС с
соответствующим знаком, а количество расчетных уравнений сократится.
Последовательность расчета цепи методом узловых, потенциалов рас-
смотрим на примере. Параметры цепи считаются заданными.

ПРИМЕР 1: Определить токи в ветвях цепи (рис. 1) методом
узловых потенциалов. Положительные направления токов принять по рисунку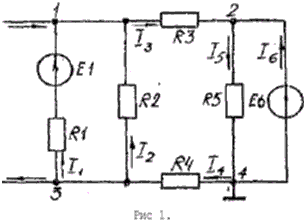

E1=100В R1=10 Ом
E6=200В R2=20 Ом
I=5А R3 =5 Ом R4=25 Ом R5=40 Ом

1. В заданной цепи четыре узла. Приравняем нулю (заземлим) потенциал узла 4.Тогда ф4=0

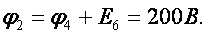
2. Составим расчетную систему уравнений для узлов, потенциалы которых подлежат определению:

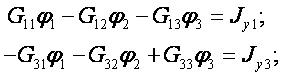
Для узлов 2 и 4 уравнения не составляются, так как потенциалы этих узлов известны.
3. Определим узловые и межузловые проводимости:

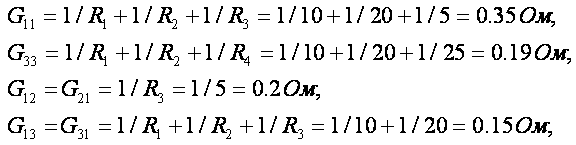
Взаимная проводимость между узлами 2 и 3 равна нулю, так как эти узлы непосредственно не связаны между собой какими-либо ветвями» т.е. G23=G32=0. Проводимость ветви с источником тока J также равна нулю, так как его внутреннее сопротивление бесконечно велико. Если в какой-либо ветви последовательно включено несколько резисторов, вначале определяется общее сопротивление этой ветви, а затем ее проводимость.
Определим узловые токи:

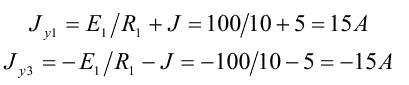
4. Подставим полученные значения узловых и межузловых проводимостей, а также узловых токов в расчетную систему уравнений. Решая ее, определим искомые потенциалы узлов цепи:

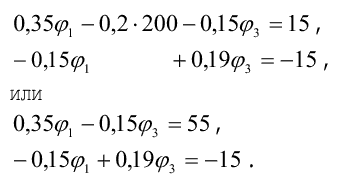
Решить систему уравнений можно методом определителей или с помощью микрокалькулятора по соответствующей программе, однако, если система содержит два уравнения, ее целесообразно решать домножением на общие множители:

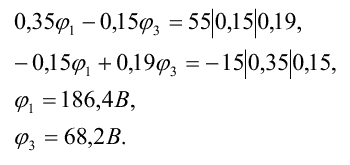
*Запись выше несколько непонятна. Она означает домножение левой и правой частей уравнения на множители. Вообще необходимо любым способом решить систему уравнений: например, подстановкой.

Для проверки расчета целесообразно полученные значения потенциалов, вычисленные с точностью до 3-4 значащей цифры, подставить в исходную систему уравнений, которые при этом, очевидно, должны обратиться в тождества.
5. Используя закон Ома, определим токи в ветвях цепи.
Направления токов в ветвях выбраны произвольно и указаны на схеме (рис. I).
Составим выражение для разности потенциалов (напряжения) между узлами 3 и 1:

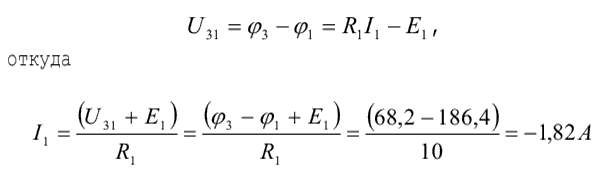
т.е. в дальнейшем при выбранном направлении тока в ветви его величина определяется следующим образом: в числителе выражения от потенциала узла, из которого ток вытекает, вычитается потенциал узла, к которому ток подтекает.
Если в ветви есть ЭДС, она учитывается со знаком «+» ("-"), когда ее направление совпадает (противоположно) с направлением тока, В знаменателе выражения для тока находится суммарное сопротивление ветви. Аналогично определяются токи остальных ветвей:

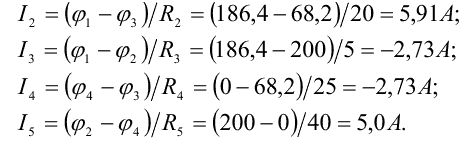
Значения токов I1 , I2, и I4 получились со знаком «-». Это свидетельствует о том, что их направления в ветвях противоположны выбранным. Токи I3 и I4 равны между собой в силу принципа непрерывности электрического тока.
Ток в ветви с идеальной ЭДС Е6 определяется из уравнения, составленного по первому закону Кирхгофа. Например, для узла 2

6. Проверка расчета цепи выполняется по законам Кирхгофа
и уравнению энергетического баланса (балансу мощностей),
по первому закону Кирхгофа алгебраическая сумма токов в любом узле электрической цепи равна нулю. Проверяем выполнение этого закона для всех узлов цепи (кроме узла 2: из уравнения для этого узла определялся ток I6:

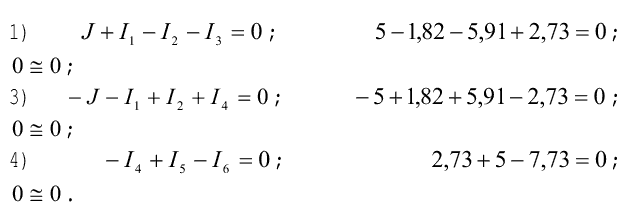
По второму закону Кирхгофа алгебраическая сумма ЭДС в любом замкнутом контуре электрической цепи равна алгебраической сумме падений напряжений на элементах этого контура. Проверяем выполнение этого закона дня всех независимых контуров заданной цепи;
Для контура с элементами Е1, R1 и R2

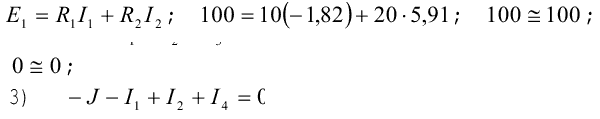
для контура с элементами R2, R3, R4 и R5

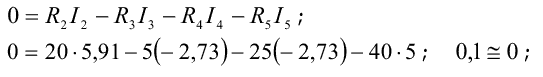
для контура с элементами E1, R3, E6, R4 и R1

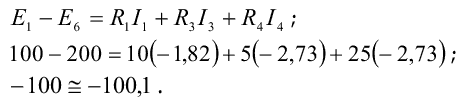
Дня любой электрической цепи мощность, потребляемая резисторами этой цепи, должна равняться мощности источников энергии. Уравнение энергетического баланса ( баланс мощностей) в общем виде записывается следующим образом:

В левой части уравнения учтена мощность источников энергии. Мощность источников ЭДС учитывается с положительным (отрицательным) знаком, если ток, протекающий через источник ЭДС, совпадает ( противоположен) с направлением ЭДС.
Для определения знака мощности источника тока необходимо определить напряжение на источнике. Если ток источника вытекает из точки с меньшим потенциалом и подтекает к точке с большим потенциалом, мощность источника будет положительной (источник генерирует энергию). Если ток источника вытекает из точки более высокого потенциала по сравнению с потенциалом точки, куда ток втекает, мощность источника будет отрицательной, а режим его работы соответствует потреблению энергии.
В правой части уравнения энергетического баланса записывается арифметическая сумма мощностей, потребляемых резисторами цепи и определяемых по закону Джоуля-Ленца. По своему физическому смыслу эти мощности могут быть только положительными.
Для заданной электрической цепи (рис. I) уравнение энергетического баланса имеет вид

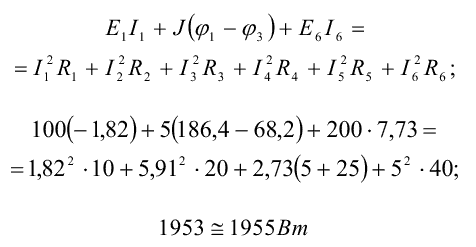
Расчет считается выполненным правильно, если расхождение между левой и правой частями уравнения электрического баланса не превышает 1...2%. Следует помнить, что при выполнении проверки расчета по законам Кирхгофа и балансу мощностей уравнения составляются по выбранным. В начале расчета положительным направлениям токов в ветвях заданной цепи, а числовые значения токов в уравнения подставляются со знаками, полученными в расчете.