Розв'язування економічних задач.

Нехай задано функцію z = f(x, y).

Означення. Частинною еластичністю функції f відносно хназивається величина

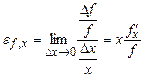. (12)

Частинною еластичністю функції f відносно уназивається величина

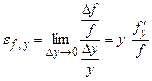. (13)

Інтерпретація. :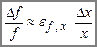

Відсоткове відношення функції наближено дорівнює відсотковому відношенню змінної х з коефіцієнтом 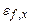(коли у — величина стала).

Найчастіше в економіці застосовують поняття еластичності попиту.

Нехай функції q₁ = f₁(p₁, p₂) i q₂ = f₂(p₁, p₂) виражають попит на товари А і В, що залежать від цін р₁ і р₂ на зазначені товари. Частинні еластичності попиту щодо цін р₁ і р₂ за формулами (12) і (13) набирають вигляду:

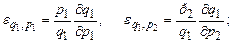
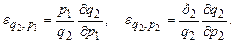
Інтерпретація. Частинна еластичність 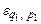попиту на товар А щодо ціни р₁ цього товару наближено подає відсоток підвищення (або зниження) попиту на товар А, якщо його ціна зростає на 1%, а ціна товару В лишається незмінною.

Частинна еластичність 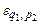попиту на товар А щодо ціни товару В наближено подає відсоток підвищення (зниження) попиту на товар А, якщо ціна товару В зростає на 1%, а товару А залишається без змін.

Приклад. Функція попиту на товар А подається у вигляді

.

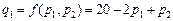Знайти частинні коефіцієнти еластичностей.

●Маємо

.

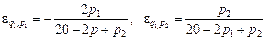Для цін р₁ = 2, р₂ = 4

.

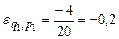Це означає, що коли ціна товару А зростає на 1%, а товару В залишається без змін, то попит на товар знижується на 0,2%. Рівність

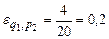
відбиває аналогічну залежність: якщо ціна товару В зростає на 1% за незмінної ціни товару А, то попит на цей товар зростає приблизно на 0,2%.◄

Економічна задача, що приводить до частинних похідних

Функцією 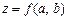подається залежність обсягу виробництва від факторів А і В, кількість яких становить відповідно а та b одиниць.

Припустимо, що кількість фактора А зростає, тоді як кількість фактора В лишається незмінною.

Відповідно приріст обсягу випуску продукції подається різницею 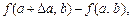а відношення цього приросту до приросту кількості фактора А набирає вигляду:

.

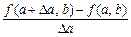Якщ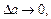о маємо

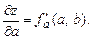
Це гранична продуктивність фактора А. Аналогічно, гранична продуктивність фактора В

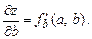
Приклад. Для деякого товару визначено виробничу функцію

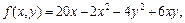
де x, y — фактори виробництва. Знайти граничну продуктивність фактора x.

● Запишемо частинну похідну виробничої функції за змінною x:

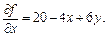
Це і є гранична продуктивність фактора x.◄

Максимізація прибутку від випуску товарів

Нехай виробничі функції кожного з двох продуктів залежать від двох факторів. Сумарна кількість кожного фактора фіксована. За яких умов прибуток буде максимальним, якщо ціни на продукцію відомі?

Позначимо х₁, х₂ — обсяг випуску відповідно першого та другого продукту; х₃, х₄, х₅, х₆ — обсяги факторів, використовуваних для виробництва першого і другого продуктів з відповідною виробничою функцією:

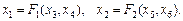
Задано обмеження на кількість факторів

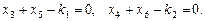
Функція Лагранжа в цьому разі набирає вигляду:

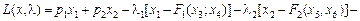
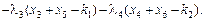
Прирівнюючи частинні похідні за х₁, х₂, х₃, ..., х₆ до нуля, ді-
стаємо:

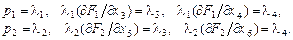
Звідси знаходимо умови, які максимізують прибуток:

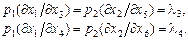
Отже, вартість граничного продукту за кожним фактором буде однаковою в обох галузях. Зауважимо, що всі множники Лагранжа дорівнюють цінам. Якщо розглядається конкурентне ціноутво­рення, то 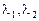— ціни продуктів, а 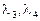— ціни факторів.

Література:

Валєєв К. Г., Джалладова І. А.Вища математика: Навч. посібник: У 2-х ч. — К.: кнеу, 2001. — Ч. 2. — 451 с.